КСКЭР / Л р 1 МКЭ

Нестационарные задачи теории поля

Одним из важных классов физических задач представляют задачи, учитывающие изменение искомых величин во времени. В некоторых из них имеет место так называемый переходный период между началом физического процесса и достижением установившегося состояния. Встречаются задачи, в которых установившееся состояние вообще не достигается и переходный период составляет весь физический процесс.

С нестационарными задачами очень часто сталкиваются при исследовании явления переноса тепла, течения грунтовых вод, а также динамического поведения различных конструкций. В данной лабораторной работе рассматривается задача моделирования распределения температуры в тонком стержне заданной длины и сечения, изготовленного из однородного материала. Дифференциальное уравнение этой задачи имеет вид:

,

где  – коэффициент теплопроводности материала стержня;

Q – источник тепла внутри тела;

с – удельная теплоемкость;

 – плотность материала стержня.

Граничные условия:

1. На части контура стержня задан тепловой поток

где n – координата по внешней нормали к поверхности;

q – плотность теплового потока.

2. На части контура стержня происходит конвективный теплообмен

где h – коэффициент конвекции;

– температура окружающей среды.

Функционал для данной задачи имеет вид:

Минимизация функционала:

Решение задачи методом конечных элементов

Процесс минимизации функционала можно свести к следующей системе дифференциальных уравнений:

(1)

где [С] – матрица демпфирования;

[K] – матрица теплопроводности;

{T} – вектор узловых значений температуры;

{F} – вектор нагрузки.

Для каждого i-го элемента стержня, матрицы и вектора имеют вид:

где A – площадь поперечного сечения стержня;

L – длина i-го элемента стержня;

Заменим первую производную по времени уравнения (1) следующим соотношением

(2)

Так как вычисляется в средней точке интервала , в этой точке также необходимо вычислить и :

(3)

(4)

Подставив выражения (2), (3) и (4) в уравнение (1), получим:

(5)

Введем матрицы:

и

Уравнение (5) примет вид:

(6)

Пример решения задачи методом конечных элементов

Вычислим распределение температуры в однородном стержне со следующими физическими характеристиками:

r=1

=100

h=10

q=5

=40

c=15

t=1

Разобьем стержень на 5 элементов, длиной 10 см каждый.

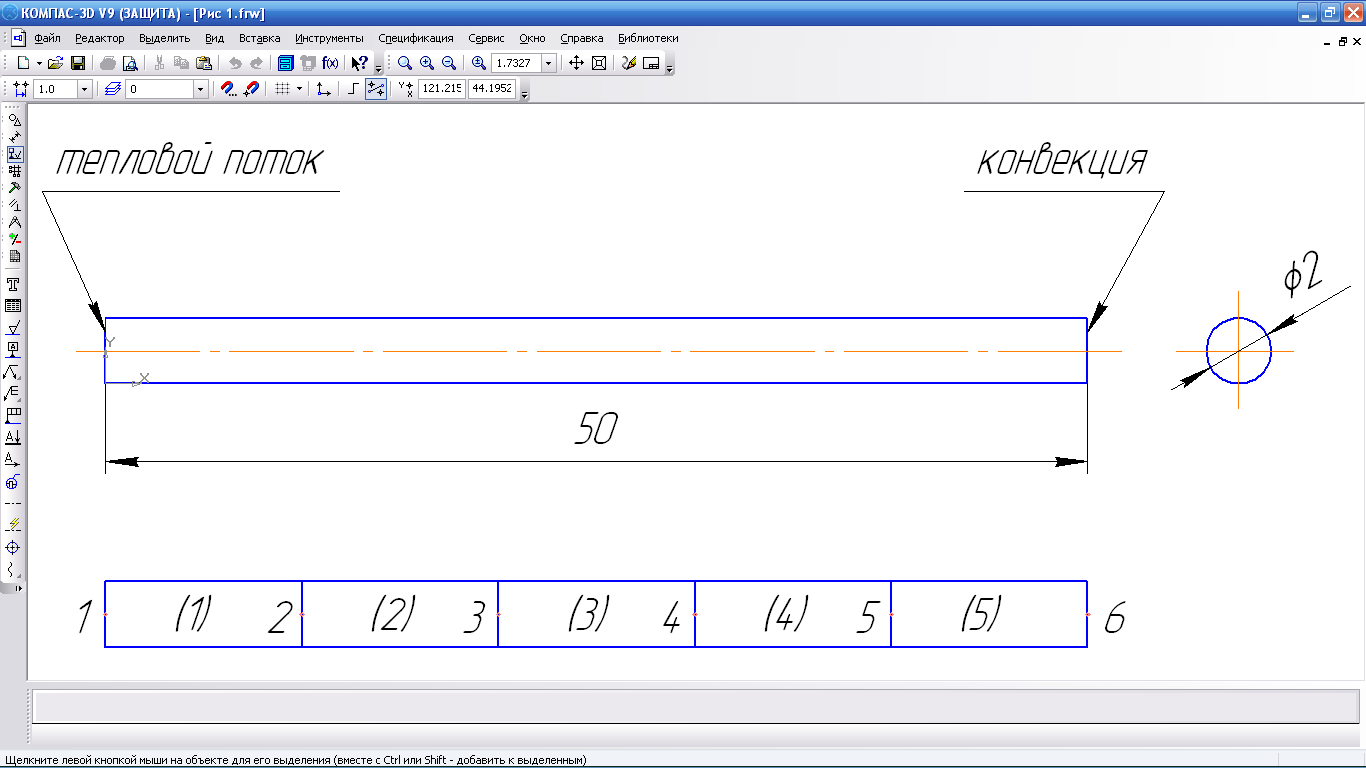
В этом случае:

A=

;

;

, i=2,3,4;

Определим матрицы в уравнениях (5) и (6).

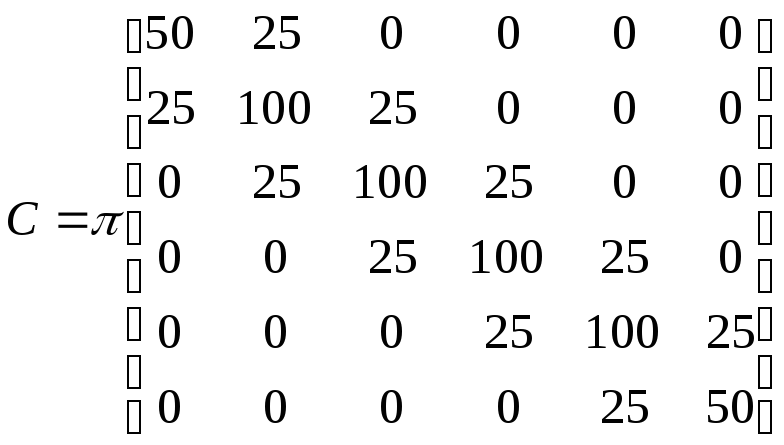
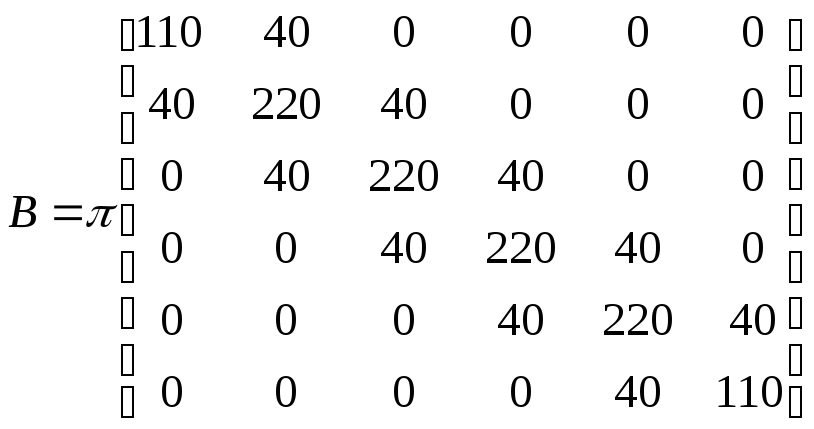
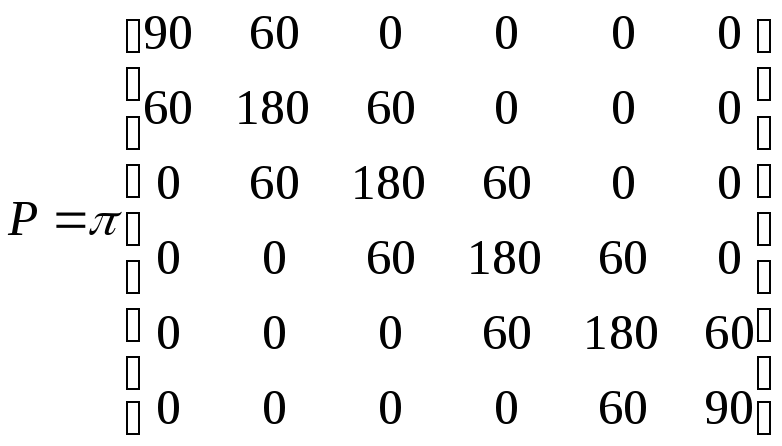
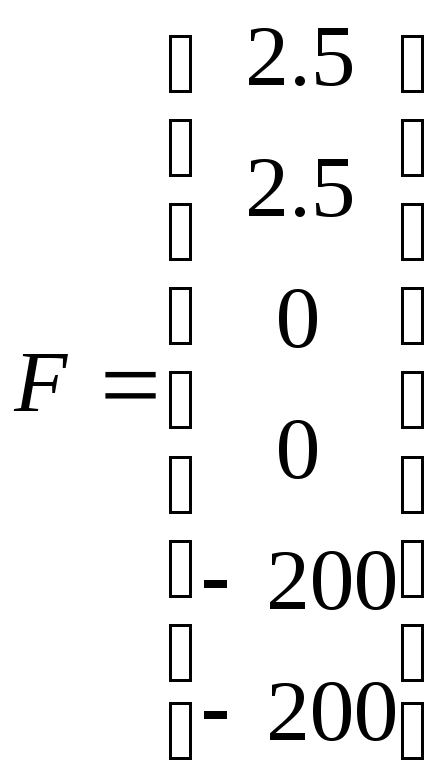
Подставим полученные выражения в уравнение (6) и решим систему для момента времени 1. Для следующего момента времени 2 решим систему (6) ещё раз, при этом , и т. д.