
- •Основные уравнения теории осевых машин
- •II.Уравнение энергии
- •При увеличении кинетической энергии потока газа или жидкости происходит изменение давления и плотности
- •Интеграл может быть вычислен в случае, когда известна зависимость между и Р.
- •тогда теоретическая энергия LT равна:
- •Уравнение энергии абсолютного давления через лопастную решетку можно записать:
- •III. Уравнение количества движений
- •Для несжимаемой жидкости 1 2 и w1a w2a (см. рис.)
- •IV. Уравнение циркуляции
- •Обозначим
- •Напор. Потери энергии и КПД осевых нагнетателей.
- •Теоретический напор, который может вычислен по уравнению Эйлера, при условии U1 U2 U
- •Теоретическое давление, создаваемое рабочим колесом осевого нагнетателя:
- •Эффективность решеток осевых машин для несжимаемой жидкости оценивается КПД решетки:
- •Для несжимаемой жидкости:
- •Теоретическое изменение давления в решетке
- •Раскроем Pa и Pu и подставим в решет
- •Действительное давление развиваемое осевым нагнетателем выражается формулой:
- •В отводе (диффузоре) появляется диффузорный эффект, повышающий давление:
- •Если учесть P как потери давления в подводе и отводе, то давление, создаваемое
- •Механический КПД учитывает потери энергии от трения в уплотнениях, подшипниках и дискового трения
- •Мощность на валу осевого нагнетателя определяется формулой:

Основные уравнения теории осевых машин
Лекция №12 (продолжение лекции №11)

II.Уравнение энергии
Вотносительном движении через рабочее колесо осевой машины энергия потоку не сообщается, происходит лишь преобразование кинетической энергии в потенциальную. Этот процесс сопровождается переходом части энергии в теплоту.

При увеличении кинетической энергии потока газа или жидкости происходит изменение давления и плотности потока и, следовательно, уравнение энергии можно записать:
|
|
|
|
w2 |
|
w2 |
2 dP |
L |
|
|
|
|
|
1 |
2 |
|
|
||
|
|
|
|
2 |
|
2 |
1 |
|
|
где |
w2 |
, |
w2 |
|
|
|
|
|
|
2 |
2 |
кинетическая энергия потока на входе и |
|||||||
|
1 |
|
2 |
|
|
|
|
|
|
выходе соответственно; Р давление потока;плотность потока;
ΔL энергия, переходящая в теплоту.

Интеграл может быть вычислен в случае, когда известна зависимость между и Р.
В осевых машинах низкого давления (вентиляторах) процесс сжатия изотермический. Температура перемещаемого газа почти не изменяется.
В осевых компрессорах процесс сжатия
политропный.
Энергия, сообщаемая потоку лопастной решеткой, может быть рассчитана по основному уравнению центробежной машины, в котором:
U1 U2 U

тогда теоретическая энергия LT равна:
LT U (C2U C1U ) U CU
Из параллелограмма скоростей (см. предыд.
лекцию) следует:
C1U U1 C1a ctg 1
C2U U2 C2a ctg 2
Тогда: LT UCa (ctg 1 ctg 2 )
LT энергия, сообщаемая газу рабочим колесом.

Уравнение энергии абсолютного давления через лопастную решетку можно записать:
U C |
(ctg ctg |
) C |
|
(T |
T ) |
C2 |
C2 |
|
p |
2 |
1 q |
||||||
a |
1 |
2 |
|
2 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
где СР изобарная теплоемкость.

III. Уравнение количества движений
Служит для расчета сил взаимодействия между потоком и лопастями осевой машины.
Участок лопасти r действует на поток с силой Р
(см. рис.)
P Pa PU
где Ра проекция силы Р на ось нагнетателя; РU проекция силы Р на ось решетки.

|
|
|
|
|
Если |
Р1 и |
Р2 |
— |
давления |
|
|
|
|
|
|
соответственно в сечениях 1–1 |
|||||
|
|
|
|
|
и 2-2, |
|
|
|
|
|
|
|
|
|
|
|
rtw1a 1 |
|
— масса, |
||
|
|
|
|
|
проходящая |
в |
одну |
|
секунду |
|
|
|
|
|
|
через сечение 1–1, |
|
|
|||
то Ра выражается формулой |
|
|
|
|
|
|||||
P rt( p |
2 |
p ) rt( w2 |
|
w2 ) |
||||||
a |
|
|
|
1 |
1 |
1a |
|
|
2 2a |
|
где |
|
t |
– шаг лопастей, |
|
|
|
|
|
||
|
1 |
, 2 |
– плотности жидкости на входе и выходе |
|||||||
соответственно.

Для несжимаемой жидкости 1 2 и w1a w2a (см. рис.)
Pa r t ( p2 p1 )
В этом случае решетка профилей не изменяет осевой скорости потока, и осевая сила, приложенная к потоку, расходуется на повышение давления.
Для компрессорных машин 1 2 .

IV. Уравнение циркуляции
Выражение для циркуляции
Г (w1U w2U )t,
т.к. w1U и w2U — const.
|
V. Теорема Жуковского |
|
|
||
При |
длине |
лопасти, |
равной |
единице |
|
(относительная длина) и при условии 1 |
2 |
, |
|||
подъемная сила лопасти решетки: |
|
|
|
||
Py 
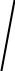 Pu2 Pa2
Pu2 Pa2
Используя формулы для Pu и Pa , получим:
Py Г |
w |
|
w |
2 |
2 |
|
|
1u |
2 |
2u |
w0 |
||
|
|
|
|
|
|
|
