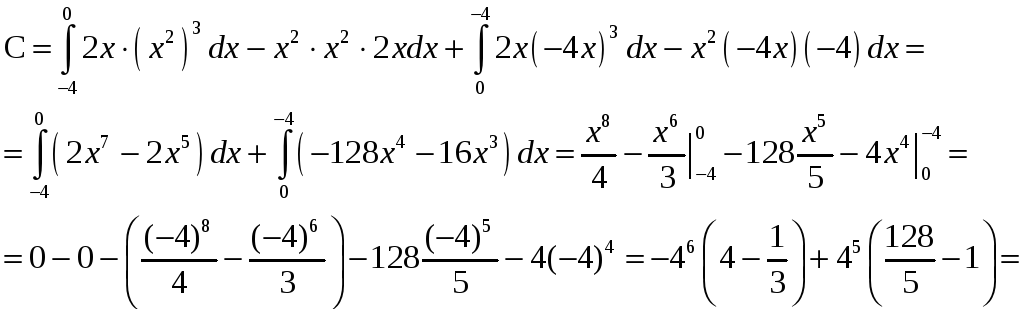- •Раздел 1. Кратные, криволинейные и поверхностные интегралы
- •Раздел 2. Элементы теории поля
- •Раздел 3. Теория функций комплексной переменной
- •Вычислить.
- •Раздел 4. Операционное исчисление
- •Решение типовых заданий
- •6. Проверить потенциальность и соленоидальность векторного поля
- •7. Вычислить
- •10. Вычислить производную аналитической функции в точке
- •11. Решить задачу Коши операционным методом.
- •13. Найти изображение для оригинала .
- •14. Восстановить оригинал по его изображению
- •Литература
Типовые задания, решения вариантов типовых заданий и литература
для самостоятельной подготовки к экзамену (зачету, тесту) по
математике, 3 семестр для студентов заочной (сокращенной) формы
обучения инженерно-технических специальностей
Раздел 1. Кратные, криволинейные и поверхностные интегралы
-
Вычислить площадь плоской области
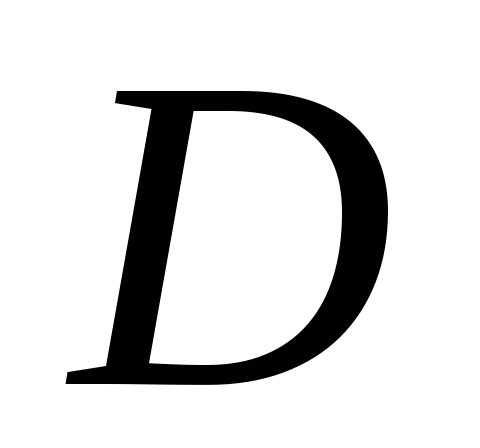 ,
ограниченной данными линиями. Построить
область
,
ограниченной данными линиями. Построить
область
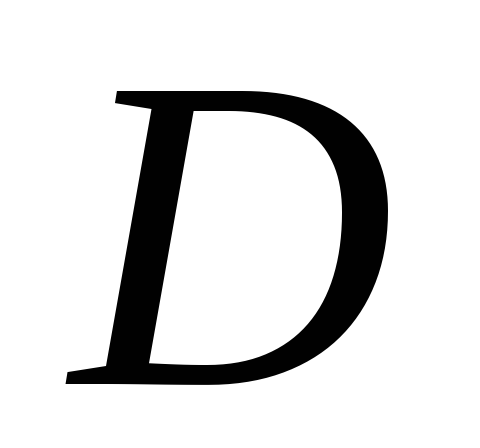 .
.
1.1.
![]() 1.2.
1.2.
![]() 1.3.
1.3.
![]()
1.4.
![]() 1.5.
1.5.
![]()
-
Найти работу (циркуляцию) силы
 при
перемещении вдоль линии
при
перемещении вдоль линии
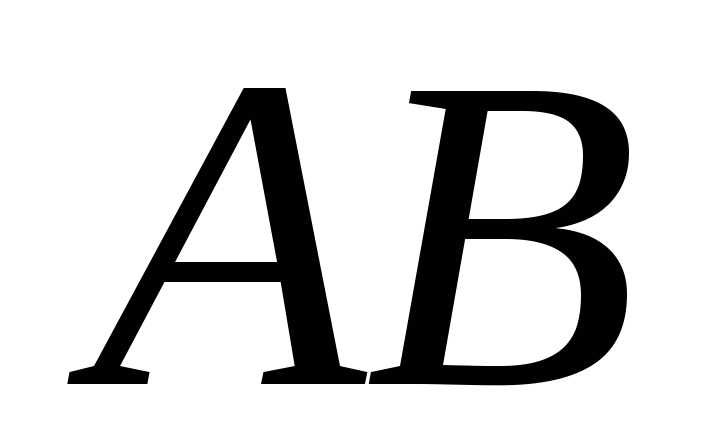 (контура
(контура
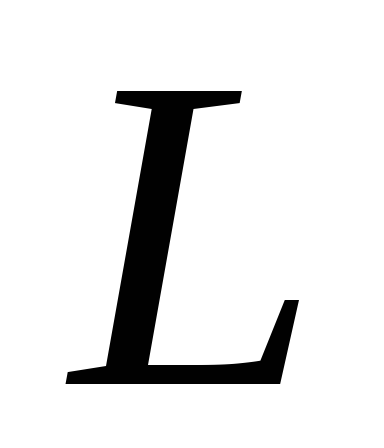 )
от точки
)
от точки
 к точке
к точке
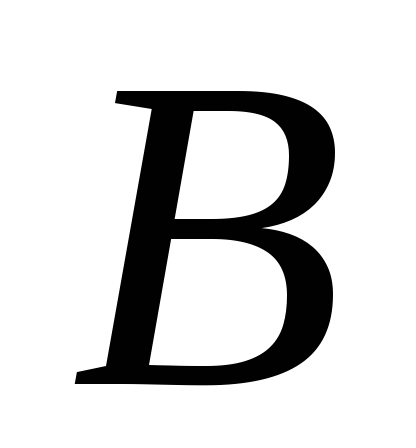 .
.
2.1.![]()
2.2.
![]()
2.3.
![]()
2.4.
![]()
2.5.
![]()
Раздел 2. Элементы теории поля
-
Проверить потенциальность и соленоидальность векторного поля
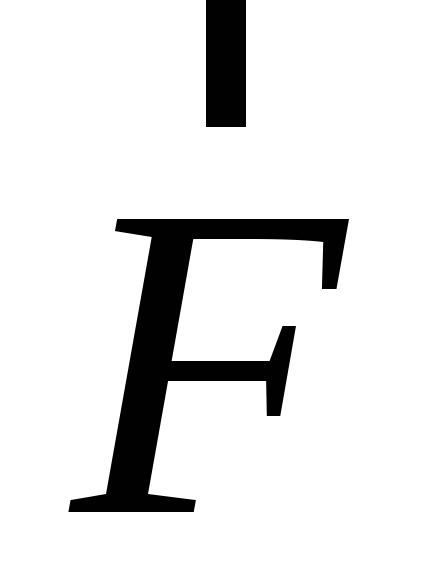 .
.
3.1.![]() 3.2.
3.2.
![]()
3.3.
![]() 3.4.
3.4.
![]()
3.5.
![]()
Раздел 3. Теория функций комплексной переменной
-
Вычислить
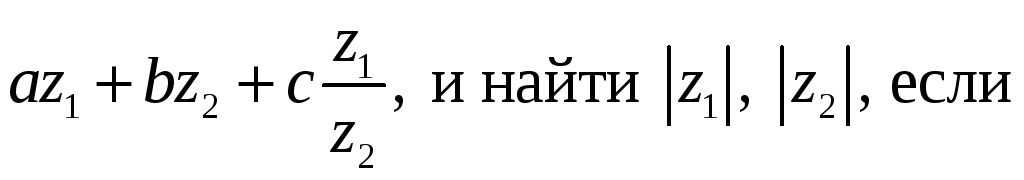
4.1.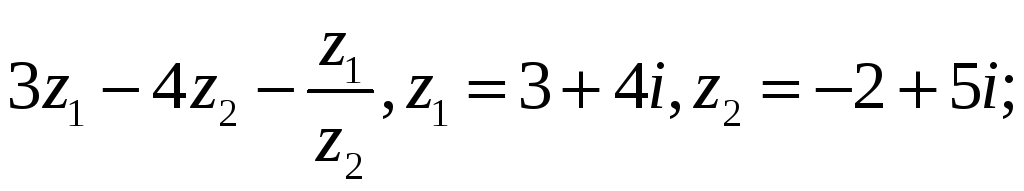 4.2.
4.2.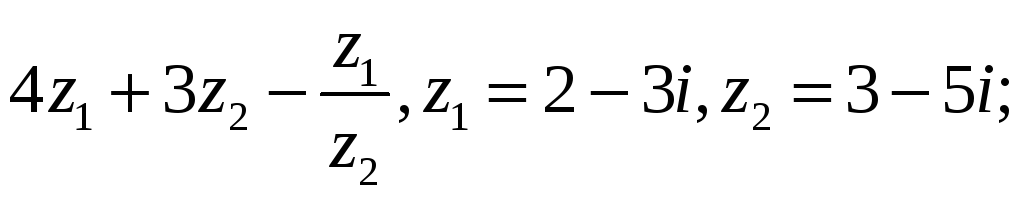
4.3.
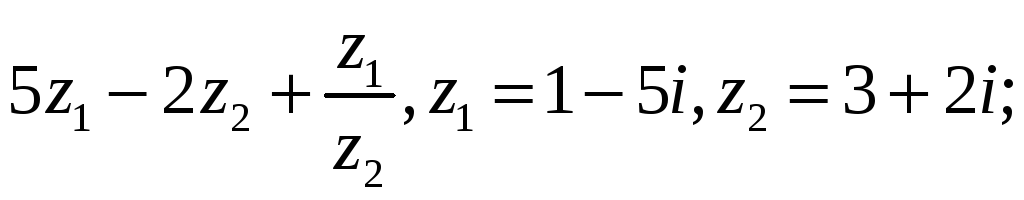 4.4.
4.4.
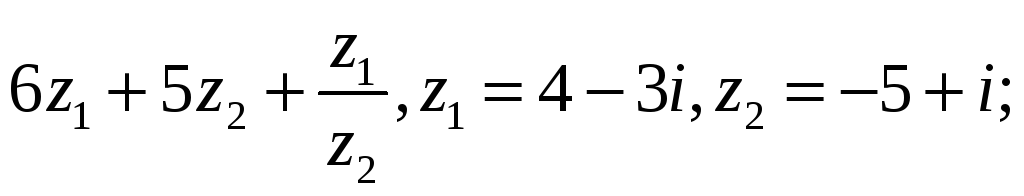
4.5.
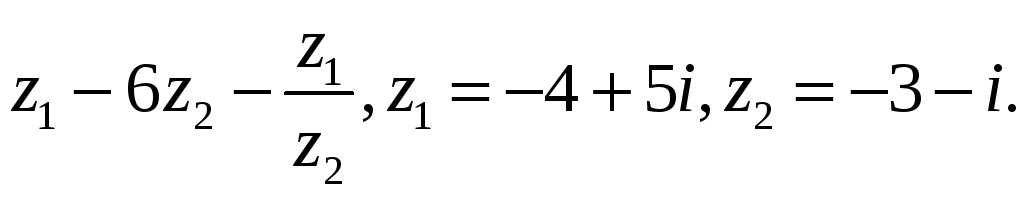
-
Вычислить интеграл, используя основную теорему теории вычетов. Построить контур интегрирования.
5.1. 5.2.
5.2.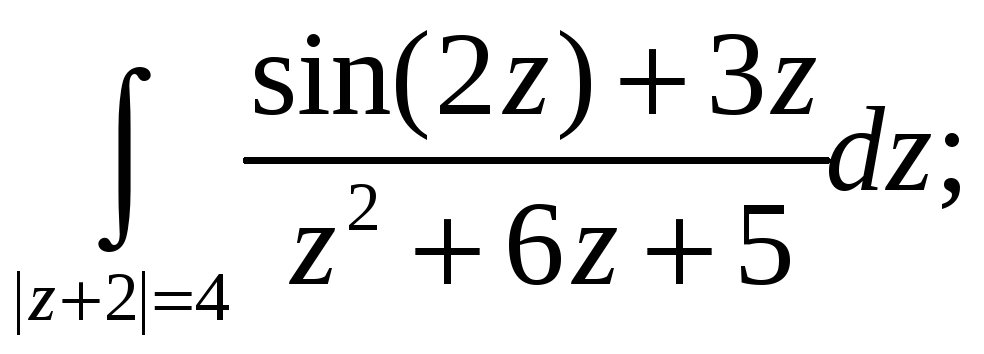 5.3.
5.3.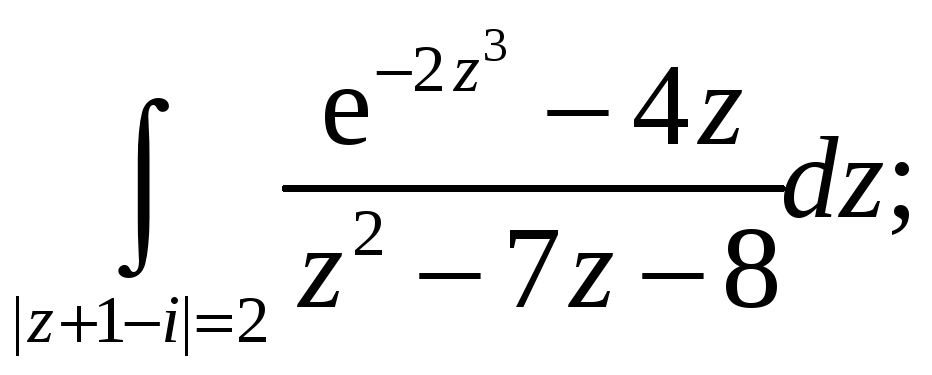
5.4.
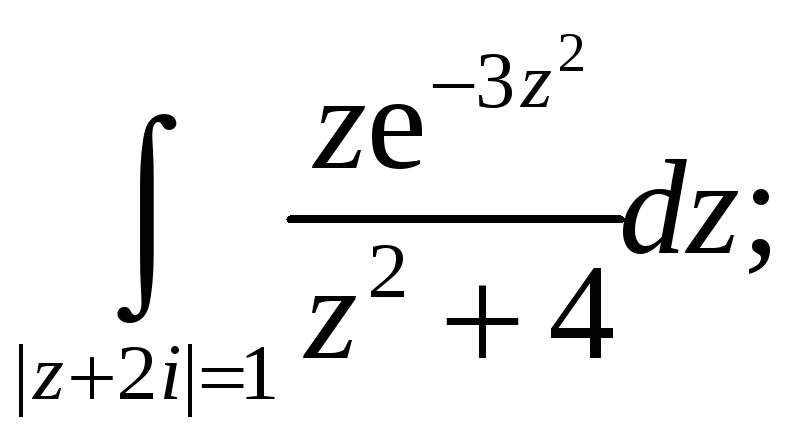 5.5.
5.5.
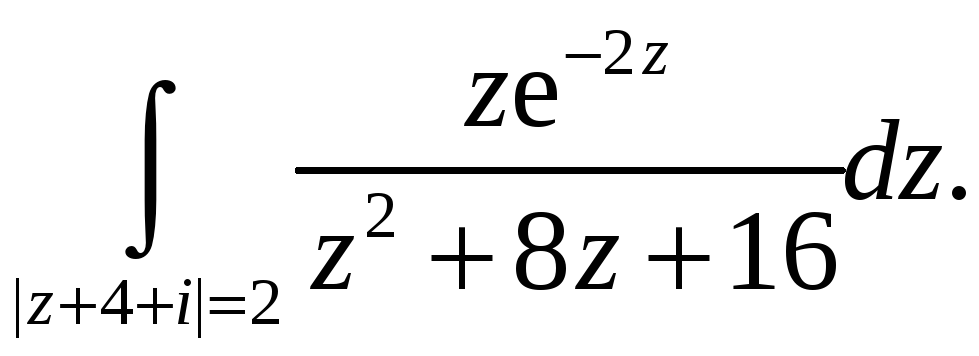
-
Вычислить производную аналитической функции
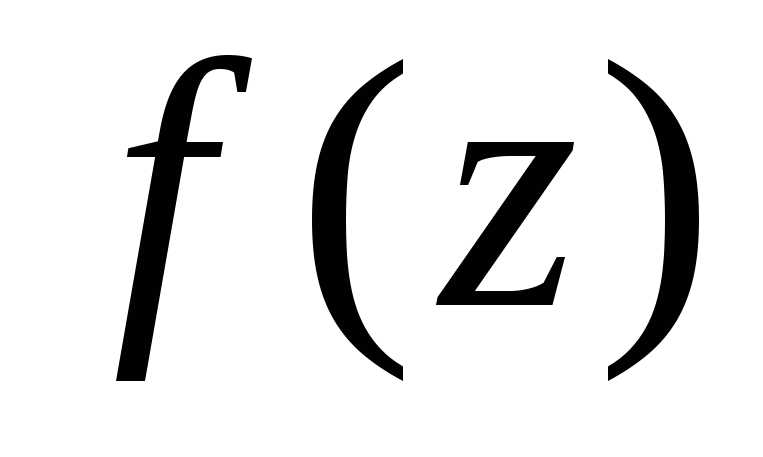 в точке
в точке
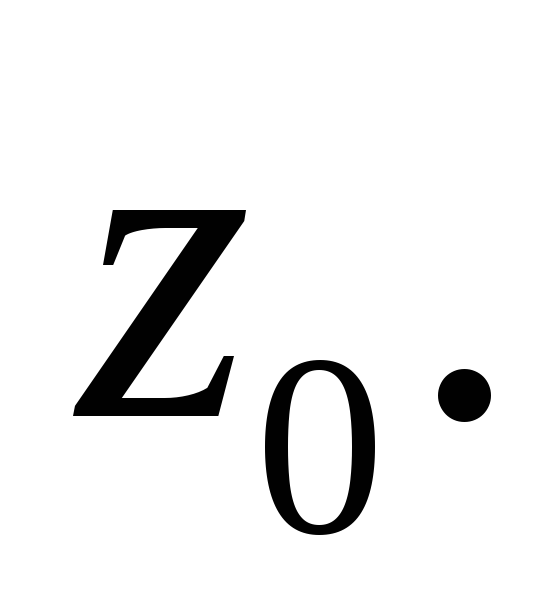
6.1.![]() 6.2.
6.2.
![]()
6.3.
![]() 6.4.
6.4.

6.5.
![]()
-
Вычислить.
7.1.![]() 7.2.
7.2.![]() 7.3.
7.3.![]() 7.4.
7.4.![]() 7.5.
7.5.![]()
Раздел 4. Операционное исчисление
-
Решить задачу Коши операционным методом.
8.1.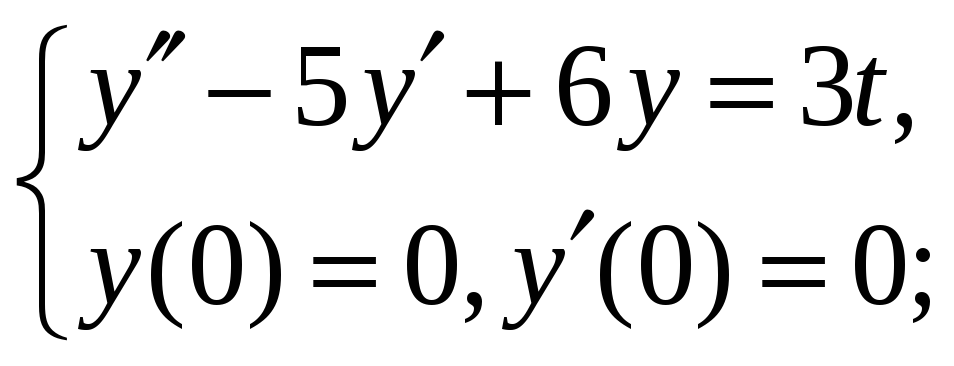 8.2.
8.2.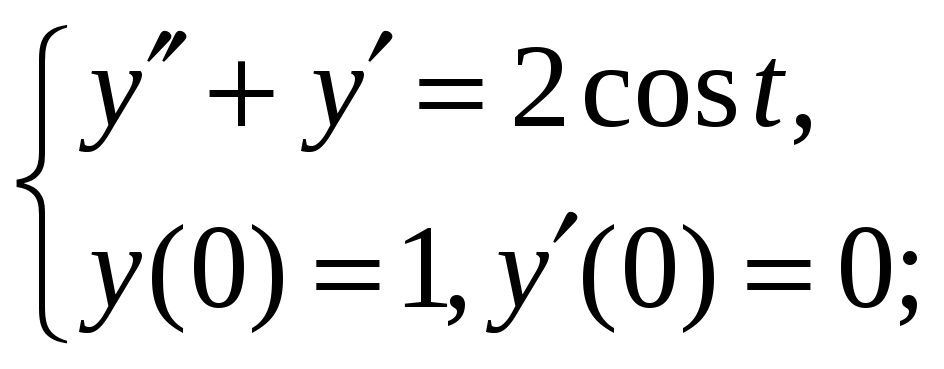 8.3.
8.3.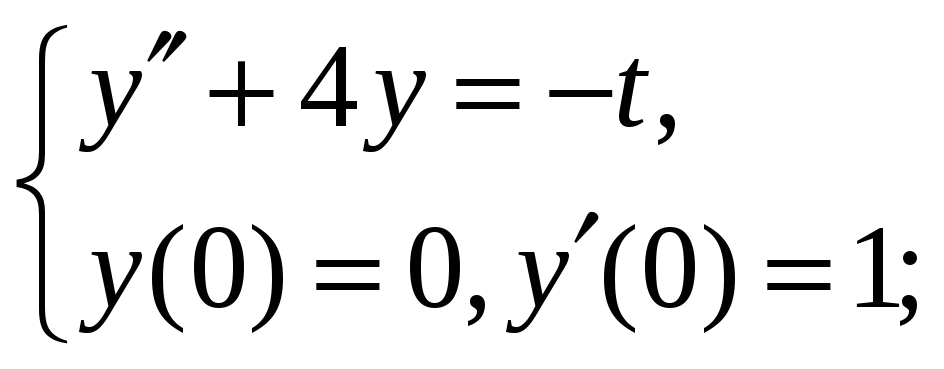
8.4.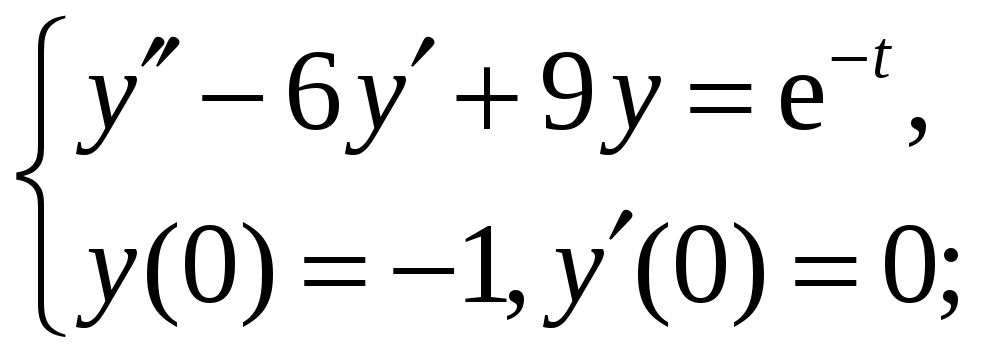 8.5.
8.5.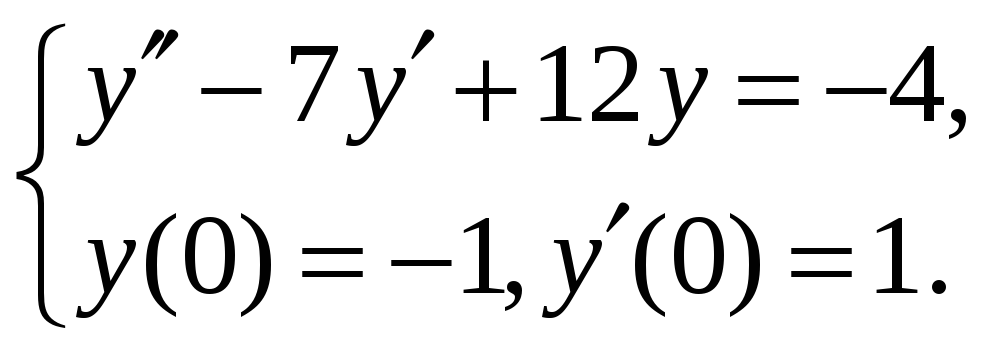
-
Найти изображение
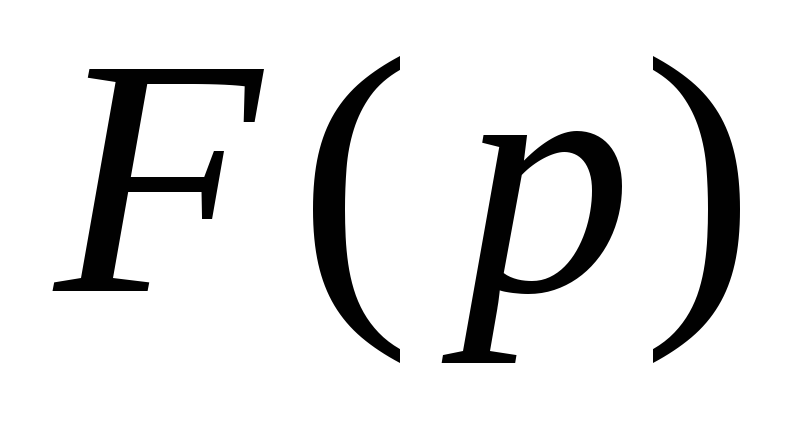 для
оригинала
для
оригинала
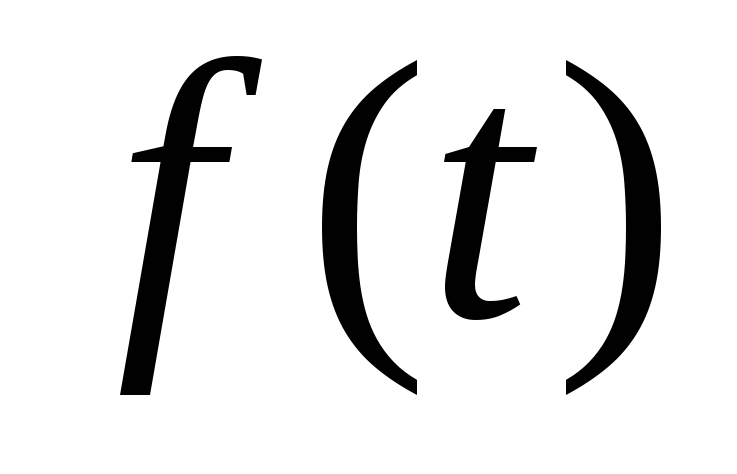 .
.
9.1.![]() 9.2.
9.2.![]() 9.3.
9.3.![]()
9.4.![]() 9.5.
9.5.![]()
-
Восстановить оригинал
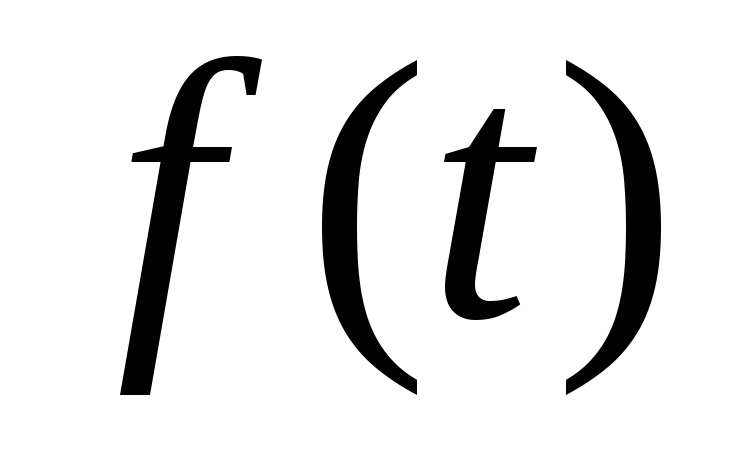 по его
изображению
по его
изображению
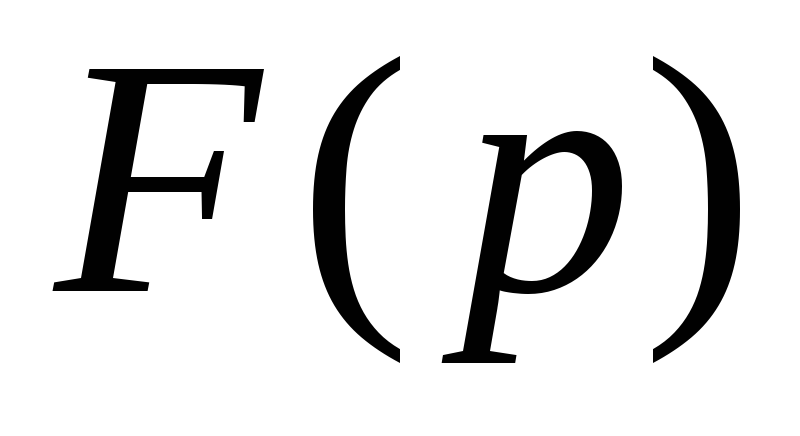 .
.
10.1.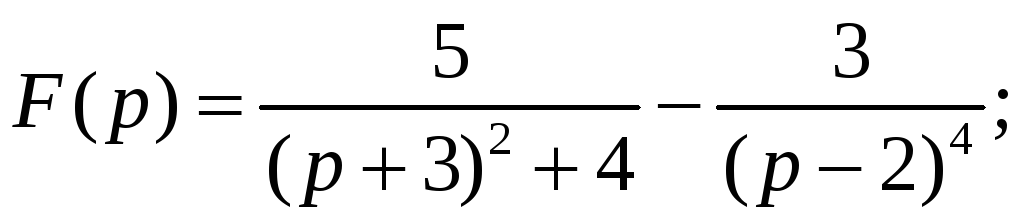 10.2.
10.2.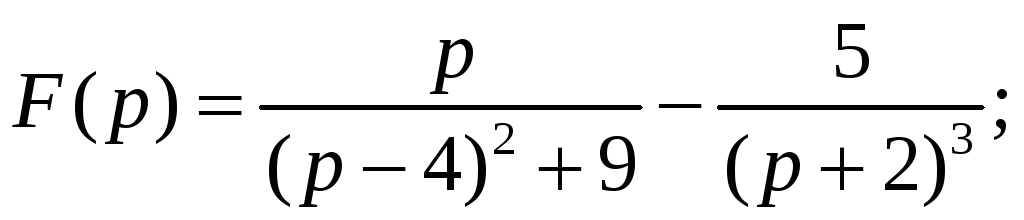
10.3.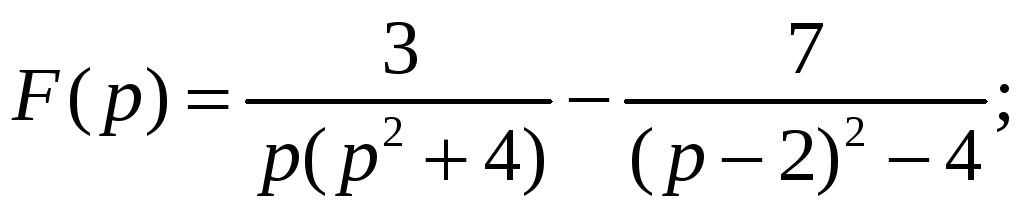 10.4.
10.4.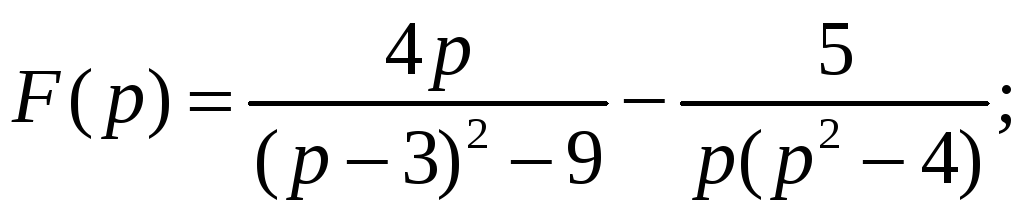
10.5.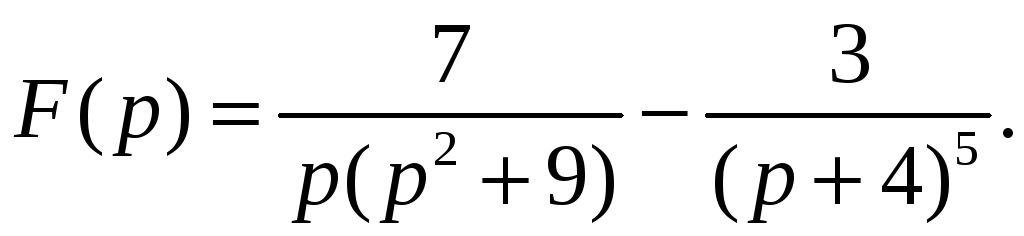
Решение типовых заданий
Типовые задания 1–10 предназначены для студентов заочной (сокращенной)
формы обучения инженерно-технических специальностей.
При решении типовых заданий 1–10 студенты должны использовать методические пособия [1]–[8].
1.
Вычислить
площадь плоской области
![]() ,
ограниченной линиями
,
ограниченной линиями
![]() .
Построить область
.
Построить область
![]() .
.
Р ешение.
Строим график функции
ешение.
Строим график функции
![]() (прямая). Находим:
(прямая). Находим:
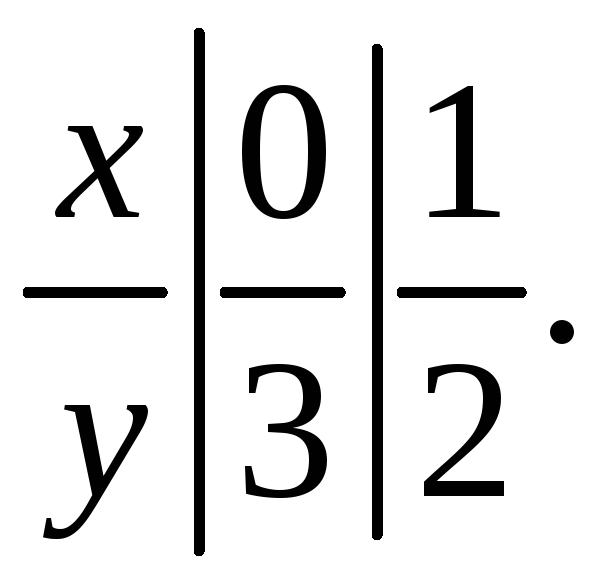 Строим
график функции
Строим
график функции
![]() (парабола). Находим
нули параболы:
(парабола). Находим
нули параболы:
![]() Так как
Так как
![]() ,
то ветви параболы направлены вверх
(рис. 1). Находим точки пересечения
графиков функций:
,
то ветви параболы направлены вверх
(рис. 1). Находим точки пересечения
графиков функций:
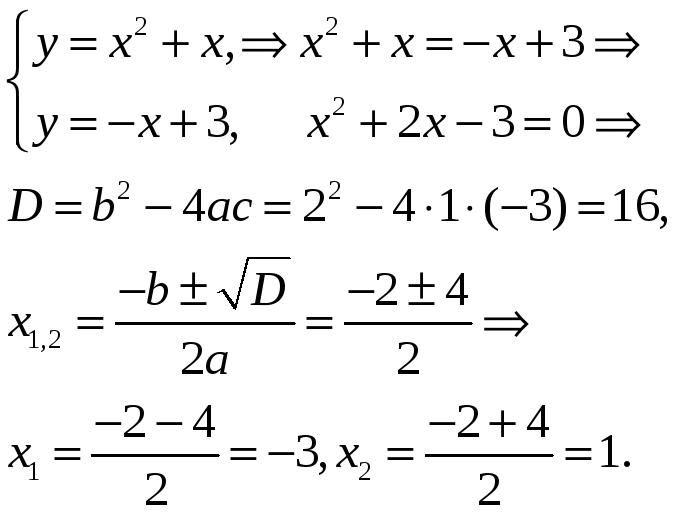
Тогда площадь
плоской области
![]() вычисляется
с помощью двойного интеграла, который
выражается через повторный:
вычисляется
с помощью двойного интеграла, который
выражается через повторный:
Рис.1.
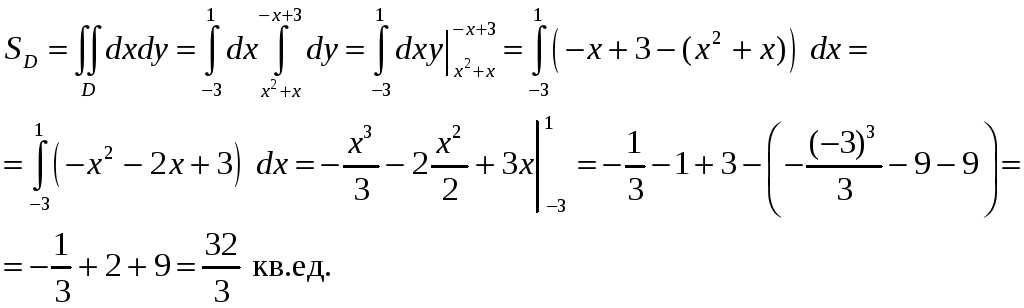
2. Вычислить
площадь фигуры
![]() ,
ограниченной линиями
,
ограниченной линиями![]() ,
,
![]() .
.
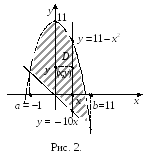
Решение.
Область интегрирования
![]() (рис.
2) ограничена сверху параболой
(рис.
2) ограничена сверху параболой
![]() ,
а снизу прямой
,
а снизу прямой
![]() .
Пределы интегрирования
.
Пределы интегрирования
![]() и
и
![]() определяются из
системы уравнений:
определяются из
системы уравнений:
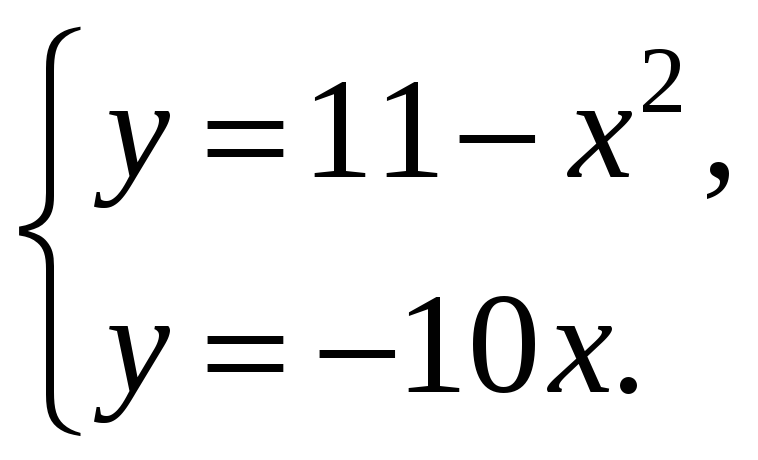
Отсюда получаем уравнение:
![]() или
или
![]() ,
которое имеет корни
,
которое имеет корни
![]() ,
,
![]() .
Таким образом, пределы интегриро-
.
Таким образом, пределы интегриро-
вания
![]() ,
,
![]() .
Тогда площадь
плоской области
.
Тогда площадь
плоской области
![]() вычисляется с по-
вычисляется с по-
мощью двойного интеграла, который выражается через повторный:
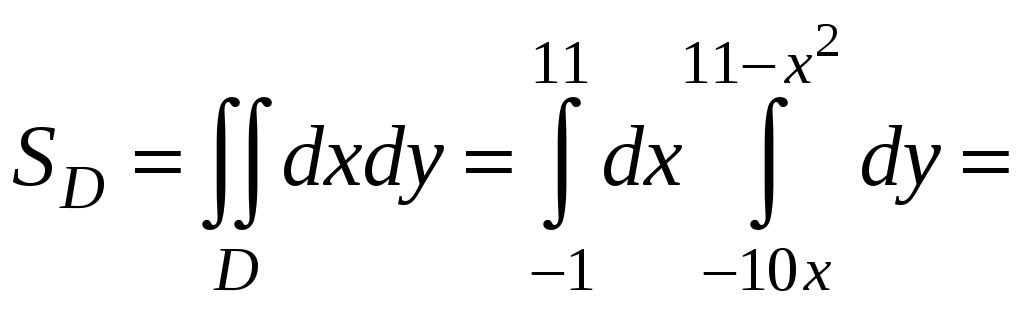
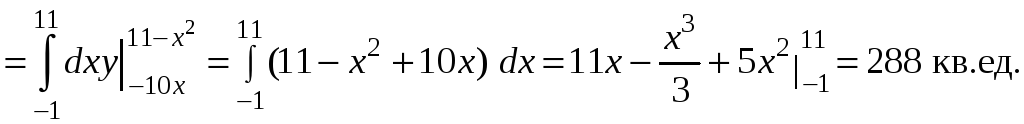
3.
Найти
работу силы
![]() при
перемещении вдоль линии
при
перемещении вдоль линии
![]() от точки
от точки
![]() к точке
к точке
![]() .
.
Решение.
Работа силы
![]() при перемещении вдоль линии
при перемещении вдоль линии
![]() от точки
от точки
![]() к точке
к точке
![]() находится
по формуле
находится
по формуле
![]()
Так
как на кривой
![]() ,
то
,
то
![]() причем
точке
причем
точке
![]() от-
от-
вечает значение
![]() ,
а точке
,
а точке
![]() отвечает
значение
отвечает
значение
![]() .
Тогда получим:
.
Тогда получим:
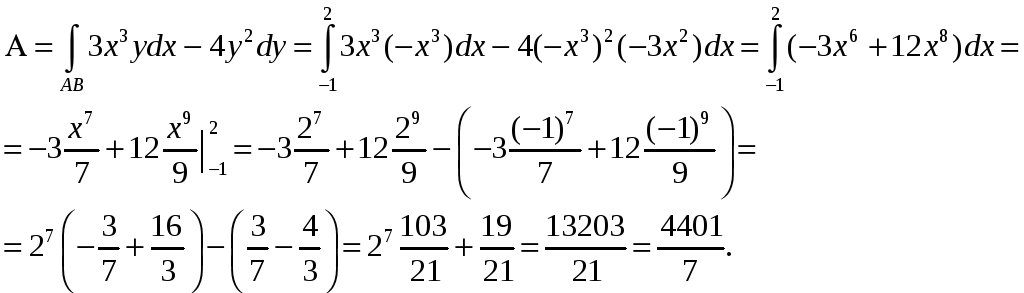
4.
Найти
работу силы
![]() при
перемещении вдоль отрезка прямой
при
перемещении вдоль отрезка прямой
![]() от точки
от точки
![]() к точке
к точке
![]() .
.
Решение.
Работа силы
![]() при перемещении вдоль отрезка прямой
при перемещении вдоль отрезка прямой
![]() от точки
от точки
![]() к точке
к точке
![]() находится по формуле
находится по формуле
![]()
Запишем каноническое
уравнение прямой
![]() ,
проходящей через точки
,
проходящей через точки
![]() и
и
![]() :
:
![]()
Отсюда следует
параметрическое уравнение прямой
![]() :
:
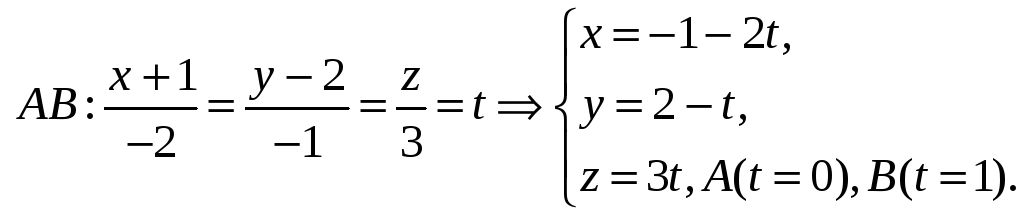
Тогда получим:
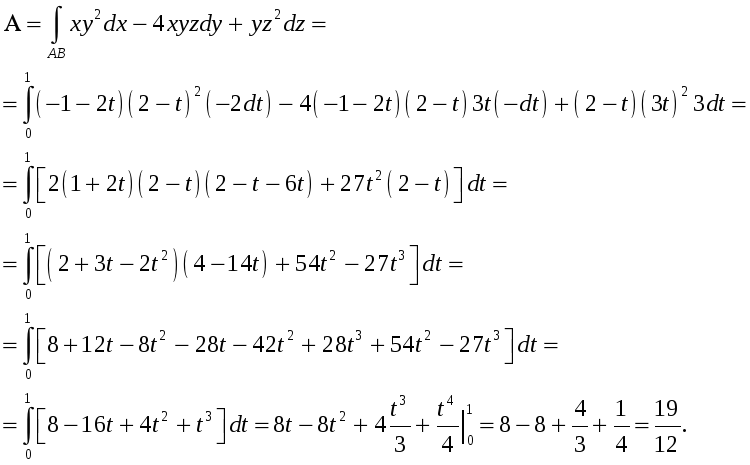
5.Найти
циркуляцию силы
![]() при перемещении вдоль контура
при перемещении вдоль контура
![]() (обход по контуру
(обход по контуру
![]() происходит против часовой стрелки).
происходит против часовой стрелки).
Решение.
Циркуляция
силы
![]() при
перемещении вдоль контура
при
перемещении вдоль контура
![]() находится по
формуле
находится по
формуле
![]()
Точки пересечения
линий
![]() и
и
![]() находим из системы уравнений:
находим из системы уравнений:

На
кривой
![]()
![]() меняется от
меняется от
![]() до
до
![]() ,
а на
кривой
,
а на
кривой
![]()
![]()
меняется от
![]() до
до
![]() .
Тогда получим:
.
Тогда получим: