6. Проверить потенциальность и соленоидальность векторного поля
.
Решение.
Векторное
поле
является
потенциальным, если ротор поля
равен
нулю:
.
Ротор поля
в базисе
дается формулой:
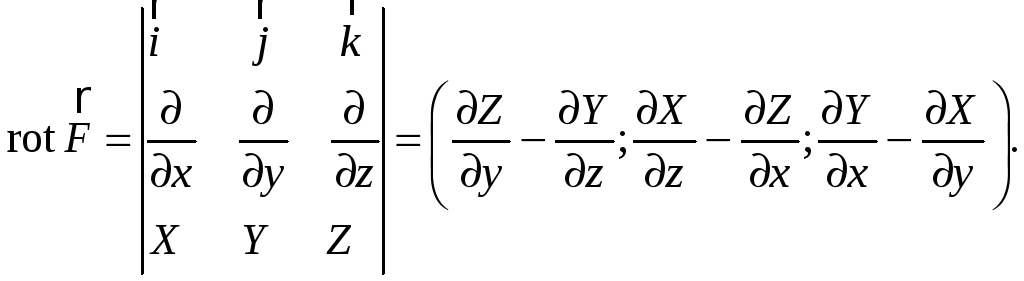
Находим:
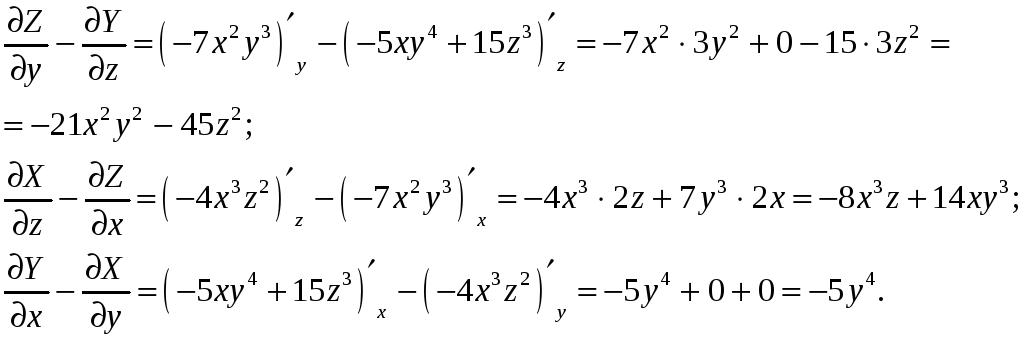
Следовательно,
,
а, значит, век-
торное поле
не
является потенциальным.
Векторное поле
является
соленоидальным, если дивергенция поля
равна
нулю:
.
Дивергенция поля
в базисе
дается
формулой:
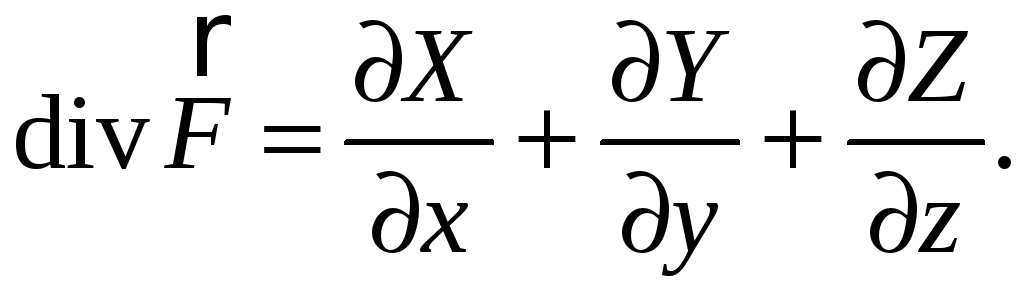
Находим:
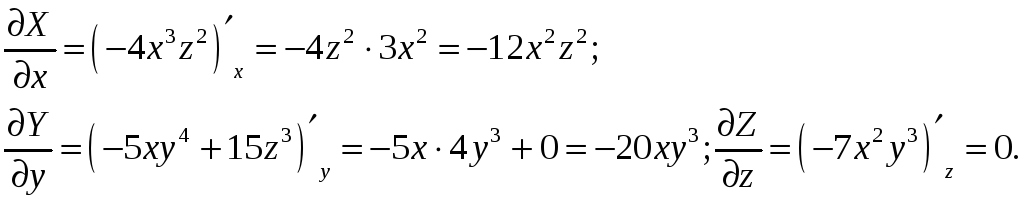
Следовательно,
,
а, значит, векторное поле
не
является соленоидальным.
7. Вычислить
Решение. Используя правила действия над комплексными числами, находим:
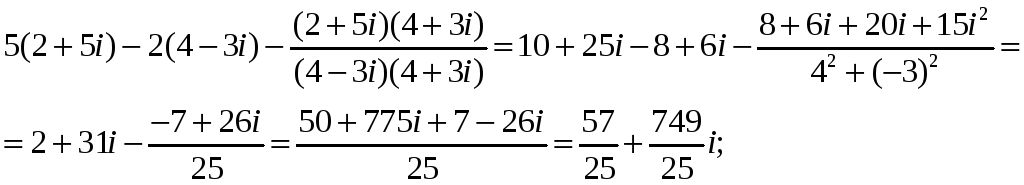
8.
Вычислить
интеграл
,
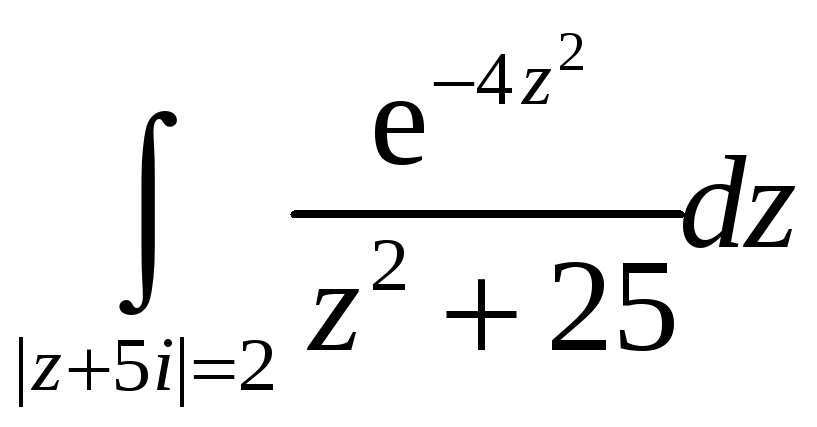используя основную теорему теории
вычетов. Построить контур интегрирования.
Решение.
Контуром интегрирования является
окружность
.
Сравни-
вая
общий вид уравнения окружности
с
,
находим:
.
В
комплексной плоскости переменной
строим
окружность
(рис. 3). Особыми точками подынтегральной функции являются нули знамена-
теля:
– полюсы
первого порядка подынтег-
ральной
функции.
Точка
попала
внутрь области,
ограниченной ок-
ружностью
.
Используя
основную теорему теории вычетов и
фор-
мулу
для вычета в полюсе
первого порядка,
,
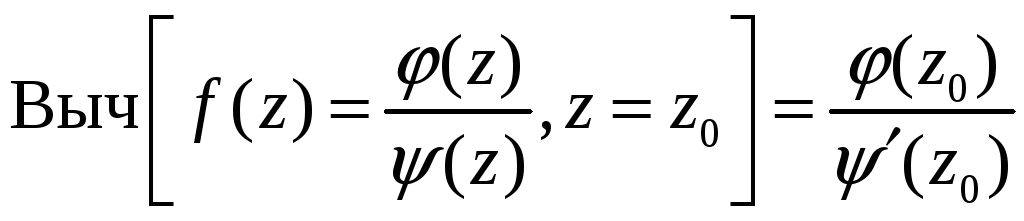находим:
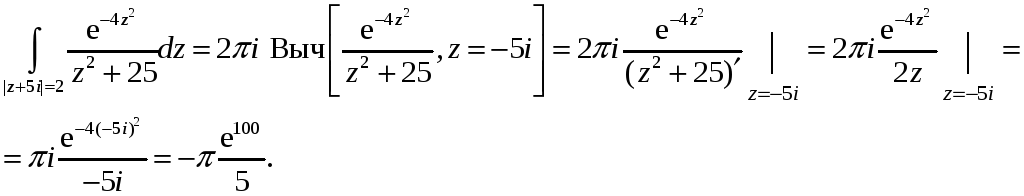
9.
Вычислить
интеграл
,
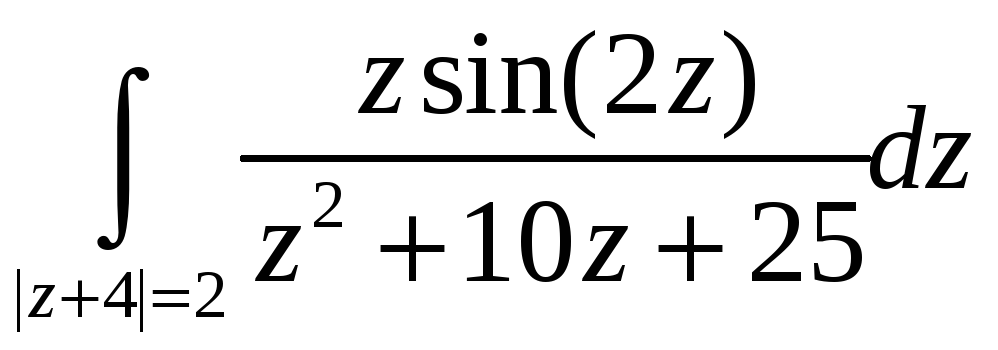используя основную теорему
теории вычетов. Построить контур интегрирования.
Решение.
Контуром интегрирования является
окружность
.
Сравнивая
общий вид уравнения окружности
с
,
находим:
.
В
комплексной плоскости переменной
строим
окружность
(рис. 4). Особыми точками подынтегральной функции являются нули знамена-
теля:
–
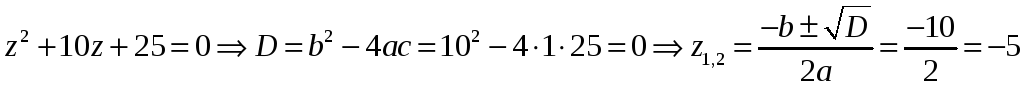полюсы второго
порядка подынтегральной
функции.
Точка
попала
внутрь области,
ограниченной окружностью
.
Используя
основную
теорему
теории вычетов и формулу для вычета в
полюсе
порядка,
,
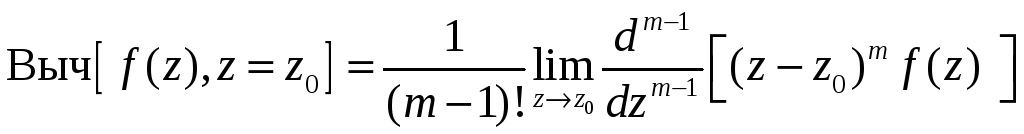находим:
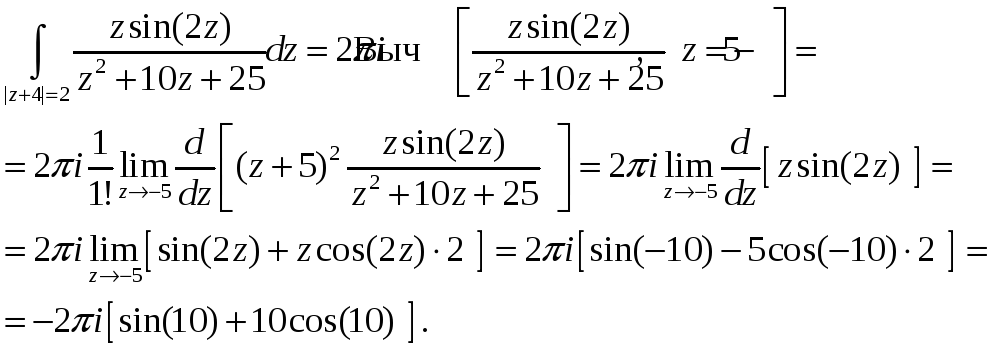
10. Вычислить производную аналитической функции в точке
Решение. Используя правила дифференцирования и таблицу производных, на-
ходим:
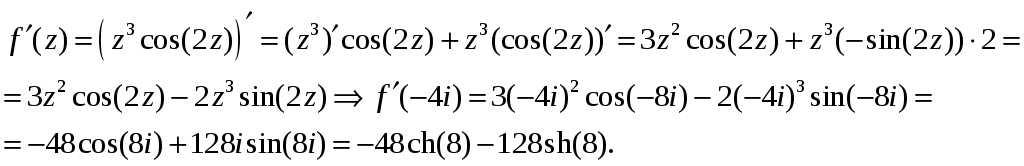
11. Решить задачу Коши операционным методом.
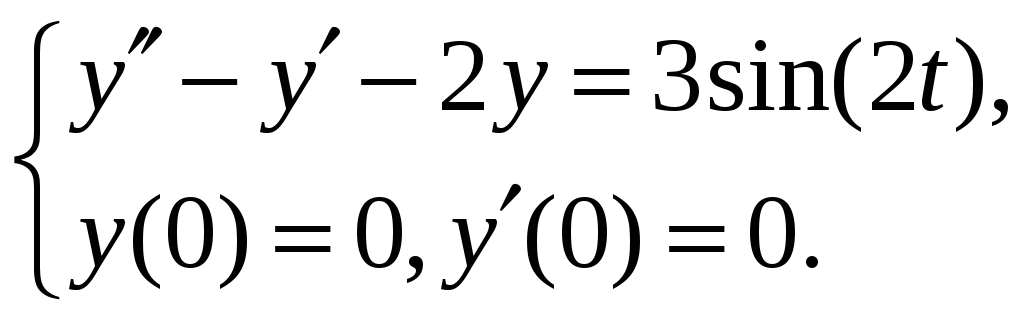
Решение.
Обозначим изображение Лапласа для
оригинала
через
Используя
формулу для изображения производной
и таблицу
изображений, находим:
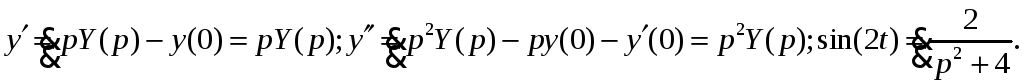
Тогда, подставляя найденные выражения в исходное дифференциальное
уравнение, получим:
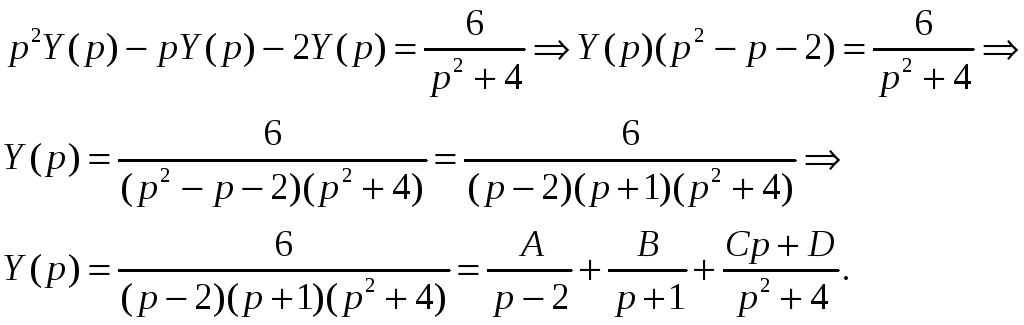
Коэффициенты
и
находим
методом вычеркивания, а коэффициенты
и
–
общим
методом:
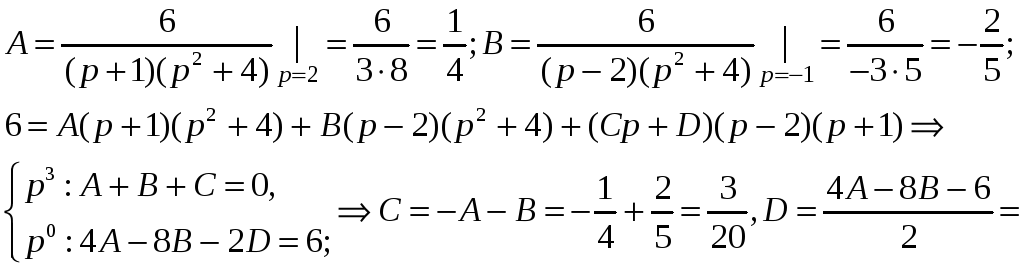
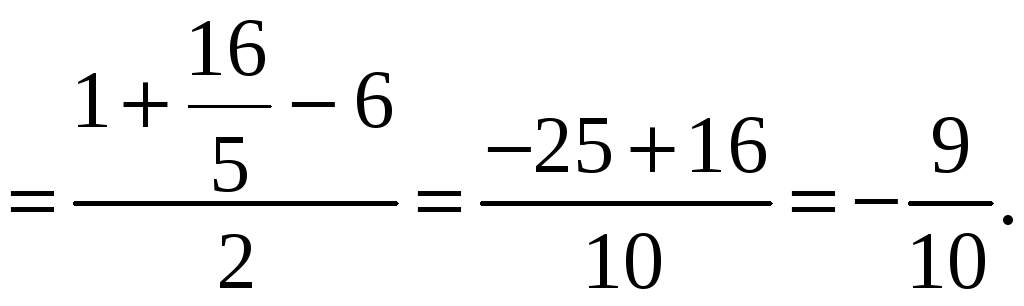
Следовательно,
для изображения
получим выражение:
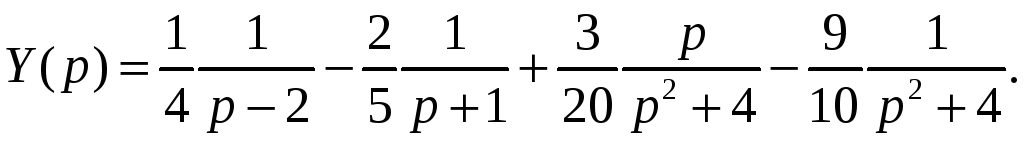
Отсюда, используя таблицу изображений, находим искомое решение:
12. Вычислить
и
Решение.
1) Запишем комплексное число
в показательной
форме:
.
Находим:
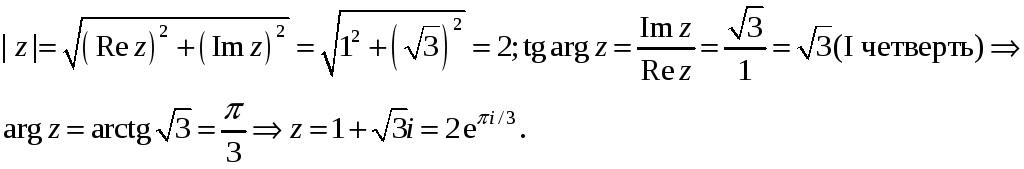
Тогда по правилу возведения комплексного числа в дробную степень получим:
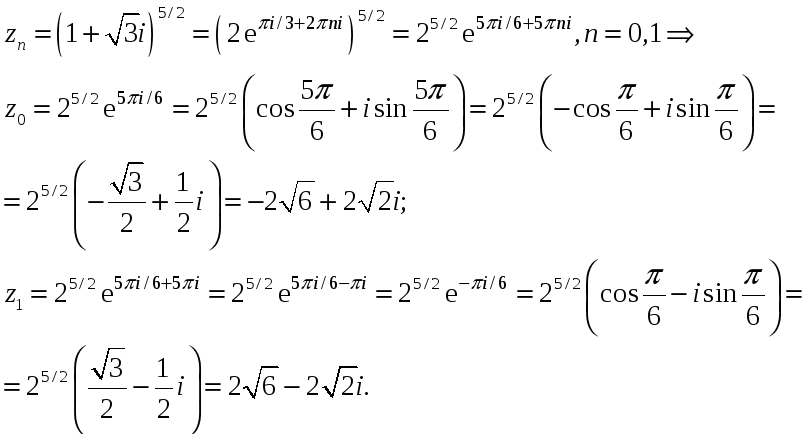
Здесь использовали
формулу Эйлера:
2) Запишем
комплексное число
в показательной
форме:
.
Находим:
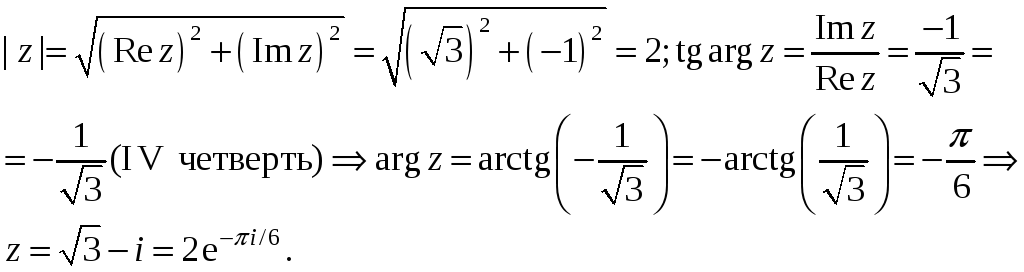
Тогда по правилу возведения комплексного числа в целую степень получим:
Здесь также
использовали формулу Эйлера:
