Лабы / Лабы (Бажанов) / Еще лабы / Лаба 3

Московский Государственный Институт Электронной Техники

(Технический Университет)

Лабораторная работа №3.

Обработка результатов измерений с многократными наблюдениями.

Выполнили:

Вольников М.

Врацкий О.

Пилюгин Д.

Спахиу А.

Проверили:

Бажанов Е. И.

Смирнова М. А.

Москва 2003

Цель работы: ознакомление с методикой определения результатов измерения с многократными наблюдениями.

Продолжительность работы: 4 часа.

Аппаратура: персональный компьютер.

^{Лабораторное задание.}

1. Ознакомиться с методикой выполнения работы на ЭВМ и ввести выборку наблюдений.

2. Определить оценку математического ожидания и оценку среднего квадратического отклонения для заданной выборки.

3. Проверить выборку на наличие промахов.

4. Проверить нормальность распределения выборки по критерию Х² Пирсона.

5. Определить и записать результаты измерения по МИ 1317-87.

Выборка:

14,06657	14,55216	14,72780	13,31202
13,05247	13,95179	13,05026	13,48217
13,32265	13,59183	13,16343	13,89888
13,69696	13,42802	12,27224	13,74549
12,45595	12,13914	12,30657	12,79489
12,55789	12,93274	12,63807	12,21130
15,98095	11,76651	11,31001	11,76291
11,87145

Расчёт математического ожидания, среднего квадратического отклонения:

1). M [x] = 13.05662

D [x] = 1.07314

[x] = 1.03593

 [M(x)] = 0.18913

3 [x] = 3.10779

Xср = 12.12121

Промахов не обнаружено.

Используя одну из формул: L= log 2 (n + 1); L=5*lg n; L=n; найдём, что число интервалов равно 6.

Разбиение произведём произвольно, в пределах 3.

1: 0.5000

2: 1.0000

3: 1.5000

Получим гистограмму следующего вида:

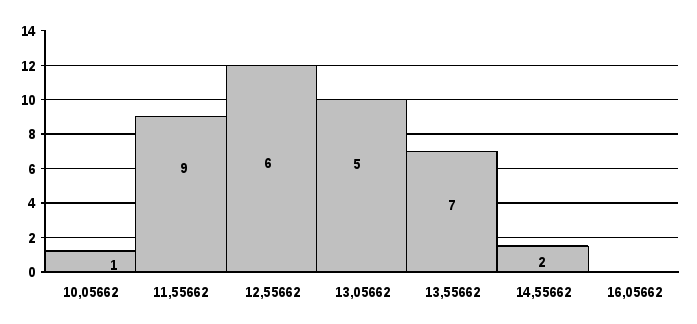
Проверим гипотезу, что результаты измерений принадлежат нормальному распределению с помощью критерия Х² Пирсона. Для этого подсчитаем теоретическое и практическое число попаданий результатов измерений в интервалы (N и N’). N’ – практическое - ищется непосредственно из гистограммы, а N – теоретическое – с помощью доверительной вероятности.

Nj = Pj*n, где Pj = ();  = x/[x]

a=0.31

P1 = 0.16

P2 = 0.4-0.16=0.24

P3 = 0.5-0.24-0.16=0.1

№	N’	P
1	4.8	0.16
2	7.2	0.24
3	3.0	0.1

X² пр = 2.43056

X² теор = 7.815

Сравнивая X²пр. и X²теор., получим: X²пр. < X²тр. Откуда следует: нет оснований отвергнуть теорию, что данное распределение принадлежит нормальному закону.

Вычислим доверительные границы погрешности:

A = t*[A], где t – коэффициент Стьюдента.

A = 2*0.18913 = 0.37826

R = 13.05662 0.37826

а <= ½ * 10^k-m (0.37826 <= ½ * 10^-1 )

m = 2; k = 2;

Количество значащих цифр:

13 = 1*10¹ + 3*10⁰ ; k = m = 2; n = m + 1 = 3

R = 13.06  0.38

Вывод:

В результате работы с мы не обнаружили промахов, вычислили на ЭВМ оценку математического ожидания и среднего квадратического отклонения. По гистограмме проверили нормальность распределения выборки по критерию Пирсона. В результате сравнения X²пр. и X²тр. выяснили, что при заданном уровне значимости нет оснований отвергнуть гипотезу, что данное распределение принадлежит нормальному закону. Также мы определили количество значащих цифр, заслуживающих доверие.