
Глава 2. Преобразование фурье. Свойства преобразования фурье.
2.1 Интегральная формула Фурье как предельный случай ряда.
Как следует из теории ряда Фурье, он применим при обращении с периодическими функциями и с функциями с ограниченным интервалом изменения независимых переменных ( поскольку этот интервал может быть расширен на всю ось путем периодического продолжения функции). Однако периодические функции сравнительно редки на практике. Эта ситуация требует создания более общего математического аппарата для обращения с непериодическими функциями, а именно интеграла Фурье и на его основе, преобразования Фурье.
Рассмотрим непериодическую функцию f(t) как предел периодической с периодом T=2l при l®¥.
Периодическая функция с периодом 2l может быть представлена в виде разложения в ряд Фурье ( воспользуемся комплексной его формой)
![]()
![]()
 (1)
(1)
где выражения для коэффициентов имеют вид:
![]() (2)
(2)
Введем следующее обозначение для частот:
![]() (3)
(3)
Запишем разложение
в ряд Фурье в виде одной формулы, подставив
в (1), выражение для коэффициентов
![]() (2) и для частоты (3) :
(2) и для частоты (3) :
 (4)
(4)
Спектр периодической функции с периодом 2l дискретный
![]() .
.
Обозначим
минимальное расстояние между точками
спектра, равное основной частоте
колебаний
![]() за
за
![]() ,
т.е.
,
т.е.

и введем это обозначение в (4):
 (5).
(5).
В таких обозначениях
ряд Фурье напоминает интегральную
сумму для функции
 .
.
Переходя к пределу
при T=2l®¥
к непериодической функции, получим,
что частотный интервал
 становится
бесконечно малым ( обозначим его за dw),
а спектр становится непрерывным. С
математической точки зрения это
соответствует замене суммирования по
дискретному набору интегрированием по
соответствующей переменной в бесконечных
пределах.
становится
бесконечно малым ( обозначим его за dw),
а спектр становится непрерывным. С
математической точки зрения это
соответствует замене суммирования по
дискретному набору интегрированием по
соответствующей переменной в бесконечных
пределах.
 (5)
(5)
Это выражение и есть интегральная формула Фурье.
2.2 Формулы преобразования Фурье.
Интеграл Фурье удобно представить в виде суперпозиции двух
формул:
![]() (6)
(6)
![]() (7)
(7)
Функция F(w), сопоставляемая по первой формуле функции f(t), называется ее преобразованием Фурье. В свою очередь, вторая формула, позволяющая найти исходную функцию по ее образу, называется обратным преобразованием Фурье. Обратим внимание на симметрию формул для прямого и обратного преобразования Фурье с точность до постоянного множителя 1/2p и знака в показателе экспоненты.
Символически прямое и обратное преобразование Фурье будем обозначать как f(t)~F(w).
Проводя аналогию с тригонометрическим рядом Фурье, можно прийти к выводу, что образ Фурье (6) является аналогом коэффициента Фурье (см.(2)), а обратное преобразование Фурье (7) является аналогом разложения функции в тригонометрический ряд Фурье (см.(1)).
Отметим, что
множитель
![]() вместо обратного преобразования можно
отнести к прямому преобразованию Фурье
или сделать симметричные множители
вместо обратного преобразования можно
отнести к прямому преобразованию Фурье
или сделать симметричные множители
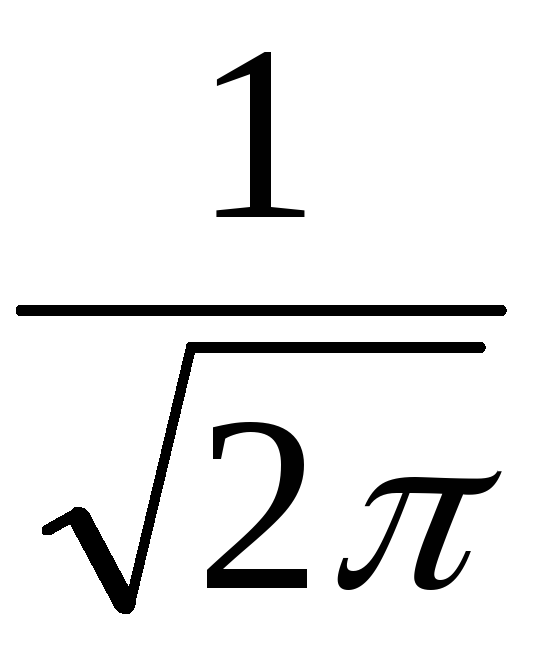 для прямого и
обратного преобразований . Главное,
чтобы оба преобразования вместе
составляли интегральную формулу Фурье
(5), т.е. произведение постоянных множителей
при прямом и обратном преобразовании
должно быть равно
для прямого и
обратного преобразований . Главное,
чтобы оба преобразования вместе
составляли интегральную формулу Фурье
(5), т.е. произведение постоянных множителей
при прямом и обратном преобразовании
должно быть равно
![]() ..
..
Отметим, что для прикладных целей более удобной оказывается не угловая частота w, а частота n, связанная с первой соотношением w=2pn. и измеряемая в герцах (Гц). В терминах этой частоты формулы преобразования Фурье будут иметь вид:
![]() (6б),
(6б),
![]() (7б).
(7б).
Сформулируем без доказательства достаточные условия существования преобразования Фурье.
1) f(t) - ограничена при tÎ(-¥,¥);
2) f(t) - абсолютно интегрируема на tÎ(-¥,¥);
3) Число точек разрыва, максимума и минимума функции f(t) конечно.
Другим достаточным условием является требование квадратичной интегрируемости функции на свей действительной оси, что физически соответствует требованию конечной мощности сигнала.
Таким образом, с помощью преобразования Фурье мы имеем два способа представления сигнала: временное f(t) и частотное F(w).
2.3 Свойства преобразования Фурье.
1. Линейность.
Если f(t)~F(w),g(t)~G(w),
то аf(t)+bg(t) ~aF(w)+bG(w).
Доказательство основано на линейных свойствах интегралов.
2. Четность.
2.1 Если f(t) действительная четная функция и f(t)~F(w), то F(w) также действительная четная функция.
Доказательство:
Используя определение (6), а также формулу Эйлера
![]() получим
получим
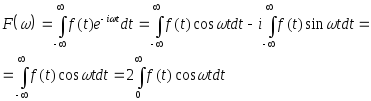
![]() -четная
функция.
-четная
функция.
2.2 Если f(t) -нечетная действительная функция,то F(w)- нечетная мнимая функция.

![]()
2.3 Если f(t) произвольная действительная функция, F(w) имеет четную действительную часть и нечетную мнимую часть.
Доказательство:

Cвойства четности 2 можно суммировать в формуле :
![]()
3. Подобие
Если f(t)~F(w),
то f(at) ~
![]() .
.

4. Смещение.
4.1 Если f(t)~F(w),
то f(t-a) ~![]() .
.
Т.е. запаздыванию во времени соответствует умножение на комплексную экспоненту в области частот.
![]()
4.2 Если f(t)~F(w),
то![]() ~
~![]() .
.
![]() Т.е.
смещение по частоте соответствует
умножению на комплексную экспоненту
во временной области.
Т.е.
смещение по частоте соответствует
умножению на комплексную экспоненту
во временной области.
5. Если f(t)~F(w),то
5.1 f’(t)~iwF(w),![]() ~
~![]()
если f(t) имеет n непрерывных производных .
Доказательство:
![]()
5.2
![]() ~
~![]() ,
,![]() ~
~![]() ,
,
если F(w) имеет n непрерывных производных.
Доказательство:
![]()
2.4 Важнейшие примеры нахождения преобразования Фурье.
1)
![]() ~
~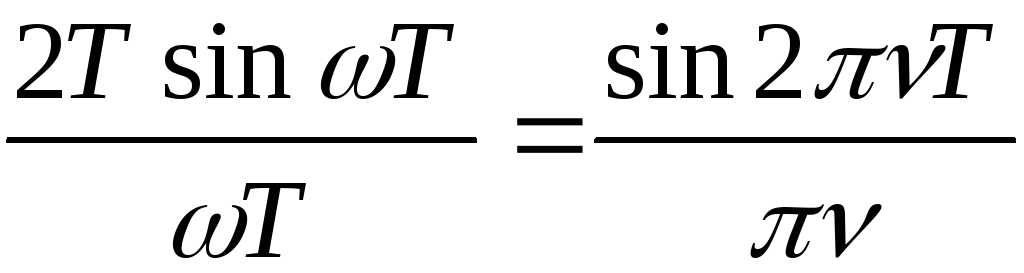
где
![]() -
прямоугольный импульс
-
прямоугольный импульс
![]()

2)
![]() ~
~

3)
![]() ~
~

При этом мы учли,
что
![]() - интеграл Пуассона.
- интеграл Пуассона.
Нахождение
последнего интеграла можно пояснить
следующим образом. Контур интегрирования
С есть прямая в комплексной плоскости
(t,w),
параллельная действительной оси
(w-постоянное
число). Интеграл от скалярной функции
по замкнутому контуру равен нулю.
Образуем замкнутый контур, состоящий
из прямой С и действительной оси t,
замыкающихся на бесконечности. Т.к. на
бесконечности подинтегральная функция
![]() стремится к нулю, то интегралы по
замыкающим кривым равны нулю. Значит
интеграл по прямой С равен интегралу,
взятому по действительной действительной
оси, проходимой в положительном
направлении.
стремится к нулю, то интегралы по
замыкающим кривым равны нулю. Значит
интеграл по прямой С равен интегралу,
взятому по действительной действительной
оси, проходимой в положительном
направлении.
