§ 7. Интегральная формула Коши. Интеграл Коши.

1. Интегральная формула Коши.

Пусть f(z) C^(). Выразимf(z₀) (z₀g) через значения f(z) на g.

(z)=f(z)/(z-z₀)  C^(/z₀).

Возьмем в области g произвольный такой замкнутый контур  : z₀  . (z)C^(g^*) (g^* - многосвязная область между g и ).

По теореме Коши для многосвязной области

: = z₀+e ^i, d = i e ^i d

В силу произвольности можем0.

f(z) C^()=> >0  : |f()-f(z₀)|<  как только |-z₀|< (!) =>



Т.о. или

- интеграл Коши

Замечания.

1. Формула верна как для g односвязной, так и g- многосвязной, только в последнем случае ⁺- полная граница области, проходимая в положительном направлении.

2. Интеграл Коши имеет смысл для  взаимного расположения точки z₀ и замкнутого контура  (не проходящего через z₀) в области аналитичности f(z)

2. Следствия интегральной формулы Коши.

Формула среднего значения.

Пусть z₀- некоторая внутренняя точка односвязной области g. Возьмем окружность C_R с центром в z₀ и радиусом R, C_R  g.

Тогда

C_R: = z₀+R e^i _; d = i Re^i d = i e^i ds (ds – дифференциал дуги)

Принцип максимума модуля. Если f(z) C^(), тогда или |f(z)|const или |f(z)| достигает своего максимального значения только на g. (Без доказательства)

§ 8. Интегралы, зависящие от параметра.

1. Дифференцирование интеграла, зависящего от параметра.

Из курса действительного анализа известно, что интеграл, зависящий от параметра, можно дифференцировать под знаком интеграла, если производная подынтегральной функции по параметру непрерывна.

2. Существование производных всех порядков в области аналитичности функции комплексной переменной.

Пусть f(z) C^(). Тогда значенияf(z) во всех внутренних точках области (zg) можно выразить через значения f(z) на g при помощи интеграла Коши .

Производная порядка n нашей подынтегральной функции по параметру z равна => она непрерывна везде внутриg => можно дифференцировать интеграл Коши произвольное число раз. Т.о. справедлива

Теорема 8.1. Пусть f(z) C^(), тогда внутриg существуют производные произвольного порядка и верна формула

.

Замечание. Существенное отличие комплексных функций от функций действительной переменной, для которых из существования первой производной, вообще говоря, не следует существование высших производных. Например, функция y(x)=x|x| непрерывна на всей числовой прямой; ее производная y'(x)=2|x| также непрерывна на всей числовой прямой, однако, y"(0) не существует!

3. Теоремы Морера и Лиувилля.

Теорема Морера. Если f(z)C(g), g-односвязная и для  замкнутого g: , то f(z) C^(g).

Доказательство. При условиях теоремы   C^(g) (Теорема 6.1.), где z₀ и z- произвольные точки g, а интеграл берется по  пути внутри g, соединяющему эти точки. При этом F'(z)=f(z). Но производная аналитической функции сама является аналитической функцией (Теорема 8.1), в частности  F"(z)= f '(z) C(g).

Теорема Лиувилля. Если f(z)- аналитическая на всей комплексной области и  M: |f(z)|M, f(z)  const.

Доказательство. Выразим значение f '(z) в произвольной точке z через значения функции на окружности радиуса R с центром в точке z

.

На C_R: | -z|=R. По условию теоремы  M: |f()|M не зависимо от R=>

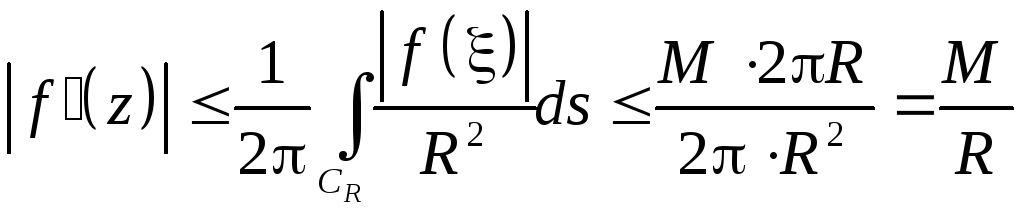
Устремив R, получим |f '(z)|=0  f(z)=const для  z.

Замечание. Отсюда, в частности следует, что  z: |sin(z)|>1.