
- •1.2. Наибольший общий делитель н наименьшее общее кратное
- •1.3. Вычисление наибольшего общего делителя
- •1.3.1. Алгоритм Евклида
- •1.4. Простые числа
- •1.4.2. Распределение простых чисел
- •Глава 2 сравнения с одним неизвестным
- •2.1. Отношение сравнимости
- •2.2. Решение сравнений
- •2.2.1 Сравнения первой степени
- •2.2.2. Китайская теорема об остатках
- •2.2.3. Сравнения произвольной степени по простому модулю
- •2.3. Сравнения второй степени
- •2.3.1. Символы Лежандра и Якоби
- •Решение сравнений для случаев простого модуля.
- •Случаи составного модуля
Решение сравнений для случаев простого модуля.
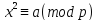 ,
где
число р
не делится на 2 и простое и целое число
a
не
делится на р.
,
где
число р
не делится на 2 и простое и целое число
a
не
делится на р.
Для
того чтобы сравнение было разрешимо
необходимо и достаточно, чтобы символ
Лежандра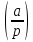 был равен 1, тогда сравнение имеет ровно
2 решения.
был равен 1, тогда сравнение имеет ровно
2 решения.
Пуст
p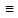 3
(mod
4), то есть p=4m+
3, где m
3
(mod
4), то есть p=4m+
3, где m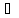 Z.
Разрешимость сравнения означает, что
Z.
Разрешимость сравнения означает, что
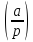 = 1.
По свойству 3 символа Лежандра 1 =
= 1.
По свойству 3 символа Лежандра 1 =
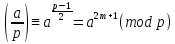 .
.
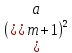 =
=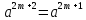 ∙a
∙a
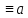 (modр).
Таким
образом, решение имеет вид
(modр).
Таким
образом, решение имеет вид
 (mod
р).
(mod
р).
Пусть
р
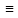 5 (mod
8), то есть р
= 8m
+ 5, где
m
5 (mod
8), то есть р
= 8m
+ 5, где
m Z.
Разрешимость сравнения означает, что
Z.
Разрешимость сравнения означает, что
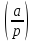 = 1.
По свойству 3 символа Лежандра
= 1.
По свойству 3 символа Лежандра
1
=
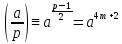 (mod
p)=
(mod
p)=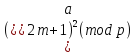 .Отсюда
.Отсюда
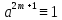 (mod
p) или
(mod
p) или
 (mod
p). В
первом случае, умножая обе части сравнения
на a,
получаем
(mod
p). В
первом случае, умножая обе части сравнения
на a,
получаем
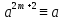 (mod
p)
(mod
р), то есть решение имеет вид
(mod
p)
(mod
р), то есть решение имеет вид
 (mod
р).
(mod
р).
При
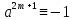 (mod
p)
ситуация немного сложнее. Заметим, что
при р
(mod
p)
ситуация немного сложнее. Заметим, что
при р
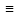 5 (mod
8) число 2 является квадратичным невычетом
по модулю р.
Действительно,
5 (mod
8) число 2 является квадратичным невычетом
по модулю р.
Действительно,
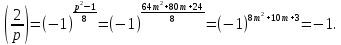 |.
По свойству 3 символа Лежандра
|.
По свойству 3 символа Лежандра
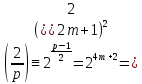 (mod
р). Таким образом,
(mod
р). Таким образом,
 (mod
р). Тогда
(mod
р). Тогда
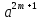 ∙
∙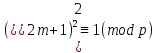
Умножая
обе части этого сравнения на a,
получаем решение сравнения
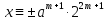 (mod
р).
(mod
р).
Здесь вместо числа 2 можно брать любой другой квадратичный невычет по модулю р.
Пусть
p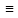 1
(mod
8). Представим р
в виде р
= 2k∙h
+ 1, где k≥З,
число
h
нечетное. Разрешимость сравнения
означает, что
1
(mod
8). Представим р
в виде р
= 2k∙h
+ 1, где k≥З,
число
h
нечетное. Разрешимость сравнения
означает, что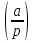 = 1.
= 1.
По
свойству 3 символа Лежандра 1 =
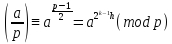 .
Отсюда
.
Отсюда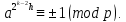 Пусть
N
—
произвольный квадратичный невычет по
модулю p,
то
есть -1 =
Пусть
N
—
произвольный квадратичный невычет по
модулю p,
то
есть -1 =
 (mod
р). Тогда при некотором целом
S2≥0
получим
(mod
р). Тогда при некотором целом
S2≥0
получим
 (mod
р), откуда
(mod
р), откуда
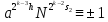 (mod
р). Далее, при
некотором целом S3≥0
получим
(mod
р). Далее, при
некотором целом S3≥0
получим
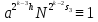 (mod
р), откуда
(mod
р), откуда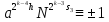 (mod
р) и т.д. Получив сравнение
(mod
р) и т.д. Получив сравнение
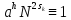 (mod
р)
для некоторого целого
(mod
р)
для некоторого целого
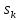 ≥ 0 и умножив обе его части наа,
получаем решение
≥ 0 и умножив обе его части наа,
получаем решение
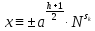 (mod
р).
(mod
р).
Алгоритм 2.2. Решение сравнения второй степени по модулю простого числа [4].
Вход:
Простое число р≠2;
такие целые числа a,
N,
что

Выход:
Решение
сравнения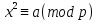 .
.
Представить число р в виде р = 2k • h + 1, где число h нечетное.
Положить a1←
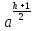 (mod
p), a2←
(mod
p), a2←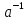 (mod
p),
(mod
p),
 (mod
p),
(mod
p),
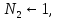 j←0.
j←0.Для i = 0,1, ...,k-2 выполнять следующие действия.
Положить b←a1N2 (mod p).
Вычислить c←a2b2(mod p).
Вычислить абсолютно наименьший вычет d←
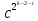 (mod
p).
При
d=1
положить ji←0,
при d=-1
положить ji←1.
(mod
p).
При
d=1
положить ji←0,
при d=-1
положить ji←1.Положить N2 ← N2
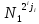 (mod
р).
(mod
р).
4. Результат:
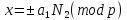 Сложность
этого алгоритма равнаO(log4p).
Сложность
этого алгоритма равнаO(log4p).
Случаи составного модуля
Теорема
2.11.
Пусть число р
простое, p≠2,
целое число a
не делится на
р
и
n N,
n≥
1. Для того чтобы сравнение
N,
n≥
1. Для того чтобы сравнение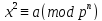 было
разрешимо, необходимо и достаточно,
чтобы было разрешимо сравнение
было
разрешимо, необходимо и достаточно,
чтобы было разрешимо сравнение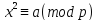
Определение
2.8.
Порядком
числа
a,
1
≤ a
<m,
НОД(а,
m)=
1,
по модулю m
называется наименьшее натуральное
число d,
для которого
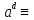 1 (mod
m).
1 (mod
m).
Определение 2.9. Число a, 1 ≤ a <m, порядка φ(m) по модулю m называется первообразным корнем по модулю m.
Свойство
2.12.
Для числа а,
имеющего
порядок
d
по
модулю m,
сравнение
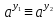 (mod
m)
выполняется тогда и только тогда, когда
(mod
m)
выполняется тогда и только тогда, когда
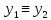 (mod
d).
(mod
d).
Свойство.
Если число а
имеет
порядок
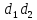 по
модулют,
то
число
по
модулют,
то
число
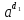 имеет
порядок
имеет
порядок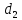 по
модулю
m.
по
модулю
m.
Свойство
2.14.
Если числа
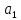 ,
,
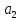 имеют
по модулю
m
порядки
имеют
по модулю
m
порядки
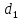 ,
, соответственно,
причем НОД(
соответственно,
причем НОД(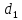 ,
,
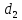 )=1,
то число
)=1,
то число
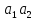 имеет по модулюm
порядок
имеет по модулюm
порядок
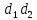 .
.
Теорема 2.15. Для любого простого р≠ 2 существует первообразный корень по модулю р.
Теорема
2.16.
Для
любого простого р≠
2
существует
первообразный корень по модулю
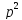 .
.
Теорема 2.17. Если сравнение разрешимо, то оно имеет ровно два решения.
Следствие.
Число квадратичных вычетов по модулю
 гдер—
простое число, р
≠ 2, равно числу квадратичных невычетов
по модулю
гдер—
простое число, р
≠ 2, равно числу квадратичных невычетов
по модулю
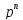 .
.
