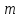2.3.1. Символы Лежандра и Якоби

Определение 2.6. Рассмотрим сравнение х² a (mod m), (2.8) где число р простое, р ≠ 2, а не делится на р. Определим для таких а и р символ Лежандра

Таким образом, если , то a – квадратичный вычет по модулю p, если , тоa – квадратичный невычет по модулю p.

Замечание. Понятие символа Лежандра можно обобщить и на случай, когда a делится на р. Тогда полагают = 0.

Символ Лежандра обладает следующими свойствами для любых целых чисел а, b, не делящихся на простое число р ≠ 2.

1. для любогоkZ.

Доказательство. Равенство выполняется, поскольку a + kpa (mod p) для любого kZ. Таким образом, если a b (mod р), то

2. =

Доказательство. Так как НОД(b,р)=1, существует b^-1(mod p). Тогда сравнения х²ab² (mod р) и (b^-1 x)² a (mod р) разрешимы или не разрешимы одновременно.

3. (modp). В частности, =1 для любого простого p2, = 1 при p 1(mod 4) и = -1 прир3 (mod4).

Доказательство. Согласно малой теореме Ферма, а ^p-1 1 (mod p). Тогда а^p-1-1=( - 1)(+ l)0(mod р). Оба сомножителя в этом сравнении на р делиться не могут, так как иначе их разность, рав­ная 2, делилась бы на р. Таким образом, для каждого а, 1≤а<р, выпол­няется ровно одно из сравнений

, (2.9)

, (2.10)

Если а — квадратичный вычет по модулю р, то существует такое число с, что a с² (mod р). Возводя обе части этого сравнения в степень и воспользовавшись малой теоремой Ферма, получаем

то есть любой квадратичный вычет удовлетворяет сравнению (2.9). При этом, согласно теореме 2.8, сравнение не может иметь болеерешений. Следовательно, квадратичные невычеты удовлетворяют сравнению (2.10).

4. =

Доказательство. Дважды применяя свойство 3, получаем =(mod p).

Таким образом, разность -делится наp. Число p простое, а символ Лежандра принимает значения -1, 1, значит, делимость возможна лишь в том случае, когда -.

5. Лемма 2.9 (Гаусс). , где µ — число отрицатель­ных вычетов среди абсолютно наименьших вычетов чисел a, 2*a,…,

Доказательство. Пусть ±m_k — абсолютно наименьший вычет, соответствуюший числу ka, где m_k > 0. При изменении значения k от 1 до число µ — это число знаков «-» при m_k. Покажем, что m_k ≠ m_l если k≠l и 1≤k, l≤ Действительно, равенство m_k =m_l означает, что ka± la (mod p). Поскольку а не делится на р, можем разделить обе час­ти сравнения на a. Получим k( mod p), то есть k±l. Но это невозможно, поскольку |k±l| ≤ k+l ≤р-1 и, кроме того, k≠l . Зна­чит, все элементы множества { m₁, m₂,... } различны, и это множество совпадает с множеством { 1, 2,... }.Перемножая сравнения a±m₁ (mod p), 2a±m₂(mod p), .... a± (mod p), получаем

((p -1)/2)! • a² ((p -1)/2)! (mod p).

Поскольку число ((р-1)/2)! не делится на р, поделим на него обе части сравнения: . Применяя свойство 3 и учитывая, что символ Лежандра принимает только значения 1 и -1, получаем тре­буемое равенство. □

5. , то есть , при p±1(mod 8); , приp±3(mod 8).

Доказательство. Рассмотрим систему вычетов 2 *1, 2*2, .... 2 *модулюр. В обозначениях леммы Гаусса число µ равно числу тех элементов этой системы, которые больше, чем . Зададим це­лое числоm двойным неравенством: . Тогда µ=

Дальнейшие выкладки для всех возможных значений р запишем в таблицу:

p				µ
8k+1	4k	4k-2<2m≤4k	2k	2k	1
8k+7	4k+3	4k+1<2m≤4k+3	2k+1	2k+2	1
8k+3	4k+1	4k-1<2m≤4k+1	2k	2k+1	-1
8k+5	4k+2	4k<2m≤4k+2	2k+1	2k+1	-1

7. При изменении а от 1 дор - 1 символ Лежандра принимает зна­чения 1 и -1 одинаково часто.

Доказательство. Квадратичными вычетами по модулю р являются те и только те числа, которые сравнимы с 1², 2², … ((р-1)/2)². Все эти числа различны. Действительно, из a²b² (mod р) для 0 < а < b ≤следует, что а b (mod р) или а -b р - b (mod р). Остальные чисел являются квадратичными невычетами по модулюр. □

Теорема 2.10 (квадратичный закон взаимности Га­усса). Пусть р и q — различные простые числа, р ≠ 2, q ≠2. Тогда

=

Другими словами, 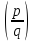= -, еслиpq, и =в противном случае.

Обобщением понятия символа Лежандра является символ Якоби.

Определение 2.7. Пусть m,nZ, где n= р₁р₂...р_r и числа р_i ≠ 2 простые (не обязательно различные). Символ Якоби опреде­ляется равенством

=

Если число n — простое, то символ Якоби является символом Ле­жандра.

Символ Якоби обладает следующими свойствами.

1. принимает значения 0, 1 или -1, причем 0 тогда и

только тогда, когда НОД(а, n) ≠ 1. Полагают = 1.

2. для всех a,kZ.

3.для всеха, b Z, НОД(b, n) = 1.

4. =для всех а, b Z.

5. = l; = . Следовательно,= 1 приn1(mod4);= -1 при n1(mod4);

Доказательство. Равенство 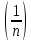= l выполняется по определе­нию символа Якоби. Для доказательства второго равенства отметим, что для нечетных чисел р₁ = 2k₁ + 1, p₂=2k₂+1 выполняется сравнение

Действительно, =2k₁∙k₂= 4 k₁ k₂ 0 (mod 4), поэто­му =++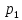-2 (mod 4). По­делив крайние части и модуль этого сравнения на 2, получим требуемое соотношение. По индукции получаем

Тогда ===.

6. .Следовательно, 1 при n ±1 (mod 8); -1 при n ±3 (mod 8).

Доказательство. Отметим, что для нечетных чисел р₁, р₂ вы­полняется сравнение

Действительно, каждое из чисел и делится на 4, то есть()( )0 (mod 16), поэтому (mod 16). Поделив обе части сравнения и модуль на 8, получим требуе­мое соотношение. По индукции получаем

Тогда ===.

7. Для нечетных целых чисел m, n справедливо равенство

=

Доказательство. Если m = ,n = то с учетом свойства 4, определения символа Якоби и квадратичного закона взаимности имеем =. Сумму в показателе степени достаточно вычислить по модулю 2. Получаем

то есть числа и имеют одинаковую четность, и

Из свойств символа Якоби следует, что если n — нечетное целое число и а=2^k , где число нечетное, то

Отсюда получаем алгоритм вычисления символа Якоби .

Алгоритм 2.1. Вычисление символа Якоби.

Вход. Нечетное целое число n ≥3. целое число а, 0≤ а < n.

Выход. Символ Якоби

1. Положить g←1.

2. При а = 0 результат: 0.

3. При а = 1 результат: g.

4. Представить а в виде а = 2^k|, где число нечетное.

5. При четном k положить s← -1. При нечетном k положить s←1, если n 1 (mod 8); положить s← -1, если n 3 (mod 8).

6. При результат:g ∙ s.

7. Если n 3 (mod 4) и 3 (mod 4), то s ← -s

8. Положить а ←n (mod ), n←g ←g ∙ s и вернуться на шаг 2.

Сложность алгоритма равна O(log²n).