Определение 1. Множество натуральных чисел N определяется с использованием аксиом Пеана

1. 

2. - последующее для

3. 

4. 

5. Если некоторое подмножество является таким, что

Сложение:

должны выполняться законы:

1. a+1=

2. (a+b)+c=a+(b+c) – ассоциативность

3. a+b=b+a – коммутативность

4. Если a+b=a+c, то b=c

Умножение:

можно единственным образом сопоставить им произведение

a*b=(….(a+a)+…+a) - b раз

1. a*1=a

2. a*=ab+a

3. (ab)c=a(bc)

4. ab=ba

5. (a+b)c=ac+bc

6. Если ab=ac, то b=с

выполняется 1 из 3 транзитивных отношений: a>b, a<b, a=b

Определение 2. Множество Z целых чисел определяется как объединение множеств N, отрицательных N и нуля

Определение 3. Пусть над некоторым множеством R произвольной природы определены операции сложения и умножения. Множество R называется кольцом, если выполняются следующие условия:

1. a+b=b+a

2. 

3. 

4. 

5. 

Определение 4. Если в кольце R умножение коммутативно (ab=ba), то кольцо R называется коммутативным

Определение 5. Если в кольце R умножение ассоциативно( (ab)c=a(bc)), то кольцо R называется ассоциативным

Определение 6. Если в кольце R существует единичный элемент e, такой что ae=ea=a, то R называется кольцом с единицей

Определение 7. Если в ассоциативном, коммутативном кольце R с единицей

то кольцо называется полем

Говорят, что целое число a делится нацело на целое число b>0, если существует целое число c, такое что a=bc. Число а называют кратным числа b, число b — делителем числа а, число с — частным от деления а на b.

Свойства деления:

1. Нуль делится на любое целое число

2. Если a₁ делится на b, a₂ делится на b, то а₁ ± а₁ делится на b

3. Если a₁ ± a₂ делится на b и а₁ делится на и, то a₂ делится на b

4. Любое целое число делится на 1

5. Если a делится на b и b делится на c, то a делится на c

6. Если 1 делится на a, то a=±1

Определение 1.5. Пусть числа а и b целые и b≠ 0. Разделить а на b с остатком — значит представить а в виде a=qb + r, где q,rZ и 0<r<|b|. Число q называется неполным частным, число r — остатком от деления а на b.

Теорема 1.1 (о делении с остатком). Для любых a,b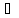Z, b≠0, существует единственная пара таких чисел q,r Z, что a = qb + r; 0<r<|b|.

Доказательство. Сначала докажем теорему для случая а ≥0, b > О,

N = {nN }.

Множество N «непусто» поскольку 0 Кроме того, для любого п Nвыполняется неравенство п≤ nb, а значит, п ≤ а. Таким образом, вес элементы множества N ограничены сверху числом а, и в множестве N существует наибольший элемент q. Но тогда qb ≤ а < (q + 1)b. Обозна­чим r = a-qb,тогда получаем требуемое неравенство для r:

0≤r = a-qb<(q + 1)b-qb = b.

Теперь найдем требуемую пару чисел q и r для а < 0, b >0. Со­гласно предыдущему случаю, для -а > 0 и b существуют целые числа 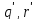такие, что -а = b + . При = 0 полагаемq = -,r = 0. При > 0 полагаем

q= -(q' + l), r=b-

При b < 0 нужно разделить с остатком а на |b| согласно одному из рассмотренных случаев: а = q'|b| + r, а затем положить q = -

Единственность докажем от противного. Пусть существуют две такие пары целых чисел q₁,r₁,q₂,r₂ что

a=q₁b + r₁ =q₂b + r₂,

где 0≤r₁ ,r₂ < |b|. Тогда

(q₁-q₂)b=-(r₁-r₂)

откуда следует

|q₁-q₂||b|=|r₁-r₂|<|b| , 0≤|q₁-q₂|<1

а так как числа q₁ и q₂ целые, то |q₁-q₂|=0 , q₁=q₂, r₂=r₁.

1.2. Наибольший общий делитель н наименьшее общее кратное

Определение 1.6. Целое число d≠0 называется наибольший общим делителем целых чисел а₁, а₂, ...,а_к (обозначается d = НОД(а₁, а₂, .... a_k)), если выполняются следующие условия:

1. каждое из чисел а₁, a₂,.... a_k делится на d;

2. если d₁≠ 0 — другой общий делитель чисел а₁, а₂,...a_k, то d делится на d₁

Ненулевые целые числа а и b называются ассоциированными (обо­значается а ~ b), если а делится на b и b делится на а.

Теорема 1.2 (об ассоциированных числах). Числа а и b ассоциированы тогда и только тогда, когда а = ±b.

Доказательство. Пусть а делится на b, тогда существует такое це­лое число с, что а=bс. Поскольку |c| ≥ 1, получаем |a|= |b|*|c|≥|b|*1=|b|, то есть |a|≥|b|

В то же время b делится на а. Проводя аналогичные выкладки, по­лучаем |b|≥ |а|. Таким образом, |a| = |b|, то есть а = ±b.

Теорема 1.3 (о единственности наибольшего обще­го делителя). Пусть числа a₁, а₂, .... a_k целые и d₁—их наибольший общий делитель. Целое число d₂ является наибольшим общим делителем чисел а₁, а₂,.... а_k тогда и только тогда, когда d₂ ~d₁.

Доказательство. Число d₁ — наибольший общий делитель чисел a₁, a₂… a_k, а d₂ — общий делитель этих чисел. Значит, по определению наибольшего общего делителя, d₁ делится на d₂. Точно так же, если рас­сматривать d₂ как наибольший общий делитель чисел a₁, a₂,…a_k, a d₁— как общий делитель этих чисел, то d₂ делится на d₁. Таким образом, d₁ ~ d₂. Необходимость доказана.

Теперь докажем достаточность. Пусть d₂ ~ d₁. Тогда, по определению наибольшего общего делителя, каждое из чисел а₁, а₂,... a_k делится на d_1. Кроме того, числа d₁ и d₂ ассоциированы, поэтому d₁ делится на d₂. Значит, каждое из чисел а_1, a₂, .... a_k делится на d₂. Таким образом, d₂ — общий делитель чисел а₁, а₂, ...,a_k. Покажем теперь, что он наибольший.

Пусть δ — некоторый общий делитель чисел а₁, а₂,...a_k. По условию d₁ = НОД(a₁, а₂ …a_k) , тогда d₁ делится на δ. А раз d₂ ~ d₁, то d₂ делится на d₁, значит d₂ делится на δ и d₂ = НОД(a₁, а₂, …a_k).

Учитывая теоремы 1.2, 1.3, далее для определенности наиболь­ший общий делитель целых чисел будем считать положительным чис­лом.

Теорема 1.4 (о существовании и линейном пред­ставлении наибольшего общего делителя). Для любых це­лых чисел а₁, а₂, .... a_k существует наибольший общий делитель d, и его можно представить в виде линейной комбинации этих чисел: d= c₁a₁ + c₂a₂ + ... + c_ka_k, где с_i Z.

Доказательство [I]. Пусть A = { c₁a₁ + c₂a₂ + ... + c_ka_k | с_i Z} — множество всевозможных целочисленных линейных комбинаций чисел а₁, а₂,.... а_k. Будем считать, что не вес числа а₁, а₂,… а_k нулевые, тогда в множестве А существует наименьший положительный элемент. Обо­значим его d. Покажем, что множество А совпадает с множеством всех целых чисел, кратных d. Поскольку число d может быть представлено в виде линейной комбинации чисел а₁, а₂, ....a_k то и любое число вида x_id где xZ, может быть представлено в виде линейной комбинации этих чисел.

Обратно, любая линейная комбинация чисел а₁, а₂ …а_k делится на d. Действительно, применим к числу d и произвольному элементу у 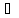А теорему о делении с остатком: существуют такие целые числа q и r, что y=qd+ r, причем 0≤r<d. Число r=y — qd является элементом множества А. поскольку у 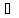Аи d А. Но d — наименьший неотрица­тельный элемент множества А, значит, r = 0 и y=qd. Таким образом, A={x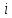d|x_i}.

Осталось доказать, что d — это наибольший общий делитель чисел a₁, а₂…a_k. Каждое из этих чисел имеет вид x_id, где хZ (достаточно рассмотреть линейную комбинацию вида 0*a1 + 0*a₂ + … + 0 * a_i-1 + 1*а_i, + 0 *a_i+1 +… + 0 * а_k). Таким образом, d — общий делитель чисел а₁, а₂,.... a_k.

Пусть с — любой другой делитель этих чисел. Тогда по свойству 2 делимости с делит каждую линейную комбинацию вида с₁а₁ + c₂a₂ + ... + c_ka_k, в том числе и ту, которая равна d. □

Определение 1.7. Целые числа а₁, a₂, .... а_к называются вза­имно простыми в совокупности, если НОД(а₁, а₂,.... а_k) = 1. Целые чис­ла а и b называются взаимно простыми, если НОД(а, b)=1.

Определение 1.8. Целые числа а₁ а₂, .... a_k называются по­парно взаимно простыми, если НОД(a_i, а_j)= 1 для всех 1 ≤ i≠j ≤ k.

Взаимно простые числа обладают следующими свойствами.

1. Для того чтобы целые числа а₁, а₂, .... a_k были взаимно просты­ми в совокупности, необходимо и достаточно, чтобы существовали та­кие целые числа с₁, с₂,…с_k, что c₁a₁ + c₂a₂ + ... + с_kа_k⁼ 1

Доказательство. Необходимость следует из теоремы о существо­вании и линейном представлении наибольшего общего делителя. Дока­жем достаточность. Пусть целые числа с₁,c₂…с_k таковы, что c₁a₁ + c₂a₂ + ... + с_kа_k⁼1 и пусть d= НОД(a₁ ,a₂,…, a_k). Тогда, по опре­делению наибольшего общего делителя, каждое из чисел а₁, а₂, ..., а_к делится на d. Значит, по свойству 2 делимости, и сумма c₁a₁ + c₂a₂ + ... + с_kа_k делится на d, то есть 1 делится на d, следовательно, по свойству 6 делимости, d = 1. Таким образом, 1 = НОД(a₁, а₂,..., а_k) и числа a_i взаимно просты в совокупности.

1’. Для того чтобы целые числа а, b были взаимно простыми, необ­ходимо и достаточно, чтобы существовали такие целые числа m, п, что та + nb = 1.

2. Пусть произведение ab делится на с и НОД(а, с) = 1. Тогда b де­лится на с.

Доказательство. Числа а и с взаимно просты, тогда, по свойству 1’, существуют такие целые числа т, n, что та + пс =1. Домножим обе части последнего равенства на b:

mab + ncb = b.

Первое слагаемое в левой части равенства делится на с по усло­вию. Второе слагаемое, очевидно, делится на с. Значит, и b делится на с.

□

3. Если НОД(а, b) = 1, НОД(а, с) = 1, то НОД(a, bс) = 1.

Доказательство. Числа а и b взаимно просты, поэтому по свойст­ву 1' число 1 можно представить в виде 1 = та + пb, где числа т и n це­лые. Умножим обе части этого равенства на с, получим

с = mac + nbc.

Пусть d — наибольший общий делитель чисел а и bc. Тогда оба слагаемых в правой части равенства делятся на d, а значит и число с де­лится на d. Но 1 — наибольший общий делитель чисел а и с, то есть 1 делится на d и d= 1. □

4. ^{Если НОД(a,b1)=1, НОД(а,b2)=1, .... НОД(а,bk)=1, то}

НОД(а,b₁b₂..b_k)= 1.

5. Пусть целые числа а₁, а₂, .... а_l, b₁, b₂, .... b_k таковы, что НОД(а_i,b_j)=1 для всех 1≤ i≤ l, 1≤ j≤ k. Тогда НОД(a₁a₂..a_l,b₁,b₂...b_k)=1.

5. Пусть целое число а делится на b₁ и на b₂, НОД(b₁ b₂) = 1. Тогда a делится на произведение b₁b₂.

Доказательство. Число а делится на b₁ поэтому существует такое целое число с, что a = cb₁.

Так как а делится на b₂. то произведение cb₁ делится на b₂ Но по­скольку НОД(b₁ b₂) = 1, значит, по свойству 2 взаимно простых чисел, с делится на b₂, то есть существует такое целое число d. что с = db₂. Отсю­да а = cb₁ = db₁b₂, то есть а делится на b₁b₂, □

7. Если а делится на каждое из попарно взаимно простых чисел b₁, b₂,...b_k, то а делится на произведение b₁b₂...b_k.

Определение 1.9. Целое число М называется наименьшим общим кратным целых чисел а₁, а₂,…,а_k, аi≠0 для i=1, 2, .... k (обозначается М=НОК(a₁, а₂, .... a_k)), если выполняются следующие усло­вия:

1. М делится на каждое из чисел а₁,а₂, ....a_k;

2. если M_t — другое общее кратное чисел a_1, а₂,.... a_k, то M_t делится на М.

Наибольший общий делитель и наименьшее общее кратное двух положительных целых чисел связаны соотношением:

НОД(а, b) • НОК(а, b) = аb.