Циркуляция векторного поля

Пусть в области задано непрерывное векторное полеи ориентированная гладкая кривая(с заданным направлением обхода). Обозначим единичный вектор касательной к линиичерез, направление которого совпадает с выбранным направлением на линии.Определение. Линейным интегралом векторного поля вдоль линииназывается криволинейный интеграл 1 рода от скалярного произведения векторови:

,

где – дифференциал длины дуги кривой. Если ввести в рассмотрение вектор(здесь– радиус вектор точки, описывающий линию) и обозначить его проекции на координатные оси через, то предыдущую формулу можно записать в виде

,

где вектор направлен по касательной к. Правая часть последнего равенства является криволинейным интегралом 2 рода. Если– силовое поле, то линейный интеграл равен работе, которую поле совершает по перемещению материальной точки вдоль ориентированной линии.Определение. Линейный интеграл называется циркуляцией векторного поля , если– замкнутая линия.

Если – замкнутая пространственная кривая, то ее направление обхода специально оговаривается.Пример. Вычислить циркуляцию векторного поля по замкнутой линии, состоящей из одного витка винтовой линииот точкидо точкии прямолинейного отрезка.Решение. Виток соответствует изменению параметрав уравнениях кривой отдо. Прямаяимеет направляющий вектор, поэтому ее параметрические уравнения будут, гдеизменяется отдо. Вычислим циркуляцию как сумму криволинейных интегралов по дуге винтовой линии и по прямолинейному отрезку:.Ответ: .Вопрос. Циркуляция векторного поля по замкнутому контуру, где, может быть вычислена по формуле:

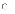
Ротор

Определение. Если векторное поле имеет дифференцируемые в точкесоставляющие, торотором (или вихрем) векторного поля в точкеназывается вектор

,

где частные производные вычислены в этой точке. В символической форме имеет вид:

.

Поясним физический смысл ротора векторного поля. Рассмотрим векторное поле как поле скоростей движущейся жидкости. Поместим в таком потоке, в определенной его точке, бесконечно малое колесико с лопастями, расположенные по окружности этого колесика. Под воздействием потока жидкости такое колесико будет вращаться с некоторой скоростью, зависящей от направления оси колесика.

Выберем систему координат так, чтобы его ось колесика совпадала бы с осью . Найдем ротор поля линейных скоростейтвердого тела, вращающегося вокруг осис постоянной угловой скоростью, причем.

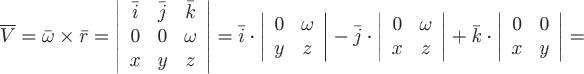
Тогда линейная скорость вращения тела будет равна: , где– радиус вектор точки. Тогда по определению ротора получим (здесь определитель раскрываем по первой строке):. С точностью до постоянного множителя ротор поля скоростейпредставляет собой угловую скорость вращения твердого тела, т.е. он характеризует "вращательную компоненту" поля скоростей. С этим связано само название «ротор» (от латинского «вращатель»). Направление ротора совпадает с направлением наибольшей плотности циркуляции.Вопрос. Вторая координата ротора векторного поля равна (введите с клавиатуры только число)

Ваш ответ

0

Формула Стокса

Если функции дифференцируемы в областии в этой области расположен некоторый замкнутый контур, то для любой незамкнутой поверхности, имеющей границу, имеет местоформула Стокса:

,

где на берется та сторона, в точках которой вектор нормалинаправлен так, чтобы видимый с его конца обход контурасовершался бы против часовой стрелки (ориентация поверхности согласована с обходом контура). Формула Стокса позволяет свести вычисление циркуляции векторного поляпо контурук вычислению потока полячерез незамкнутую поверхность, опирающуюся на контур(здесь– граница незамкнутой поверхности). Заметим, что– любая поверхность, имеющая границей контур, поэтому возможен наиболее простой ее выбор. Если через контурпровести две поверхностии, то

.

Учитывая, что иограничивают некоторую пространственное телои, меняя направление нормали на поверхностина противоположное, т.е. на внешнее по отношению к, получим

,

т. е. поток вихря через замкнутую поверхность равен . Это означает, что поле вихря является соленоидальным. Пример. Найти по формуле Стокса циркуляцию векторного поля по линиипересечения с координатными плоскостями той части поверхности, которая лежит в 1 октанте, т.е..

Решение. Находим ротор заданного векторного поля: Пусть поверхностью с границейявляется поверхность. Она является эллиптическим параболоидом и расположена в первом октанте. Вычислим циркуляцию:. Нормаль к поверхностиравна. Тогда единичная нормаль имеет координаты:. Откуда. В данном случае, т.к.в первом октанте. При этом скалярное произведение векторовиравно:. Отсюда по формулеполучим:.Ответ: .Вопрос. Используя формулу Стокса, циркуляцию векторного поля по линии пересечения параболоидас координатной плоскостьюможно свести к вычислению интеграла: