Поток векторного поля

Пусть в поле вектора задана ориентированная поверхность. Обозначим черезединичный вектор нормали к выбранной стороне поверхности в ее произвольной точке. Если для наглядности считать, что вектор- вектор скорости несжимаемой жидкости, движущейся стационарно, а поверхностьнаходится в этой жидкости. Подсчитаем количество жидкости, протекающей через эту поверхность за единицу времени. Для этого разобьем поверхностьнаэлементарных поверхностей,, ...,. В каждой из этих поверхностейвыберем точку, отложим от нее вектор нормали. Условимся при этом, что еслизамкнутая поверхность, тоберется по направлению внешней нормали. Если женезамкнута, то выберем произвольно направление нормалей так, чтобы они лежали по одну сторону от поверхности. Поверхностив силу их малости можно считать плоскими, а векторпостоянным во всех точкахи равным.

Поэтому количество жидкости , протекающей через поверхность, будет приблизительно равно объему цилиндрической фигуры с основаниеми и образующей, т.е.

,

где - проекция векторана нормальи- площадь поверхности. Общее количество жидкости, протекающей через поверхностьв единицу времени, равно сумме количеств жидкости, протекающей через все элементарные поверхности. Поэтому будем иметь:Если существует предел полученных интегральных сумм при неограниченном увеличении числа элементов разбиения поверхностии при стремлении диаметра разбиения (т.е. наибольшего размера поверхностей, входящих в разбиение) к нулю, то он является поверхностным интегралом функциипо поверхностии обозначается.Определение. Поверхностный интеграл 1 рода по поверхности от скалярного произведения векторана векторназываетсяпотоком векторного поля через ориентированную поверхность и обозначается:

В случае замкнутой поверхности поток записывается в виде. Если ввести в рассмотрение вектор и обозначить его проекции на оси координат, то формулу для потока можно переписать в виде

,

где вектор направлен по нормали к выбранной стороне поверхности. Правая часть последнего равенства является поверхностным интегралом2 рода. Если, например, – поле скоростей текущей жидкости в областии– незамкнутая поверхность с выбранным направлением нормали, то потокравен количеству жидкости, проходящей в единицу времени через поверхностьв направлении вектора. Если– замкнутая поверхность, ограничивающая некоторую областьс внешней нормалью, то потокравен разности количеств втекающей в эту область жидкости и вытекающей. В случае, если поток, то в областиимеются источники (где векторные линии порождаются), а если, то это указывает на наличие в областистоков (где векторные линии заканчиваются). А если, тогда либо нет ни источников ни стоков, либо источники и стоки уравновешивают друг друга. Если ориентированная поверхностьзадана явно непрерывно дифференцируемой функцией, где, то можно получить следующую формулу, связывающую поверхностный интеграл по поверхностис двойным интегралом по проекцииэтой поверхности на плоскость:

,

где знак «плюс» берется, когда угол острый. Если поверхностьзадана явно уравнением, гдеили, где, то соответственно меняются роли переменных в последней формуле.Пример. Найти поток векторного поля через часть поверхности параболоида, отсеченной плоскостью, если нормальк заданной поверхности составляет тупой угол с осью аппликат.Решение. Поток векторного поля будем искать по формуле, где– единичный вектор нормали к заданной поверхности, угол, область– проекция поверхностина плоскость.

Для поверхности илинормаль, тогда единичный вектор нормали, В данном случае, т.е.(тупой угол). Найдем скалярное произведение:. Т.к. проекцией заданной поверхностина плоскостьявляется круг радиуса(потому что), то при вычислении соответствующего двойного интеграла необходимо будет перейти в ПСК (полярную систему координат). Вычислим требуемый поток векторного поля:ПСК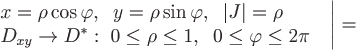.Вопрос. Поток векторного поля через часть плоскости, лежащей в первом октанте, т.е. при, (нормальсоставляет острый угол с осью)

выражается формулой