Билет№22

7.Формальная модель шифра перестановки.

Криптография защищает информацию с помощью шифрования, процедуры, исполняющей некоторое обратимое преобразование. При этом преобразовании открытого текста в шифрованный текст называется зашифрованием, а обратное преобразование - расшированием.

Шифрование предполагает наличие множества обратимых преобразований. Выбор преобразования из указанного множества для зашифрования данного сообщения осуществляется с помощью ключа. Имеется однозначное соответствие между множеством ключей и множеством преобразований. Выбор ключа естественным образом определяет функцию, вообще говоря многозначную, отображающую множество возможных открытых текстов во множество возможных шифрованных текстов. Способ вычисления значений этой функции для произвольного аргумента будем называть правилом зашифрования. Выбранный ключ будем называть ключом зашифрования. Требования однозначности расшифрования определяет обратную функцию, отображающую множество возможных (при выбранном ключе) шифрованных текстов в множество восстановленных открытых текстов. Способ вычисления значений этой функции для произвольного аргумента будем называть правилом расшифрования. Ключ, определяющий выбор правила расшифрования будем называть ключом расшифрования.

Формализуем сказанное.

Пусть - конечное множество возможных открытых текстов, ключей и шифрованных текстов соответственно;

- правило зашифрования на ключе.

Множество обозначим через, а множествообозначим через.

Пусть есть правило расшифрования на ключе, и- множество.

Будем предполагать, что представляется в виде, где- ключ зашифрования,- ключ расшифрования, причем. Тогдапонимается как функция, а- как.

Определение 1.Шифром (шифр-системой) назовем совокупность множеств, для которых выполняются следующие свойства:

5. Для любых ивыполняется;

6. .

Неформально шифр – совокупность множеств возможных открытых текстов, возможных ключей, возможных шифр-текстов, правил зашифрования и расшифрования.

Условие (1) отвечает требованию однозначности расшифрования.

Условие (2) означает, что любой элемент может быть представлен в видедля подходящих элементови.

В общем случае, утверждение, что для любых ивыполняется равенство, является неверным. Легко проверить, что из условия (1) следует свойство инъективности функции, т.е. если, причем, то.

Определение (1) вводит математическую модель, отражающую основные свойства реальных шифров. В связи с этим будем отождествлять реальный шифр с его моделью, которую будем называть алгебраической моделью шифра. Для подавляющего большинства известных шифров можно составить такую модель.

Введем вероятностную модель шифра.

Определим априорное распределение вероятностей на множествахисоответственно. Тем самымопределена вероятностьиопределена вероятность. Причем выполняется следующее равенство,.

В тех случаях, когда нам требуется знание распределений и, мы будем пользоваться вероятностной моделью, состоящей из пяти множеств, связанных условиями (1) и (2) определения (1) и двух вероятностных распределений.

В большинстве случаев множества ипредставляют собой объединение декартовых степеней некоторых множествисоответственно так, что бы для некоторых натуральныхиимеем,. Множествоиназывают соответственно множеством алфавита открытого текста и шифрованного текста.

Определим еще один шифр, называемый шифром перестановки.

Рассмотрим пример ассиметричного шифра. Для этого рассмотрим определение шифра RSA.

Определение 4.Пусть, гдеи- простые числа. Пусть- кольцо вычетов по модулю. Положим, где- функция Эйлера.

Представим ключв виде, где, а- ключи зашифрования и расшифрования соответственно. Тогда правила зашифрования и расшифрования шифраRSAопределяется дляи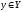формулами

(2)

Корректность формулы (2) следует из малой теоремы Ферма.