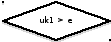Курсовая Петя
.docМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
Рязанский государственный радиотехнический университет
Кафедра радиоуправления и связи
Пояснительная записка к курсовой работе по дисциплине
«Основы вычислительной математики»
Выполнил:
студент гр. 217
Сконников П.Н.
Проверил:
Покровский П.С.
Рязань 2012
Содержание.
Цель работы…………………………………………………………….…..…
Математическая модель радиосигнала………………………………..…….
Измеряемые параметры сигнала………………………………………..…...
Блок-схема программы…………………………………………………….…
Результат работы программы………………………………………….…...
Листинг программного кода……………………………………………..….
Цель работы:
освоение и практическое применение методов вычислительной математики для решения задачи цифрового синтеза сигналов радиотехнических систем.
Задание:
1) при помощи методов вычислительной математики разработать программную реализацию (язык программирования С) алгоритма цифрового синтеза радиосигнала с нелинейной частотной модуляцией;
2) при помощи методов вычислительной математики (язык программирования С) разработать программную реализацию алгоритма определения основных параметров радиосигнала с нелинейной частотной модуляцией;
Задание выполняется на языке программирования С, трансляция текста программы в машинный код осуществляется при помощи бесплатно распространяемого компилятора «G++» версии 4.5.1. При написании программного кода рекомендуется использовать текстовый редактор «Notepad2» версии 4.2.25. Данный текстовый редактор имеет настраиваемую подсветку синтаксиса различных языков программирования.
Математическая модель радиосигнала
Радиосигналы с нелинейной частотной модуляцией широко применяются при решении радиолокационных задач, обеспечивая высокую разрешающую способность и точность проводимых измерений. В общем случае радиосигналы описываются выражением
![]() ,
,
![]() ,
,
где
![]() – закон изменения амплитуды,
– закон изменения амплитуды,
![]() – частота несущего колебания,
– частота несущего колебания,
![]() – закон изменения мгновенной частоты
радиосигнала.
– закон изменения мгновенной частоты
радиосигнала.
На практике зачастую используются радиосигналов с колоколообразной огибающей. При этом закон изменения амплитуды описывается выражением:
![]() .
.
Здесь
![]() – положительные числа, определяющие
соответственно энергию и длительность
радиосигнала. Под длительностью T
радиосигнала в данном случае понимается
время, в течение которого уровень
амплитуды радиосигнала превышает 10 %
от максимально возможного значения.
(см. рисунок 1, где
– положительные числа, определяющие
соответственно энергию и длительность
радиосигнала. Под длительностью T
радиосигнала в данном случае понимается
время, в течение которого уровень
амплитуды радиосигнала превышает 10 %
от максимально возможного значения.
(см. рисунок 1, где
![]() – общая длительность радиосигнала).
– общая длительность радиосигнала).

-
1 – Определение длительности радиосигнала
В качестве закона изменения мгновенной частоты будем рассматривать функцию вида:
![]() ,
,
где
![]() – девиация частоты радиосигнала,
– девиация частоты радиосигнала,
![]() – частота модулирующей функции.
– частота модулирующей функции.
Формирование
радиосигнала при помощи ЭВМ возможно
только в цифровом виде. При этом искомый
аналоговый радиосигнал представляется
в виде последовательности цифровых
отсчетов
![]() :
:
![]() ,
,
![]() ,
,
где
![]() – общее число отсчетов цифрового
сигнала;
– общее число отсчетов цифрового
сигнала;
![]() – период дискретизации, однозначно
связанный с частотой дискретизации
соотношением вида:
– период дискретизации, однозначно
связанный с частотой дискретизации
соотношением вида:
![]() .
.
Данный процесс иллюстрируется на рисунке 2.

-
2 – Представление радиосигнала в цифровом виде
Максимальная амплитуда А0=1.25.
Длительность радиосигнала Т =5.5 мс.
Частота модулирующей функции Ω=2.0/Тс.
Девиация частоты радиосигнала Δf=0.02f0.
Несущая частота f0=10 кГц.
Общая длительность радиосигнала Тс=15 мс .
Измеряемые параметры радиосигнала
Под измеряемыми параметрами радиосигнала с нелинейной частотной модуляцией будем понимать следующие величины: энергию сигнала, эффективную длительность и энергию производной радиосигнала.
Энергия радиосигнала определяется формулой:
![]() .
.
Эффективная длительность радиосигнала описывается выражением:
![]() ,
,
где
![]() .
.
Энергия производной радиосигнала вычисляется по формуле:
![]() ,
,
где
![]() .
.
Блок-схема программы
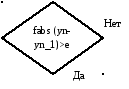
Блок-схема для функции «fabs» (Модуль)



 х
типа double
х
типа double
Да
Нет


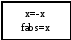





Fabs
Блок-схема для функции «sqrt» (Квадратный корень)

х типа double
Нет
1
3
2
Да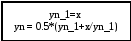
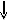
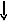
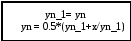




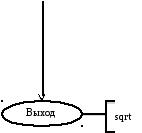




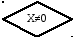




1 – установка начальных параметров.
2 – сравнение текущей поправки с заданной погрешностью.
3 – вычисление текущей итерации.
Блок-схема для функции «cos» (Косинус)










да
нет