Нелинейная оптимизация. Метод Нелдера-Мида

Константин Ловецкий Кафедра телекоммуникаций Сентябрь, 2012

Цель проекта

•Разработка и внедрение программы минимизации функций

•Приемы программирования

Историческая справка

•Симплекс-метод Нелдера-Мида, впервые опубликованный в 1965 году, неимоверно популярен в качестве метода прямого поиска решения в задачах многомерной оптимизации без ограничений. Однако, несмотря на широкое распространение метода, теоретические

результаты о его сходимости практически отсутствуют.

•Рассмотрим сходимость этогометода для строго выпуклых функций в пространствах размерности 1 и 2 по материалам статьи авторов, работающих в AT&T Labs-Research, Florham Park, NJ 07932 и Bell Laboratories, Murray Hill, NJ 07974

•Докажем сходимость метода к минимуму в пространстве размерности 1 и несколько более слабых результатов о сходимости в пространстве размерности 2. Контрпример МакКиннона (McKinnon) показывает, что существует семейство строго выпуклых функций в пространстве размерности 2 и существуют множества начальных условий, при которых метод Нелдера-

Мида не сходится к точке минимума. Поэтому остается открытым вопрос, можно ли доказать сходимость метода для некоторого специального, но достаточно широкого класса выпуклых функций даже в двухмерном пространстве.

•JEFFREY C. LAGARIAS, JAMES A. REEDS, MARGARET H. WRIGHT, AND PAUL E. WRIGHT.

•NELDER-MEAD SIMPLEX METHOD IN LOW DIMENSIONS

•SIAM J. OPTIM. °c 1998 Society for Industrial and Applied Mathematics

•Vol. 9, No. 1, pp. 112-147

Историческая справка

Метод впервые был опубликован в работе J. A. Nelder and R. Mead, A simplex method for function minimization, Computer Journal 7 (1965), 308-313.

С моментапервой публикации симплекс метод Нелдера и Мида стал одним из наиболее популярных методов решения задач многомерной минимизации без ограничений. Сам метод не надо путать с (возможно) более известным методом Данцига (Dantzig) решения задач линейного программирования; оба метода при решении задач используют последовательность симплексов, однако на этом их сходство заканчивается.

Метод Нелдера-Мида предназначен исключительно для решения задач минимизации без ограничений.

Историческая справка

Метод активно используется при решенииприкладных оптимизационных задач в таких областях, как инженерная химия и медицина. Особую популярностьметод приобрел после появления его описания в известной книге Numerical Recipes, где он появился под названием «амеба-алгоритм» и в пакете Matlab.

Алгоритм Нелдера-Мида

Алгоритм Нелдера-Мида минимизирует скалярную нелинейную функцию n действительных переменных используя лишь вычисление значений функции и не используя информацию о ее производных (явно либо неявно). Тем самым метод попадает в общий класс прямых методов поиска.

Большой подкласс таких методов, включая и метод Нелдера- Мида, опирается на вычисление на каждом шаге невырожденного симплекса, геометрической фигуры ненулевого объема в n-мерном пространстве, являющейся выпуклой оболочкой n + 1 вершины.

Алгоритм Нелдера-Мида

Обычно метод, базирующийся на итерациях на основе симплекса, начинает с определения самого симплекса и определения его (n+1)-ой вершины, а также вычисления

соответствующих этим вершинам значений функции. Затем вычисляются одна или несколько пробных вершин и значений функции в них. Переход к новой итерации осуществляется после замены одной из предыдущих вершин новой вершиной.

Итерации прекращаются по достижении заданной точности (определяется как по разности значений функции, так и по объему многогранника – симплекса).

Алгоритм Нелдера-Мида

Итак, метод Нелдера-Мида минимизации функции f (x), x Rn определяется четырьмя скалярными параметрами:

коэффициентами

отражения ( ), растяжения( ), сжатия ( ),

Обычно в стандартной реализации алгоритма выбирают

1, 2, 1/ 2, 1/ 2.

Одна итерация метода

• 1. Упорядочивание. Сортировкаn + 1 вершины

так, что f(x1) ≤ f(x2) ≤… ≤ f(xn+1);

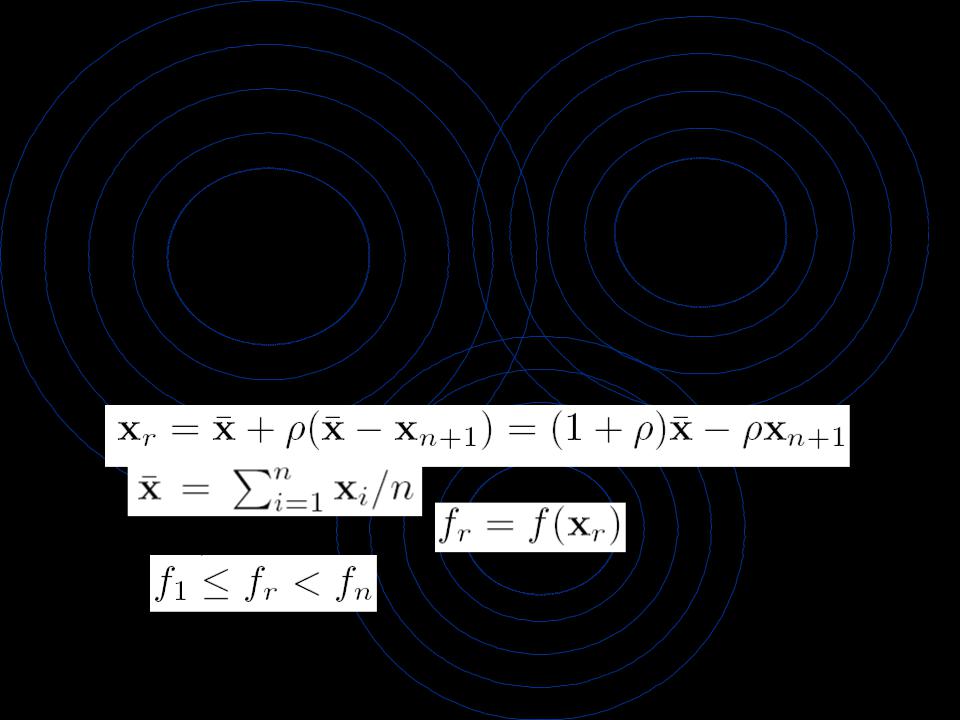
•2. Отражение. Вычислить точку отражения по формуле

отражения и закончить итерацию.