
- •Учебное пособие
- •Тема. Комбинаторика
- •Биномиальные коэффициенты
- •Бином Ньютона
- •Треугольник Паскаля
- •Разбиения множества
- •Числа Стирлинга второго рода
- •Число Белла
- •Числа Стирлинга первого рода
- •Формулы включений и исключений
- •Лекция 5. Производящие функции. Основные операции. Примеры использования.
- •Производящие функции
- •Основные операции
- •Примеры использования ПФ
- •Лекция 6. Генерирование комбинаторных объектов. Перестановки. Сочетания. Разбиение чисел. Подмножества множеств.
- •Перестановки
- •Сочетания
- •Разбиения чисел
- •Подмножества множества
- •Тема. Теория конечных графов
- •Ребро
- •Цвет
- •Букет
- •Букет
- •Пуст
- •Лекция 1. Введение в комбинаторику.
- •Некоторые области применения задач комбинаторики.

В. Ни одна из концевых вершин не принадлежит ни одному из сформированных букетов. Если имеет место такой случай, то необходимо окрасить ребро в синий цвет и сформировать новый букет из его концевых вершин.
Г. Концевые вершины выбранного ребра принадлежат различным букетам. В этом случае необходимо окрасить выбранное ребро в синий цвет, а оба букета, которым принадлежат его концевые вершины, слить в один новый букет.
Шаг 3. Если все вершины графа вошли в один букет, закончить процедуру, так как при этом условии голубые ребра образуют покрывающее дерево. В противном случае вернуться к началу шага 2.
Пример 10.1.
|
|
Ребро |
Цвет |
Букет |
Букет |
|
a |
b |
№ 1 |
№ 2 |
|||
|
|
|||||
|
|
Пуст |
Пуст |
|||
|
|
|
|
|||
c |
|
(a,b) |
Синий (1) |
{a,b} |
Пуст |
|
|
(d,e) |
Синий (2) |
{a,b} |
{d,e} |
||
|
|
|||||
d |
e |
(a,d) |
Синий (3) |
{a,b,d,e} |
Пуст |
|
(b,e) |
Оранжевый |
{a,b,d,e} |
Пуст |
|||
|
|
|||||
|
|
(e,c) |
Синий (4) |
{a,b,d,e,c} |
Пуст |
В таблице показаны этапы построения покрывающего дерева. Ребра графа рассматриваются в следующем произвольно выбран-
ном порядке: (a,b), (d,e), (a,d), (b,e), (e,c), (c,b), (a,c) и (с,d). Алго-
ритм заканчивается просмотром ребра (e,c), поскольку после этого вершины рассматриваемого графа попадают в один букет. Четыре голубых ребра (a,b), (d,e), (a,d) и (e,c) образуют для данного графа покрывающее дерево (на рисунке ребра этого дерева выделены).
Рассмотренный алгоритм не учитывает веса ребер. Для решения задачи о слухах и аналогичных ей это и не нужно, так как в этом случае достаточно ответить на вопрос, связен граф или нет. К вопросу связности орграфов мы вернемся в лекции 14.
Лекция 11. Поиск на графах : алгоритмы поиска в глубину и в ширину.
При решении прикладных задач часто возникает необходимость обхода вершин графа, связанная с поиском вершин, удовлетворяющих определенным свойствам. Например, необходимо от-
39
ветить на вопрос: достижима ли вершина d из вершины v, то есть, существует ли путь из v в d. Если исходный граф неориентированный, то для ответа на данный вопрос достаточно определить принадлежат ли вершины v и d одному компоненту связности. Выделить связные компоненты можно с помощью алгоритма Краскала. Если после завершения работы алгоритма Краскала вершины v и d принадлежат разным деревьям покрывающего леса (разным букетам – в терминах, используемых при формулировке алгоритма Краскала), то пути из вершины v в вершину d не существует, в противном случае путь существует.
Для ориентированного графа такой алгоритм непригоден. Для ответа на вопрос достижима ли вершина d из вершины v, необходимо организовать обход вершин графа, начиная из вершины v. Если во время обхода мы встретим вершину d, следовательно, вершина d достижима из вершины v, в противном случае d из v не достижима.
Существует два способа организации обхода: поиск в глубину и поиск в ширину. Просмотр всех вершин графа G=(V,E), V={v1,…,vn} осуществляется так, что каждая вершина рассматривается один раз.
Поиск в глубину
Обозначения: new[1..n] - массив булевых переменных,
true,еслиv непросматривалась, new[ v ] =
false,еслиv просматривалась;
U[1…n] -массив указателей на списки инцидентности вершин графа;
stack -стек (LIFO - last-in-first-out) емкости n.
Алгоритм поиска в глубину (в круглых скобках даны комментарии).
procedure DFS[v]- процедура поиска в глубину (depth first search), начиная с вершины v.
begin
stack:=0; stack ←v; рассмотреть v; new[v]:=false;
while stack ≠ 0 do begin
t:= top(stack); (верхний элемент стека) if U[t]=nil then b:=false
40
else b:=not new [U[t]↑.dat]; while b do
begin U[t]:=U[t]↑.next;
if U[t]=nil then b:=false
else b:=not new [U[t]↑.dat]
end;
if U[t]≠nil then (найдена новая нерассмотренная вершина)
begin
w:=U[t]↑.dat; stack ←w; рассмотреть w; new[w]:=false
end;
else (вершина t рассмотрена)
t←stack (удалить верхний элемент стека)
end
end
Пояснение к алгоритму. Начинаем из вершины v. Пусть на некотором шаге мы попали в вершину u. Идем далее из вершины u в вершину w, смежную с u. Если w уже рассматривалась, то возвращаемся в u и идем в другую смежную с ней вершину. Если же w еще не рассматривалась, то применяем к ней описанную выше процедуру. Процесс завершается при попытке вернуться назад из начальной вершины v.
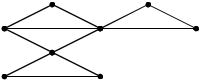
Пример 11.1. Пояснения к алгоритму будем давать на примере графа, изображенного на рисунке.
|
2 (2) |
7 (7) |
Порядок прохождения |
1 (1) |
|
|
|
|
6 (3) |
8 (8) |
вершин указан на рисунке |
3 (4) |
в круглых скобках рядом с |
||
|
|
номером вершины. |
|
|
|
|
|
4 (5) |
5 (6) |
|
|
41
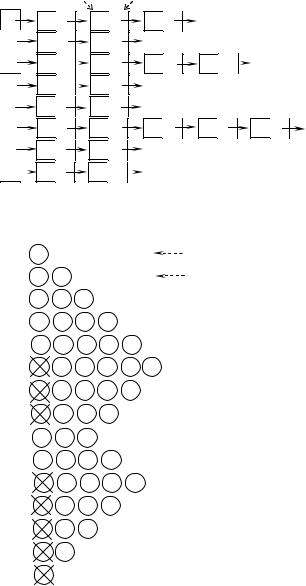
Массив U указателей для этого графа будет иметь вид
U |
|
dat |
next |
|
|
|
1 |
2 |
3 |
6 |
nil |
|
|
2 |
1 |
6 |
nil |
|
|
|
3 |
1 |
4 |
5 |
6 |
nil |
|
4 |
3 |
5 |
nil |
|
|
|
5 |
3 |
4 |
nil |
|
|
|
6 |
1 |
2 |
3 |
7 |
8 |
nil |
7 |
6 |
8 |
nil |
|
|
|
8 |
6 |
7 |
nil |
|
|
|
На каждом шаге содержимое стека (массив stack) указывает маршрут от исходной вершины до рассматриваемой.
stack |
1 |
|
|
|
|
1-й шаг |
|
2 |
1 |
|
|
|
2-й шаг |
|
6 |
2 |
1 |
|
|
. |
|
|
|
. |
|||
|
|
|
|
|
|
|
|
3 |
6 |
2 |
1 |
|
. |
|
4 |
3 |
6 |
2 |
1 |
|
|
5 |
4 |
3 |
6 |
2 |
1 |
|
4 |
3 |
6 |
2 |
1 |
|
|
3 |
6 |
2 |
1 |
|
|
|
6 |
2 |
1 |
|
|
|
|
7 |
6 |
2 |
1 |
|
|
|
8 |
7 |
6 |
2 |
1 |
|
|
7 |
6 |
2 |
1 |
|
|
|
6 |
2 |
1 |
|
|
|
|
2 |
1 |
|
|
|
|
|
1 |
|
|
|
|
|
42
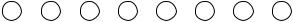
Замечание. Перечеркивание вершины на рисунке обозначает удаление соответствующей вершины из стека (это происходит в случае, когда в стек попадает уже рассмотренная ранее вершина).
Ниже приведено содержимое массива new. Верхняя строка дает исходное состояние. В нижней строке указан порядок изменения состояния элементов массива (ср. с рисунком графа).
new |
T |
T |
|
T |
|
T |
T |
T |
T |
T |
|
|
|
||||||||
|
(true) |
|
|
|
|
|
|
|
|
|
|
F 1 |
F 2 |
F 4 |
F 5 |
F 6 |
F 3 |
F 7 |
F 8 |
||
|
(false) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
3 |
4 |
5 |
6 |
7 |
8 |
Поиск в ширину в графе
Вместо стека в данном алгоритме используется очередь. Обозначения: prev[1..n] - вспомогательный массив;
queue - очередь (FIFO - first-in-first-out) емкости n.
Алгоритм поиска в ширину (в круглых скобках даны комментарии).
procedure BFS(v)- процедура поиска в ширину (breadth first search), начиная с вершины v
begin
queue:=0; queue←v; new[v]:=false; while queue≠0 do
begin
p←queue; (извлечь из очереди вершину), рассмотреть p; while U[p}≠nil do
begin
if new [U[p]↑.dat] then begin
queue←U[p]↑.dat; new[U[p]↑.dat]:=false; prev[U[p]↑.dat]:=p;
end; U[p]:=U[p]↑.next;
end;
end;
end;
43
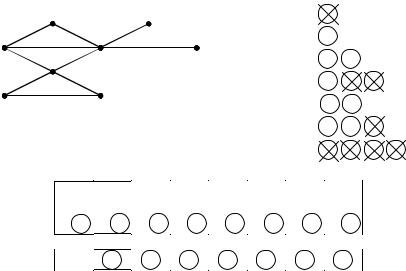
Ниже на рисунке указан порядок прохождения вершин при поиске в ширину для графа из примера 11.1, а также приведено содержимое массивов queue, new, и prev .
|
2 (2) |
|
7 (7) |
|
|
queue 1 |
|
|
|
|
|
1 (1) |
|
|
|
|
|
|
2 |
|
|
|
|
3 (3) |
|
6 (4) |
|
8 (8) |
|
|
3 |
|
2 |
|
|
|
|
|
|
|
|
6 |
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
4 (5) |
5 (6) |
|
|
|
|
4 |
6 |
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
5 |
|
4 |
6 |
|
|
|
|
|
|
|
|
8 |
|
7 |
5 |
4 |
new |
T |
T |
T |
T |
T |
T |
T |
T |
|
|
|
|
F 1 |
F 2 |
F 3 |
F 5 |
F 6 |
F 4 |
F 7 |
F 8 |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
prev |
1 |
1 |
3 |
3 |
1 |
6 |
6 |
|
|
|
|
Замечание. Содержимое prev[u] содержит вершину, из которой мы попали в u. Таким образом, мы имеем возможность определить кратчайший путь от начальной до нужной вершины.
Алгоритмы поиска в глубину и в ширину могут быть легко модифицированы для поиска компонентов связности графа, а также для нахождения покрывающего дерева графа. Ниже приведена процедура построения покрывающего дерева графа G=(V,E), V={v1,…,vn}, основанная на алгоритме поиска в глубину. Используем ранее введенные обозначения и пусть T - массив ветвей искомого дерева.
procedure WGD[v]- процедура поиска покрывающего дерева графа методом поиска в глубину (depth first search), начиная с вершины v.
begin
stack:=0; stack ←v; T:=0; new[v]:=false;
while stack ≠ 0 do
44
begin
t:= top(stack);
if U[t]=nil then b:=false
else b:=not new [U[t]↑.dat]; while b do
begin U[t]:=U[t]↑.next;
if U[t]=nil then b:=false
else b:=not new [U[t]↑.dat]
end;
if U[t]:≠nil then begin
w:=U[t]↑.dat; stack ←w; T:=Т {t,w}; new[w]:=false
end;
else t←stack
end
end
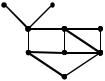
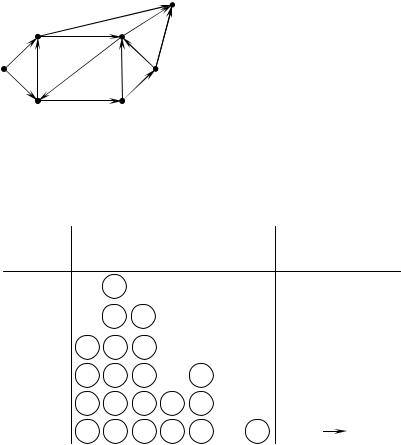
Пример 11.2. Порядок прохождения вершин при построении покрывающего дерева графа (ветви дерева выделены).
8 |
9 |
|
T=(1,2) (2,3) (3,4) (4,6) |
5 |
6 |
7 |
|
2 |
3 |
4 |
(6,5) (5,8) (5,9) (6,7) |
|
|||
|
1 |
|
|
Лекция 12. Эйлеровы графы. Алгоритм поиска эйлерова цикла в графе.
Начало теории графов как раздела математики связывают с так называемой задачей о кенигсбергских мостах.
Задача. Город Кенигсберг (Калининград) был построен на берегах и двух островах реки Преголи. В городе было семь мостов, которые соединяли острова между собой и с береговыми частями города (рис. 12.1). Можно ли, выйдя из дома, вернуться обратно, пройдя по каждому мосту только один раз? Сопоставим рисунку граф (рис. 12.2), вершины которого соответствуют четырем разде-
45
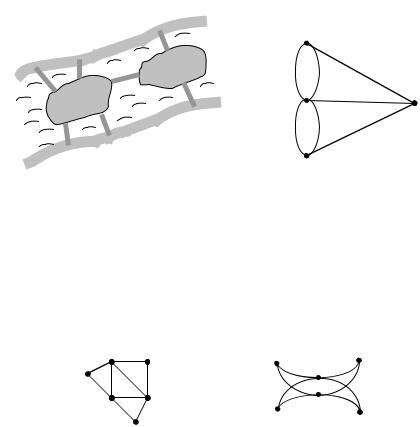
ляемым рекой участкам суши A,B,C,D, а ребра – мостам.
C
|
C |
|
D |
A |
A |
|
D |
B |
B |
Рис.12.1. |
Рис.12.2. |
Таким образом, задачу о кенигсбергских мостах можно на языке теории графов сформулировать следующим образом: есть ли в графе на рис. 12.2 цикл, содержащий все ребра графа? Эйлер доказал неразрешимость этой задачи.
Определение. Цикл в графе называется эйлеровым, если он содержит все ребра графа.
Определение. Связный граф, в котором есть эйлеров цикл, называется эйлеровым графом.
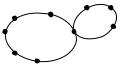
Примеры эйлеровых графов.
2 |
3 |
|
|
|
|
|
|
||
1 |
4 |
|
|
|
|
|
|
||
6 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
(1,2,3,4,2,6,4,5,6,1) |
Сабли Магомета |
|||
Теорема. Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин четны.
Доказательство.
Необходимость. Пусть G - эйлеров граф. Эйлеров цикл этого графа, проходя через каждую вершину графа, входит в нее по одному ребру, а выходит по другому. Это означает, что каждая вершина инцидентна четному числу ребер эйлерового цикла, а поскольку такой цикл содержит все ребра графа G, то отсюда следует четность степеней всех его вершин.
Достаточность. Предположим теперь, что степени всех вершин графа G четны. Начнем цепь P1 из произвольной вершины v1 и бу-
46
дем продолжать ее, насколько возможно, выбирая каждый раз новое ребро. Т.к. степени всех вершин четны, попав в очередную, отличную от v1, вершину, мы всегда будем иметь в распоряжении еще не пройденное ребро. Поэтому построение цепи P1 закончится в вершине v1, т.е. P1 будет циклом. Если P1 содержит все ребра графа G, то это и будет требуемый эйлеров цикл. В противном случае, удалив из G все ребра цикла P1, получим граф G1. Т.к. P1 и G имели вершины только четных степеней, то и G1 имеет вершины только четных степеней. В силу связности графа G графы P1 и G1 должны иметь хотя бы одну общую вершину v2. Начиная с вершины v2, построим цикл P2 в графе G1 аналогично построению цикла P1 в графе G. Обозначим через P1’ и P1” части цикла P1 от v1 до v2 и от v2 до v1 соответственно (рис.12.3). Получим новый цикл P3= =P1’ P2 P1”, который, начиная с v1, проходит по ребрам цепи P1’ до v2, затем по всем ребрам цикла P2, и возвращается в v1 по реб-
P1’ |
|
|
рам цепи P1”. Если P3 не эйлеров цикл, |
v2 |
|
то повторяем предыдущую процедуру. |
|
v1 |
P2 |
Получим еще больший цикл. В силу |
|
P1” |
|
конечности графа G этот процесс за- |
|
|
|
кончится построением эйлерового цик- |
|
|
|
|
ла.
На этой идее основан алгоритм нахождения эйлерового цикла в графе.
Обозначения: G=(V,E) - связный граф без вершин нечетной степе-
ни, V={v1,…,vn};
u[v] - список инцидентности для вершины v, u[1..n]; stack - рабочий стек;
res - стек, содержащий последовательность вершин эйлерового цикла.
begin
stack:=0; res:=0;
v:= произвольная вершина графа; stack ← v;
while stack ≠ 0 do begin
v:=top (stack);
if u[v]≠ nil then
47
begin
w:=первая вершина списка u[v];
stack ← w; (удалить ребро (v,w) из графа) u[v]:=u[v]|{w};
u[w]:=u[w]\{v};
v:=w end
else
begin
v ← stack; res ← v end
end
end
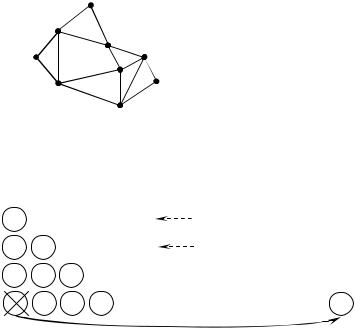
Пример 12.1. Рассмотрим работу алгоритма на примере сле-
дующего графа. |
|
|
|
u(1)={ 2,3 } |
|
|
|
|
|
|
|
|
|
u(2)={ 1,3,7,8 } |
4 |
|
|
|
u(3)={ 1,2,4,5 } |
3 |
|
5 |
|
u(4)={ 3,5 } |
|
|
6 |
u(5)={ 3,4,6,8 } |
|
|
|
|
||
1 |
8 |
|
9 |
u(6)={ 5,7,8,9 } |
2 |
|
|
7 |
u(7)={ 2,6,8,9 } |
|
|
|
u(8)={ 2,5,6,7 } |
|
|
|
|
|
u(9)={ 6,7 } |
Ниже приведено содержимое массивов stack (по шагам) и res. stack
1 |
|
1-й шаг |
2 |
1 |
2-й шаг |
3 2 1
1 |
3 |
2 |
1 |
.
.
. res 1
48
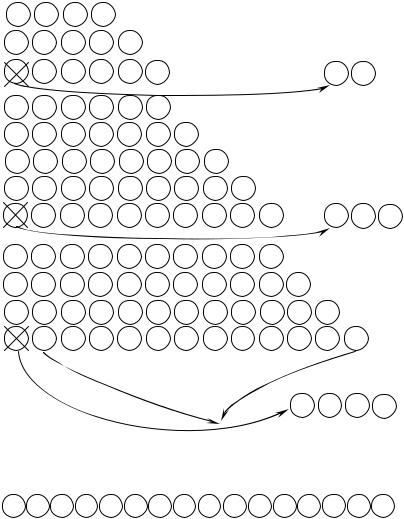
stack
4 |
3 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
5 |
4 |
3 |
2 |
1 |
|
|
|
|
|
|
|
|
|
3 |
5 |
4 |
3 |
2 |
1 |
|
|
|
|
res |
3 |
1 |
|
6 |
5 |
4 |
3 |
2 |
1 |
|
|
|
|
|
|
|
|
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
|
|
|
|
|
|
2 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
|
|
|
|
|
8 |
2 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
|
|
|
|
5 |
8 |
2 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
res |
5 |
3 |
1 |
6 |
8 |
2 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
|
|
|
9 |
6 |
8 |
2 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
|
|
7 |
9 |
6 |
8 |
2 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
|
8 |
7 |
9 |
6 |
8 |
2 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
. . . |
res 8 |
5 |
3 |
1 |
|
res 
1 2 3 4 5 6 7 2 8 6 9 7 8 5 3 1
Замечание. Эйлеровым путем в графе называется произвольный путь, проходящий через каждое ребро графа точно один раз.
Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более чем две вершины нечетной степени.
49
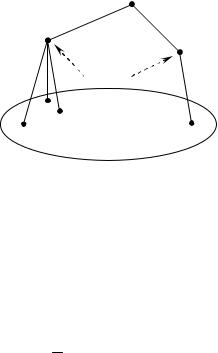
Эйлеров путь начинается в одной из вершин с нечетной степенью и заканчивается в другой вершине с нечетной степенью.
|
|
t |
|
Пояснение: Добавляем |
|
|
|
вершину t и соединяем ее |
|
|
|
|
|
|
u |
|
|
|
с u и v. В новом графе |
вершины |
|
v |
степени всех вершин чет- |
|
|
|
ны и его эйлеровы циклы |
||
|
нечетной |
|
|
|
|
степени |
|
|
находятся во взаимно од- |
|
|
|
|
нозначном соответствии с |
|
|
|
|
эйлеровыми путями ис- |
|
граф G |
|
|
ходного графа. |
|
|
|
|
Лекция 13. Нахождение пути наименьшей длины в графе. Алгоритм Дейкстра.
Пусть G=<V,E> - орграф без петель, V={v1,…,vn}. Каждой дуге <vi,vj> поставлено в соответствие некоторое действительное число wij, wij≥ 0 , называемое весом (или длиной) дуги.
В реальной жизни вес дуги может означать стоимость прокладки линий связи, например, между городами, обозначаемыми вершинами графа, или длину дороги и т.д.
Если дуги <vi,vj> не существует, то wij=∞. Матрица называется матрицей весов.
vi1 ,...,vir - путь в графе G. Тогда
) = wi1i2 +...+ wir−1ir - длина пути.
Часто необходимо находить путь наименьшей длины (кратчайший путь) в орграфе. Примером может служить следующая задача.
Задача. Предположим, что вам необходимо иметь в своем распоряжении автомобиль в течении нескольких лет. Имеется большой выбор автомобилей. Автомобили имеют различные сроки эксплуатации и разную стоимость. Каким образом выбрать вариант покупок автомобилей на заданном временном интервале имеющий минимальную суммарную стоимость покупаемых автомобилей?
Для того, чтобы свести данную задачу к графовой, представим моменты времени возможных сделок на заданном временном ин-
50
тервале, связанных с покупкой автомобиля, вершинами некоторого графа. Для упрощения в качестве моментов времени сделок можно рассматривать лишь первые дни каждого месяца, квартала или другого временного отрезка. Изобразим в данном графе факт приобретения автомобиля дугой, соединяющей вершину, соответствующую моменту покупки, с вершиной, соответствующей моменту окончания срока службы автомобиля. Весом дуги построенного графа является стоимость соответствующей сделки.
Чтобы выбрать вариант с минимальной суммарной стоимостью, необходимо среди всех возможных путей из вершины, соответствующей начальному моменту времени, в вершину, соответствующую конечному моменту времени, найти путь наименьшей длины.
Определение. Путь наименьшей длины между вершинами s и t будем называть расстоянием от s до t и обозначать через D(s,t).
Первый эффективный алгоритм решения задачи нахождения кратчайшего пути в графе между двумя фиксированными вершинами при условии, что все дуги графа имеют неотрицательный вес, предложил в 1959г. Е.Дейкстра.
Идея алгоритма. Нахождение расстояния от s до t начинается с вершины s и ведется методом поиска в ширину.
На каждой итерации алгоритма всякая вершина v графа G имеет метку l(v) , которая может быть постоянной или временной. Если метка l(v) является постоянной, то она равна расстоянию D(s,v) (т.е. кратчайшему пути от s до v). Если же метка l(v) временная, то l(v) - длина кратчайшего пути от s до v, проходящего через вершины с постоянными метками. Таким образом, временная метка l(v) является оценкой сверху для расстояния D(s,v) , и, став на некоторой итерации постоянной, она остается такой до конца работы алгоритма.
Кроме l(v) с каждой вершиной v графа G, за исключением s, связывается еще одна метка - θ(v). На каждой итерации θ(v) является номером вершины, предшествующей v, в пути от s до v, проходящем через вершины с постоянными метками и являющимися кратчайшим среди всех таких путей.
После того, как вершина t получит постоянную метку, с помощью меток θ(v) легко указать последовательность вершин, составляющих кратчайший путь от s до t.
Перед началом первой итерации алгоритма вершина s имеет постоянную метку l(s)=0, а метки l всех остальных вершин равны
51
∞ и являются временными. Общая итерация алгоритма состоит в следующем. Пусть p - вершина, получившая постоянную метку l(p) на предыдущей итерации. Просматриваем все вершины с временными метками, в которые идут дуги из p, (обозначим эти вершины Г(p) ) с целью уменьшения этих меток, если это возможно. Метка l(v) вершины v Г(p) заменяется на l( p ) + wp ,v , если
l(v)>l(p)+wp,v. В этом случае говорим, что вершина v получила свою метку l(v) из вершины p и полагаем θ(v)=p. Если же l(v)≤ l(p)+wp,v , то метки θ(v) и l(v) не изменяются на данной итерации. Просматриваем все v Г(p) и для вершины u Г(p) такой, что
l( p,u) = min l( p,v) считаем l( p,u) постоянной меткой. Алгоритм
v Г(p)
заканчивает работу, когда метка l(t) становится постоянной. Обозначения: last - последняя помеченная вершина;
true,еслиv имеетпостояннуюметку, fin( v ) =
false,еслиv имеетвременнуюметку;
u[v] - список инцидентов для вершины v. Алгоритм Дейкстра нахождения расстояния между фиксиро-
ванными вершинами s и t. for v V do l[v]:=∞;
for v V do fin[v]:=false; l[s]:=0;
fin[s]:=true;
last:=s;
while not fin[t] do begin
for v u [last] do
if not fin[v] and l[v]>l[last]+wlast,v then begin
l[v]:=l[last]+wlast,v; θ(v):=last
end;
for v множество вершин с временными метками do begin
определить k : l[k]=min l[v]; fin[k]:=true;
last:=k end
end
52
Замечание 1. Алгоритм применим к неориентированным графам. Достаточно заменить каждое ребро (vi,vj), имеющее вес wij, на пару дуг <vi,vj> и <vj,vi> того же веса.
Замечание 2. Алгоритм может быть использован для нахождения кратчайшего пути в графе, ребрам (дугам) которого не присвоены веса. Необходимо каждому ребру (дуге) присвоить вес, равный единице.
Пример 13.1. Найти расстояние от b до g в графе, изображенном на рисунке.
|
|
|
10 |
g |
|
a |
|
|
|
|
4 |
d |
2 |
|
7 |
|
|
6 |
|
|
8 |
|
1 f |
|
b |
4 |
3 |
||
2 |
c |
5 |
e |
7 |
|
|
|
Таблица значений меток θ(v).
|
Номер |
|
a |
b |
c |
d |
e |
f |
g |
|
|
||||||||
итерации |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
* |
|
|
|
|
|
1 |
|
b |
* |
b |
|
|
|
|
|
2 |
|
c |
* |
b |
|
c |
|
|
|
3 |
|
c |
* |
b |
a |
c |
|
a |
|
4 |
|
c |
* |
b |
e |
c |
e |
a |
|
5 |
|
c |
* |
b |
e |
c |
e |
d |
|
Таблица значений меток l(v) (постоянные метки вершин обведены).
Номер |
|
|
|
|
|
|
|
Вершина, |
|
a |
b |
c |
d |
e |
f |
g |
получившая пост. |
||
итерации |
|
|
|
|
|
|
|
метку на итерации |
|
|
|
|
|
|
|
|
|
||
0 |
∞ |
0 |
∞ |
∞ |
∞ |
∞ |
∞ |
b |
|
1 |
7 |
0 |
2 |
∞ |
∞ |
∞ |
∞ |
c |
|
2 |
6 |
0 |
2 |
∞ |
7 |
∞ |
∞ |
a |
|
3 |
6 |
0 |
2 |
10 |
7 |
∞ |
16 |
e |
|
4 |
6 |
0 |
2 |
10 |
7 |
14 |
16 |
d |
|
5 |
6 |
0 |
2 |
10 |
7 |
14 |
12 |
g |
stop |
Расстояние D(b,g)=12, путь bcedg.
53

Лекция 14. Нахождение расстояния между всеми парами вершин. Алгоритм Уоршалла-Флойда. Связность орграфов. Транзитивное замыкание.
Очевидно, что задачу определения расстояния между всеми парами вершин можно решить, используя n(n-1) раз алгоритм Дейкстра. Однако, сложность такой процедуры будет составлять O(n4). Существуют более эффективные алгоритмы, в частности, алгоритм Уоршалла и Флойда.
Рассмотрим орграф G=<V,E>, V={v1,…,vn}. Пусть W = ( wij )i , j=1,n - матрица весов графа. Пусть dij( m ) - длина кратчайшего из путей из vi в vj с промежуточными вершинами в множест-
ве {v1,…,vm}, m =1,n . Тогда
d ( 0 ) = w |
(14.1) |
||
ij |
ij |
|
|
|
|
|
|
dij( m ) = min( dij( m−1 ) ,dim( m−1 ) + dmj( m−1 ) ) , i, j,m =1,n |
(14.2) |
||
Обоснование уравнения (14.2) следующее. Рассмотрим крат-
чайший путь из vi в vj с промежуточными вершинами из множества {v1,…,vm}. Если этот путь не содержит vm, то dij(m) = dij(m-1). Если же
он содержит vm, то деля путь на отрезки от vi до vm и от vm до vj получаем равенство dij(m) = dim(m-1)+ dmj(m-1). Уравнения (14.1) и (14.2)
дают возможность вычислять расстояния D(vi,vj)=dij(n) для любых
1≤ i,j ≤ n.
Алгоритм Уоршалла-Флойда.
Здесь D(vi,vj)=D[i,j]. begin
for i=1 to n do
for j=1 to n do D[i,j]=W[i,j]; for m:=1 to n do
for i:=1 to n do for j:=1 to n do
D[i,j]:=min(D[i,j], D[i,m]+ D[m,j]
end
Сложность алгоритма Уоршалла-Флойда O(n3).
54
Пример 14.1.
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
5 |
3 |
1 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
2 |
1 |
4 |
1 |
|
W = |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
4 |
3 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D(1) |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
||||||||||||
1 |
|
|
|
|
|
|
∞ |
1 |
∞ |
∞ |
∞ |
∞ |
||
2 |
|
|
|
|
|
|
∞ |
∞ |
5 |
2 |
∞ |
7 |
|
|
3 |
|
|
|
|
|
|
∞ |
∞ |
∞ |
∞ |
∞ |
1 |
|
|
4 |
|
|
|
|
|
|
2 |
3 |
1 |
∞ |
4 |
∞ |
||
5 |
|
|
|
|
|
|
∞ |
∞ |
∞ |
3 |
∞ |
∞ |
||
6 |
|
|
|
|
|
|
∞ |
∞ |
∞ |
∞ |
1 |
∞ |
||
D(3) |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|||
|
|
|
||||||||||||
1 |
|
|
|
|
|
|
∞ |
1 |
6 |
3 |
∞ |
7 |
|
|
2 |
|
|
|
|
|
|
∞ |
∞ |
5 |
2 |
∞ |
6 |
|
|
3 |
|
|
|
|
|
|
∞ |
∞ |
∞ |
∞ |
∞ |
1 |
|
|
4 |
|
|
|
|
|
|
2 |
3 |
1 |
5 |
4 |
2 |
|
|
5 |
|
|
|
|
|
|
∞ |
∞ |
∞ |
3 |
∞ |
∞ |
||
6 |
|
|
|
|
|
|
∞ |
∞ |
∞ |
∞ |
1 |
∞ |
||
D(5) |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|||||
|
|
|||||||||||||
1 |
|
|
|
|
|
|
5 |
1 |
4 |
3 |
7 |
5 |
|
|
2 |
|
|
|
|
|
|
4 |
5 |
3 |
2 |
6 |
4 |
|
|
3 |
|
|
|
|
|
|
∞ |
∞ |
∞ |
∞ |
∞ |
1 |
|
|
4 |
|
|
|
|
|
|
2 |
3 |
1 |
5 |
4 |
2 |
|
|
5 |
|
|
|
|
|
|
5 |
6 |
4 |
3 |
7 |
5 |
|
|
6 |
|
|
|
|
|
|
6 |
7 |
5 |
4 |
1 |
6 |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
||||||
1 |
∞ |
1 |
∞ |
∞ |
∞ |
∞ |
|
2 |
∞ |
∞ |
5 |
2 |
∞ |
7 |
|
3 |
∞ |
∞ ∞ |
∞ ∞ 1 = D(0) |
||||
4 |
2 |
∞ |
1 |
∞ |
4 |
∞ |
|
5 |
∞ |
∞ |
∞ |
3 |
∞ |
∞ |
|
6 |
∞ |
∞ |
∞ |
∞ |
1 |
∞ |
|
D(2) |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
||
|
||||||||||||
1 |
|
|
|
|
|
∞ |
1 |
6 |
3 |
∞ |
8 |
|
2 |
|
|
|
|
|
∞ |
∞ |
5 |
2 |
∞ |
7 |
|
3 |
|
|
|
|
|
∞ |
∞ |
∞ |
∞ |
∞ |
1 |
|
4 |
|
|
|
|
2 |
3 |
1 |
5 |
4 |
10 |
||
5 |
|
|
|
|
|
∞ |
∞ |
∞ |
3 |
∞ |
∞ |
|
6 |
|
|
|
|
|
∞ |
∞ |
∞ |
∞ |
1 |
∞ |
|
|
D(4) |
|
1 |
2 |
3 |
4 |
5 |
6 |
||||
|
|
|||||||||||
1 |
|
|
|
|
|
5 |
1 |
4 |
3 |
7 |
5 |
|
2 |
|
|
|
|
|
4 |
5 |
3 |
2 |
6 |
4 |
|
3 |
|
|
|
|
|
∞ |
∞ |
∞ |
∞ |
∞ |
1 |
|
4 |
|
|
|
|
|
2 |
3 |
1 |
5 |
4 |
2 |
|
5 |
|
|
|
|
|
5 |
6 |
4 |
3 |
7 |
5 |
|
6 |
|
|
|
|
|
∞ |
∞ |
∞ |
∞ |
1 |
∞ |
|
D(6) |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
||||
|
||||||||||||
1 |
|
|
|
|
5 |
1 |
4 |
3 |
6 |
5 |
||
2 |
|
|
|
|
4 |
5 |
3 |
2 |
5 |
4 |
||
3 |
|
|
|
|
7 |
8 |
6 |
5 |
2 |
1 |
||
4 |
|
|
|
|
2 |
3 |
1 |
5 |
3 |
2 |
||
5 |
|
|
|
|
5 |
6 |
4 |
3 |
6 |
5 |
||
6 |
|
|
|
|
6 |
7 |
5 |
4 |
1 |
6 |
||
55

С задачей определения кратчайших путей в графе тесно связана задача транзитивного замыкания бинарного отношения. Под бинарным отношением на множестве V мы понимаем произвольное подмножество E V×V. Такое отношение является транзитивным, если выполняется условие: если <x,y> E и <y,z> E, то <x,z> E для произвольных x,y,z V. Бинарное отношение E V×V можно однозначно представить ориентированным графом G=<V,E>. Для такого отношения определим
E*={<x,y>: в G=<V,E> существует путь ненулевой длины из x
в y}.
E*- транзитивное отношение на множестве V и E E*. Отношение E* называется транзитивным замыканием.
Если отношение E представить в виде графа G=<V,E>, то транзитивное замыкание E* можно вычислить по алгоритму УоршаллаФлойда. После завершения работы алгоритма имеем:
<vi,vj> E* D[i,j]<∞
При вычислении транзитивного замыкания удобно принять
W[i,j] = 1, если < vi ,v j > E,
0, если < vi ,v j > E ( вместо ∞).
Процедура вычисления транзитивного замыкания, основанная на алгоритме Уоршалла-Флойда, имеет следующий вид.
begin
for i=1 to n do
for j=1 to n do D[i,j]=W[i,j]; for m:=1 to n do
for i:=1 to n do for j:=1 to n do
D[ i, j ] := D[ i, j ] ( D[ i,m ] D[ m, j ])
end
Здесь и - булевы операции.
После завершения работы алгоритма имеем:
|
< vi ,v j > E |
* |
, |
||
1, если |
|
||||
D[i,j] = |
< v ,v |
|
> E* . |
||
0, если |
j |
||||
|
i |
|
|
|
|
Матрица D[ i, j ]i , j=1,n |
называется матрицей связности (дости- |
||||
жимости) графа G=<V,E>.
56

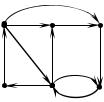
Пример 14.2. Определить матрицу связности графа
|
|
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
||||||
1 |
2 |
|
1 |
0 |
1 |
0 |
0 |
0 |
|
2 |
0 |
0 |
1 |
0 |
0 |
||||
|
W = |
||||||||
|
3 |
3 |
0 |
0 |
0 |
1 |
0 |
||
5 |
4 |
4 |
0 |
1 |
0 |
0 |
0 |
||
|
|
5 |
1 |
0 |
0 |
1 |
0 |
||
D(1) |
|
1 |
2 |
3 |
4 |
5 |
|
|
D(2) |
|
|
1 |
2 |
3 |
4 |
5 |
|
||
|
|
|
|
|
|||||||||||||||
1 |
|
0 |
1 |
0 |
0 |
0 |
1 |
|
|
|
0 |
1 |
1 |
0 |
0 |
|
|||
2 |
|
0 |
0 |
1 |
0 |
0 |
2 |
|
|
|
0 |
0 |
1 |
0 |
0 |
|
|||
3 |
|
0 |
0 |
0 |
1 |
0 |
3 |
|
|
|
0 |
0 |
0 |
1 |
0 |
|
|||
4 |
|
0 |
1 |
0 |
0 |
0 |
4 |
|
|
|
0 |
1 |
1 |
0 |
0 |
|
|||
5 |
|
1 |
1 |
0 |
1 |
0 |
5 |
|
|
|
1 |
1 |
1 |
1 |
0 |
|
|||
D(3) |
|
|
1 |
2 |
3 |
4 |
5 |
|
|
D(4) |
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|||||||||||||
1 |
|
|
0 |
1 |
1 |
1 |
0 |
1 |
|
|
0 |
1 |
1 |
1 |
0 |
|
|||
2 |
|
|
0 |
0 |
1 |
1 |
0 |
2 |
|
|
0 |
1 |
1 |
1 |
0 |
|
|||
3 |
|
|
0 |
0 |
0 |
1 |
0 |
3 |
|
|
0 |
1 |
1 |
1 |
0 |
|
|||
4 |
|
|
0 |
1 |
1 |
1 |
0 |
4 |
|
|
0 |
1 |
1 |
1 |
0 |
|
|||
5 |
|
|
1 |
1 |
1 |
1 |
0 |
5 |
|
|
1 |
1 |
1 |
1 |
0 |
|
|||
D(5) |
|
1 |
2 |
3 |
4 |
5 |
|
Тогда граф G*=<V,E*> будет |
|
|
|
||||||||
|
|
|
|
|
|
|
|
иметь вид |
|
1 |
|
0 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
||||||
2 |
|
0 |
1 |
1 |
1 |
0 |
(4) |
|
2 |
3 |
|
0 |
1 |
1 |
1 |
0 |
=D |
1 |
3 |
4 |
|
0 |
1 |
1 |
1 |
0 |
|
|
|
5 |
|
1 |
1 |
1 |
1 |
0 |
|
5 |
4 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
57 |
ЛИТЕРАТУРА
1.Иванов Б.Н. «Дискретная математика. Алгоритмы и программы». // М.: Изд-во «Лаборатория базовых знаний», 2003.
2.Харари Ф. «Теория графов». // М.: "Мир", 2007.
3.Ю.В. Гайдамака, К.Е. Самуйлов, Л.А. Севастьянов, С.С. Спесивов «Комбинаторика. Алгоритмы на графах». Учеб- но-методическое пособие. // М.: Изд-во РУДН, 2002.
4.Г.П. Гаврилов, А.А. Сапоженко «Сборник задач по дискретной математике». // М.: Наука, 2007.
58
