Лекции_1_курс

Задача.

Пароход двигается равномерно по течению реки и проходит путь относительно берега S за время t1 , а против течения тот же путь за время t2 . Определить скорость течения реки (Vр ) и скорость парохода относительно воды (Vп ).

Решение.

Уравнения описывающие движение парохода по течению реки и против ее течения имеют вид:

(Vп +Vр ) t1 = S ,

(Vп −Vр ) t2 = S .

Из этих уравнений следует:

Аналогично скоростям, различают абсолютное ( aабс), относительное ( arотн ) и переносное ( aпер) ускорения.

Абсолютное ускорение полностью определяется отношением геометрического приращения абсолютной скорости (

dVабс ) к промежутку времени, за которое оно происходит ( dt ),

т.е. arабс = dVdtабс . Однако, при этом, ускорение тела относительно

условно неподвижной системы отсчета ( aабс) определяется не только суммой ускорений подвижной системой отсчета ( arпер) и

значением ускорения тела относительно нее ( aотн ), но и

11

«поворотным» ускорением ( aпов), зависящем от угловой скорости

вращения подвижнойr системы отсчета (ω) и скорости движения

тела в ней (Vотн).

aабс = aпер + aотн + aпов

Расчет показывает, что

arпов = 2 [ωr ×Vотн ],

или в скалярной форме

aпов = 2 ω Vотн sinα

где α - угол между векторами ω и Vотн.

Это ускорение Кориолиса.

2. Основы динамики.

В предыдущих разделах изучалось движение тел (материальной точки), вне зависимости от причин вызывающих его. Динамика, это раздел механики, в котором изучаются характеристики движения тел в зависимости от сил, действующих на эти тела.

2.1.Инерциальные системы отсчета. Первый закон Ньютона

Рассмотрим тело, находящееся столько далеко от других тел, что оно не испытывает их воздействие. Такое тело называется свободно движущимся. Конечно, в природе таких тел нет, однако предположить это, в рамках классической физики, мы можем.

Свободное движение, как и всякое другое, выглядит поразному в различных системах отсчета. Однако, если выбрать в качестве тела отсчета другое свободно движущееся тело, то относительно него свободное движение других тел будет

12

выглядеть наиболее просто - движение будет прямолинейным и равномерным.

Система отсчета, связанная со свободно движущимся телом, называется инерциальной системой отсчета.

Свободное движение тел в инерциальной системе отсчета всегда прямолинейно и равномерно.

Этот закон инерции был впервые сформулирован Галилеем

(1632г.). Закон инерции также называется первым законом

Ньютона.

Все физические явления, за редким исключением, изучают в инерциальных системах, которые, фактически, являются таковыми только приблизительно. Система отсчета связанная с Землей не является инерциальной, о чем свидетельствует изменения плоскости колебаний маятника с течением времени (маятник Фуко).

2.2.Масса. Количество движения. Сила. Второй закон Ньютона. Третий закон Ньютона

В1687 году Ньютон опубликовал свой фундаментальный труд «Математические начала натуральной философии», в котором впервые отчетливо было введено понятие «масса» и указано на то, что масса и вес существенно разные физические характеристики.

Всоответствии с представлениями Ньютона, под массой

(m)будем понимать величину, характеризующую:

-количество материи в теле,

-меру инертности тела и

-являющуюся объектом и источником тяготения.

Масса измеряется в граммах (система СГС) или в килограммах (интернациональная система, СИ). Эталон единицы массы хранится в палате мер и весов в Париже.

Количеством движения в физике называют векторную величину, равную произведению массы тела на скорость его движения:

P = m V

Если тело совершает свободное движение, то его количество движения не меняется. Если же на тело оказывают

13

действие другие тела, то его величина меняется и поэтому изменение количества движения можно рассматривать как меру воздействия на данное тело других тел.

Предположим, что в момент времени t тело имело количество движения P , а в момент времени t + dt , его величина стала Pr + dPr. Изменение количества движения за промежуток

времени dt составляет dP . Величина ddtP характеризует скорость

изменения количества движения и называется силой ( F ).

Изменение количества движения пропорционально приложенной движущей силе и происходит в направлении действия этой силы.

Fr = ddtP .

Это равенство называется уравнением движения и является отображением второго закона Ньютона.

Если масса тела величина постоянная, то

Fr = dmdtV = m ddtV = mar.

Если известно поле действия сил, зависимость F(x, y, z),

координаты положения и скорость тела в некоторый момент времени, то уравнение движения позволяет вычислить координаты, скорость и ускорение материальной точки в любой момент времени. Компоненты вектора силы в Декартовой системе координат определяют характер движения материальной точки по соответствующим направлениям:

r

Frx = ddtPx = marx , Fry = ddtPy = mary , Frz = ddtPz = marz

Третий закон Ньютона устанавливает характер взаимодействия между телами, действующими друг на друга:

14

действия двух тел друг на друга всегда равны и противоположно направлены.

Пример: с какой силой тело действует на подставку, с такой же силой, но противоположно направленной, подставка действует на тело.

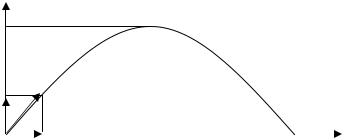
Задача.

Тело брошено в поле тяжести Земли с начальной скоростью V0 под углом α к горизонту. Определить

максимальную высоту подъема тела и дальность его полета.

Для решения этой задачи выберем в качестве тела отсчета Землю, а систему координат расположим таким образом, что движение будет происходить в плоскости x, y из точки с

x0 = y0 = 0

x

hmax

В выбранной системе отсчета, компоненты начальной скорости в направлениях x и y имеют вид

V0 x =V0 sin(α), V0 у =V0 cos(α)

Так как вдоль оси y на тело не действует сила, движение вдоль нее будет равномерным и происходить со скоростью V0 y ,

15

при этом положение тела на этой оси будет определяться выражением y =V0 yt . При этом, дальность полета тела ( ymax )

зависит от времени полета ( tt ):

ymax =V0tt cosα .

Движение тела вдоль оси x осложнено действием силы тяжести, направленной в сторону, противоположную направлению начальной скорости V0x . Предполагая, что ускорение свободного

падения ( g ) не зависит от высоты подъема тела, из уравнения Vx =Vox − gt с учетом того, что в точке максимального подъема Vx = 0 определим время подъема ( tп )

Основываясь на том, что время подъема и время падения тела равны, а при данной постановке задачи это так и есть (диссипативные силы отсутствуют), находим, что время полета тела равно:

tt = 2tп = 2V0 sin(α). g

Следовательно, максимальная дальность полета тела определяется выражением:

Из полученного выражения видно, что при угле α = π4

дальность полета тела будет максимальной из возможных для

16

данной начальной его скорости и что дальность полета тела одинакова при углах π6 и π3 .

2.3. Вращательное движение твердого тела.

Движение твердого тела может быть поступательным и вращательным. При поступательном движении твердого тела все его элементарные объемы имеют одинаковую скорость и описывают в пространстве одинаковые траектории, смещенные друг относительно друга.

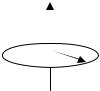
При вращательном движении вокруг некоторой оси элементарные объемы твердого тела описывают окружности в плоскостях, перпендикулярных оси вращения. Каждый элементарный объем движется со скоростью

V = [ωr ×rr]

где V - скорость движения элементарного объема вдоль

dϕ -угол поворота тела за время dt , r - кратчайшее расстояние

от оси вращения до рассматриваемого элементарного объема тела

(см. рис. 2.2).

ω

V

r

Рис. 2.2.

Угловая скорость - векторная величина. Направление угловой скорости определяется правилом буравчика.

17

2.4. Момент инерции

Определим кинетическую энергию тела, совершающего вращательное движение. Для поступательного движения дело обстоит просто: т.к. все точки тела движутся с одинаковой

скоростью (V ), то кинетическая энергия будет определяться выражением Eкин = MV2 2 , где M масса всего тела.

Определим теперь кинетическую энергию вращательного движения. Для этого, мысленно разделим тело на элементарные

объемы и будем считать их материальными точками. Если mi масса i -го элемента, а ri - кратчайшее расстояние этого элемента до оси вращения, то модуль его скорости будет равна Vi = ω ri ,

где ω - угловая скорость вращения тела. Кинетическая энергия этого элемента тела будет равна

Ei = mi2Vi2 = 12 ω2 mi ri2 .

Очевидно, полная кинетическая энергия вращения твердого тела определяется суммой кинетических энергий всех составляющих тело элементов, т.е.

где I = ∑mi ri2 и зависит только от распределения массы тела

i

относительно оси предполагаемого вращения. Эта величина называется моментом инерции. Как мы увидим в дальнейшем,

момент инерции характеризует инерционные свойства тела способного вращаться и является аналогом массы при вращательном движении.

В общем случае, момент инерции находится интегрированием:

19

r2

I = ∫r 2 dm

r1

Пределы интегрирования определяются распределением массы тела относительно оси предполагаемого вращения, зависимостью m от r .

Рассмотрим некоторые частные случаи.

1. Вычислим момент инерции однородного длинного тонкого стержня (длина стержня l, его масса M ), ось предполагаемого вращения которого перпендикулярна его оси симметрии и проходит через его центр инерции.

Рис. 2.4.

Очевидно, масса стержня M = ρ ϑ = ρπa2 l, где ρ -

плотность материала тела, ϑ - объем тела, a - радиус стержня. Единственной переменной величиной зависящей от расстояния до оси вращения является длина, поэтому выражение для dm имеет

вид: dm = ρπa2 dr , где r - та переменная, по которой

производится интегрирование. Пределы интегрирования определяются положением оси предполагаемого вращения. В