Криптоанализ алгоритма Rijndael. Перевод А. Гончарова

_______________________________________________________________________________________________

Криптоанализ алгоритма Rijndael.

Niels Ferguson, John Kelsey, Stefan Lucks, Bruce Schneier, Mike Stay, David Wagner, and Doug Whiting.

Перевод Алексея Гончарова.

Москва, 2000

Криптоанализ алгоритма Rijndael.

1. Введение.

Rijndael - один из пяти шифров, прошедших во второй раунд конкурса на получение статуса AES. В своей структуре он имеет 10, 12, или 14 тактов криптопреобразования в зависимости от длины ключа. Ранее был известен метод, позволяющий взломать до 6-ти тактов алгоритма. В этой работе описывается атака на 7-ой такт Rijndael.

В разделе 2 описывается техника "частичных сумм", которая позволяет очень сильно снизить сложность осуществления шеститактовой атаки. Также показывается, как применить эту идею для атак на 7-ой и 8-ой такты криптопреобразования, используя дополнительные открытые тексты (если это возможно), чтобы снизить сложность атаки. Атаки на семитактовый Rijndael со 128-битным ключом и на восьмитактовый со 192-битным и 256-битным ключом требуют почти полный набор шифров (2¹²⁸-2¹¹⁹ известных открытых текстов); поэтому они не имеют практического применения вследствие недоступности необходимых вычислительных мощностей. Все эти атаки используют расширение специализированной Square - атаки, названной по имени алгоритма Square (предтечи Rijndael), для которого она разрабатывалась.

В разделе 3 рассматривается задача генерации ключей (ключеформирования); показываются отдельные необычные свойства ключеформирования, которые можно рассматривать как нарушение общепризнанных критериев построения шифра. Несмотря на то, что пока не известно каких - либо атак, которые основывались бы на этих свойствах, наличие этих качеств настораживает.

В заключение, в разделе 4 используется слабая диффузия ключеформирования в Rijndael для разработки зависящей о ключа атаки, которая может быть применена к девятитактовому Rijndael с 256-битным ключом.

Итоги этих атак, включающие величины временной и информационной сложностей, приведены в таблице 1. Так же рекомендуется просмотреть приложение А для ознакомления с обозначениями, используемыми в описании этапов криптопреобразования.

Шифр	Длина ключа	Сложность		Комментарии
		Данные	Время
Rijndael-6	любая	232 CP	272	известная ранее атака
Rijndael-6	любая	6*232 CP	244	частичные суммы
Rijndael-7	192	19*232 CP	2155	частичные суммы
Rijndael-7	256	21*232 CP	2172	частичные суммы
Rijndael-7	любая	2128-2119 CP	2120	частичные суммы
Rijndael-8	192	2128-2119 CP	2188	частичные суммы
Rijndael-8	256	2128-2119 CP	2204	частичные суммы
Rijndael-9	256	285 RK-CP	2224	атака, зависящая от ключа

CP - открытые тексты (Chosen Plaintext),

RK-CP - открытые тексты, зависящие от ключа.

Таблица 1. Результаты атак на Rijndael.

2. Square-атака.

1. Известная 6-тактовая атака.

Техника, рассматриваемая далее, впервые была задействована при разработке атаки на блочный шифр Square; она применима ко всем блочным шифрам с любой длиной ключа.

Обозначим через m^(r), b^(r) и t^(r) значения текста, используемые в такте r после операций перемешивания столбцов (MixColumn), добавления ключа (key addition) и сдвига строк (ShiftRow) соответственно. Обозначим через k^(r) тактовый ключ цикла r, через k^(r)' - эквивалентное значение тактового ключа, которое может быть XORено с данными перед операцией перемешивания столбцов, а не после. При необходимости посмотрите в приложении А более подробное объяснение используемых обозначений.

Атака начинается с получения 256-ти криптограмм, различающихся только в одном байте m⁽¹⁾, которые охватывают все возможные значения данного байта. Один байт m⁽¹⁾ зависит от 4-х байтов открытого текста и от 4-х байтов ключа k⁽⁰⁾. Для этого выберем 2³² открытых текстов, с фиксированной общей частью и варьирующейся частью размером в 4 байта, охватывающей все возможные 2³² значений. Затем задаемся произвольными значениями 4-х байтов ключа. Для каждого возможного значения байтов ключа можно найти 2²⁴ групп по 256 открытых текстов, которые, будучи подвергнуты операции перемешивания столбцов, внутри своей группы будут отличаться только одним байтом из m⁽¹⁾; так как открытые тексты были различны, то этот байт из m⁽¹⁾ примет все 256 возможных значений.

Отслеживая изменения внутри шифра, заметим, что каждый из байтов t⁽⁴⁾ примет все возможные значения. Если мы просуммируем значения каждого из этих байтов по всем 256 криптограммам, то получим ноль. Это свойство характерно для линейной функции, поэтому каждый из байтов из m⁽⁴⁾ и из b⁽⁴⁾ также дадут ноль при суммировании их значений во всех 256-ти криптограммах.

Теперь посмотрим, как байт из b⁽⁴⁾ связан с байтами из криптограммы. Для анализа мы незначительно изменили структуру шифра и поместим добавление ключа перед преремешиванием столбцов в такте 5. Вместо перемешивания столбцов и добавления ключа k⁽⁵⁾ мы вначале добавим ключ k^(5)', а потом применим перемешивание столбцов. При такой конфигурации легче разглядеть, что любой байт из b⁽⁴⁾ зависят от шифртекста, 4-х байтов ключа k⁽⁶⁾ и одного байта псевдоключа k^(5)'. Мы предположим значения этих 5-ти байт ключа, вычислим значение байта из b⁽⁴⁾ для всех 256 криптограмм и найдем ту, для которой сумма соответствующих байт равна нулю.

Для каждой группы из 256 криптограмм такая фильтрация забракует 256 из 256-ти для всех неверных предположений о значении ключа. Если бы проверялись значения для всех 9-ти байтов ключа, то потребовалось бы 10 или более групп из 256 криптограмм, чтобы найти весь ключ.

В качестве обобщения заметим, что эта атака требует 2³² выбранных открытых текстов, 2³² ячеек памяти для хранения пар текст/шифрограмма, и 2⁷² шагов для выяснения 9-ти байтов ключа. Каждый шаг включает в себя частичную дешифрацию 256 криптограмм, но правильное упорядочивание вычислений может сделать это очень быстрым. Это сравнимо по времени с одиночным шифрованием. Общая вычислительная сложность этой атаки порядка 2⁷² шифрований.

2. Расширение до 7-ми тактов.

Предыдущая атака может быть распространена на 7-тактовый шифр со 192-битным и 256-битным ключом. Достаточно угадать 16 байт последнего тактового ключа. Если действовать прямо, то это добавляет 128 бит к угадыванию ключа, а временные затраты возрастают до 2²⁰⁰; требования к открытым текстам и памяти не изменяются, несмотря на то, что необходимо использовать больше групп для проверки потенциальных ключей.

Эта процедура может быть усовершенствована. Ключеформирование обеспечивает зависимость между байтами расширенного ключа, и это можно использовать для атаки. Для 192-битного ключа угадывание последнего тактового ключа k⁽⁷⁾ дает 2 из 4-х байтов k^(6)', который должен быть отгадан, плюс байт из k^(5)', который также нужно отгадать. Это уменьшает размер угадываемого ключа на 24 бита, что дает общую сложность порядка 2¹⁷⁶. Для 256-битного ключа байты при ключеформировании выровнены другим образом. Угадывание всего k⁽⁷⁾ не дает никакой информации о k^(6)', но дает один байт из k^(5)'. Для этой длины ключа сложность атаки равна 2¹⁹².

3. Усовершенствование.

Атака на 6-тактовый Rijndael, описанная в разделе 2.1, может быть улучшена. Вместо угадывания 4-х байтов k⁽⁰⁾ мы просто задействуем все 2³² открытых текста. Для любого значения первого тактового ключа эти криптограммы содержат 2²⁴ групп по 2⁸ криптограмм, различающихся только в одном байте m⁽¹⁾. Все, что будет делаться далее, аналогично предыдущей атаке: угадываем 5 байт ключа в конце шифра, частично дешифруем один байт b⁽⁴⁾, суммируем его значение со всеми остальными в криптограммах и проверяем на нулевой результат. По сравнению с первоначальной версией, мы узнаем только 40 бит ключа вместо 72. Но с другой стороны, мы должны затратить только 2²⁴ операций для каждого угадывания. Это усовершенствование уменьшает затраты на 2⁸, но требует около 6*2³² открытых текстов для обеспечения достаточного числа наборов, необходимых для однозначной идентификации истинного значения 5-ти байт ключа.

Рассмотрим эту атаку более детально. Получив 2³² криптограмм, мы угадываем 5 байт ключа, частично дешифруем один байт b⁽⁴⁾ из всех криптограмм и суммируем эти байты по всем криптограммам. Рассмотрим эту частичную дешифрацию. В любом шифртексте мы используем только 4 байта. Каждый из них XORится c байтом ключа, затем к каждому байту применяется обратный S-box, и в завершении умножается на заданную часть инверсной MSD-матрицы. Четыре байта XORятся вместе, 5-ый байт ключа XORится с результатом применения обратного S-box`а, и полученные значения суммируются по всем шифртекстам.

Обозначим через c_i,j j-ый байт i-ой криптограммы. Для простоты поставим в соответствие байтам, используемым нами в каждом блоке шифртекста, номера от 0 до 3. Пусть k₀,…,k₄ соответствуют 5-ти байтам ключа, которые пытаемся отгадать. Мы хотим вычислить

(1),

где S₀,…,S₃ - биективные S-box`ы, каждый из которых содержит инверсный Rijndael-S-box и следующее за ним умножение на инверсную MDS-матрицу. Имея 2³² криптограмм и 2⁴⁰ возможных значений ключа, мы получим для суммирования 2⁷² различных значений, которое в грубой оценке требует затрат порядка 2⁶⁴ стандартных операций шифрования.

Мы можем организовать эту работу более производительно следующим образом: для каждого k мы поставим в соответствие каждой криптограмме c "частичную сумму" x_k, определяемую следующим образом:

.

Это даст нам отображение (с₀, с₁, с₂, с₃) (x_k, c_k+1,…,c₃), которое можно применить к каждому из шифртекстов, если мы знаем k₀,…,k_k.

Мы начинаем со списка из 2³² криптограмм, угадываем k₀ и k₁ и вычисляем, как часто каждая триада (x₁, c₂, c₃) попадает в список. C этой целью для каждого i вычислим 3-байтовое значение как функцию от шифртекста и угадываемого ключа, и подсчитаем, сколько раз каждое 3-байтовое значение появляется в процессе этих вычислений. Возможно появление 2²⁴ различных 3-байтовых значений, но нам не нужно хранить список всех значений; нам нужно только число появлений каждой триады. Мы угадаем k₂ и вычислим, как часто встречается пара (x₂, c₃); угадаем k₃ и вычислим, как часто встречается значение x₃. Наконец, мы угадаем k₄ и вычислим долгожданную сумму.

Так как все суммы берутся с использованием XOR, и так как для любыхz, то этого достаточно только для подсчетов по модулю 2. Таким образом, для каждого счетчика достаточно одного бита, и для всех 2²⁴ счетчиков требуется 2²⁴ бит.

Как много времени на это затратится? На первом этапе мы угадываем 16 бит и обрабатываем 2³² криптограмм, что в сумме дает 2⁴⁸ операций. На следующем этапе мы угадываем еще 24 бита, но при этом обрабатываем только 2²⁴ триад, что в сумме дает 2⁴⁸ операций. В итоге, мы получаем 2⁴⁸ вычислений выражения (1), или порядка 2⁵⁰ вычислений S-box.

Это итоговая работа, неоходимая при единичной структуре из 2³² криптограмм. Первая структура уже очищена от подавляющего большинства неверных ключей, но мы все еще должны пройти первые шаги вычисления частичных сумм для каждой из шести структур, которые нами используются. Таким образом, общее число S-box`ов возрастает до 2⁵².

Используя приближенное равенство 2⁸ S-box'ов одному стандартному криптопреобразованию, получим, что 2⁵² S-box'ов сравнимы с 2⁴⁴ операций. Это значительное достижение по сравнению с предыдущим объемом работ 2⁷².

3. Расширение до 7-ми тактов.

Мы можем применить усовершенствование к 7-тактовой атаке из раздела 2.2. Для выражения байта из b⁽⁴⁾ через ключ и шифртекст мы возьмем формулу, подобную (1), но трехуровневую, 16 байт криптограммы и 21 байт ключа. Техника "частичных сумм" поможет только во время последней части вычислений, потому что она сэкономит время, если мы имеем больше криптограмм, чем возможных значений промежуточного результата. При наличии в структуре 2³² пар текст/шифрограмма эта техника не поможет нигде за исключением последнего шага вычислений.

Для схемы со 192-битным ключом мы может сначала угадать 128 бит последнего тактового ключа. Эти биты будут также определять 2 из 4-х байт 6-го такта, и один байт ключа 5-го такта. Таким образом, после угадывания последнего тактового ключа мы можем уменьшить каждую структуру до 2²⁴ счетчиков с помощью техники "частичных сумм". Используя некоторые предварительно вычисленные таблицы, мы можем сделать это для каждой из 2¹²⁸ догадок примерно за 2³² обращений к памяти. Следующая стадия приносит еще один байт и требует 2²⁴ шагов для уменьшения частичных сумм до 2¹⁶ счетчиков, и последний этап дает последний оставшийся байт и получает конечный результат. Каждая из этих фаз занимает около 2¹⁶⁰ шагов. Мы имеем три этапа, каждый из которых требует 2¹⁶⁰ шагов, и нам нужно обработать три структуры, прежде чем начать выделение догадок для последнего тактового ключа, поэтому общие затраты на эту атаку составляют порядка 2¹⁶³ S-box'ов или около 2¹⁵⁵ обычных криптопреобразований.

Для 256-битного ключа выравнивание в процессе ключеформирования различное. Получение последнего тактового ключа не дает нам никакой информации о ключе 6-го раунда, но говорит немного больше о ключе 5-го такта. Работая с простой структурой как раньше, мы получим 128 бит последнего тактового ключа и вычислим 4 байта ключа 6-го такта для каждого из 2³² текстов за общее время порядка 2¹⁶⁰. На следующем этапе мы получим еще 16 бит ключа и результаты в 2²⁴ однобитовых счетчиках за общее время порядка 2¹⁷⁶. Дальнейшие фазы расчитываются аналогичным способом. Затраты времени на структуру составляют приблизительно 2¹⁷⁸ S-box'ов или 2¹⁷⁰ криптопреобразований. Необходимо пять структур, прежде чем начать отбрасывание догадок о последнем тактовом ключе, поэтому общая сложность этой атаки составляет примерно 2¹⁷².

3. Второе усовершенствование.

Возможно дальнейшее преобразование технологии атаки при условии, что считается целесообразным уменьшить временную сложность за счет увеличения информационных затрат.

Вначале будет показано, что 7-тактовый Rijndael может быть сломан при наличии 2¹²⁸ известных текстов при временных затратах порядка 2¹²⁰ обычных шифрований. Эти шифрования разделяются на 2⁹⁶ пакетов по 2³² шифрований в каждом, различающиеся только в четырех байтах m⁽¹⁾. Эти 4 байта находятся на местах, необходимых для применения атаки из раздела 2.3: конкретно каждый пакет из 2³² шифрований содержит 2²⁴ групп по 2⁸ шифрований, которые различаются только одним байтом m⁽²⁾. Соответственно, мы можем рассматривать содержимое набора из 2¹²⁸ шифрований как 2¹²⁰ групп по 2⁸ шифрований, которые отличаются только в одном байте m⁽²⁾. Это обеспечивает, что суммирование одного байта из b⁽⁵⁾ по всем 2⁸ криптограммам в группе даст ноль, и суммирование по всем 2¹²⁸ криптограммам также даст ноль. На этом простом свойстве и базируется атака, описываемая ниже.

Самый простой путь использования этого свойства- это угадать 5 байт ключа в конце шифра, частично расшифровать один байт b⁽⁵⁾ каждого блока шифртекста, просуммировать по всем 2¹²⁸ криптограммам и проверить на ноль. Однако этот простой путь непригоден. Любой неправильный ключ даст ноль после суммирования байта из b⁽⁵⁾ по всем 2¹²⁸ криптограммам, потому что для любого биективого 128-битного блочного шифра b⁽⁵⁾ (или любая другая промежуточная величина) принимает все возможные 128-битовые значения в течение своего цикла из 2¹²⁸ криптопреобразований. Следовательно, необходимо слегка модифицировать атаку.

Будем использовать следущую технику: сфокусируем внимание на 5-ом байте m⁽¹⁾ (отличного от 4 байт, выбранных ранее), скажем, m_a,b⁽¹⁾. Зафиксируем значение x для этого байта, дающее нам 2¹²⁰ криптограмм, где m_a,b⁽¹⁾ = x; это даст нам список из 2⁸⁸ пакетов, каждый из которых содержит 2²⁴ групп по 2⁸ шифрограмм, которые различаются только в одном байте m⁽²⁾. Назовем эту структуру из 2¹²⁰ шифрограмм "кучей". Теперь мы получим 2¹²⁸ известных текстов (2⁸ куч), угадаем 4 байта ключа начала шифра, вычислим m_a,b⁽¹⁾ для каждого шифртекста, используя угаданный ключ, и разделим тексты на кучи. Проверим одну из куч, не дает ли байт из b⁽⁵⁾ при суммировании по всем криптограммам кучи ноль; получение нуля маловероятно при неверном предположении значения ключа. Этому работающему варианту атаки подвержен 7-тактовый Rijndael, но сложность его очень велика (2¹²⁸ x 2⁷² шагов вычислений и более).

Только одно может улучшить положение. Заметим, что байт из b⁽⁵⁾ зависит только от 4-х байтов шифртекста (для простоты назовем их c₀,…,c₃), а байт m_a,b⁽¹⁾ зависит только от 4-х байтов открытого текста (скажем, p₄,…,p₇). Используем трехфазовую атаку: на первом этапе используем 2⁶⁴ счетчиков m_y, на втором - 2³² счетчиков n_z, а на третьем - проведем фильтрацию информации по вариантам ключа. Как обычно, все счетчики могут суммировать по модулю 2, поэтому каждому счетчику необходим только один бит памяти.

Атака протекает так, как описано далее. На первом этапе, мы увеличиваем значения счетчика m_y в соответствии со значением 64-битного параметра y = (c₀,…,c₃,p₄,…,p₇), которое мы вычисляем для каждой пары текст/криптограмма. На втором этапе угадываем 4 байта ключа первого цикла, разделяем счетчики на кучи (вычисляя m_a,b⁽¹⁾ для каждого состояния счетчика используя (p₄,…,p₇) и угаданную часть ключа), выбираем одну кучу и обновляем счетчик n_z, прибавляя к нему m_y, для всех y из этой кучи, в соответствии с z = (c₀,…,c₃). Далее, на третьем этапе, мы угадываем 5 байт ключа конца шифра, частично расшифровываем каждый z в один байт b⁽⁵⁾, суммируем эти байты по всем 2³² значениям z (с разделением по n_z), и проверяем на нулевой результат. Третий этап должен быть повторен для каждого значения 4 байт ключа начала шифра.

Какова сложность этой атаки? Превый этап предусматривает изменение счетчиков для каждого блока шифртекста, что является эквивалентом 2⁸ ячеек памяти для обычного криптопреобразования; подсчет займет время, сравнимое с 2¹²⁰ обычных шифрований. В сравнении с первым этапом мощности, затрачиваемые на остальную часть атаки пренебрежимо малы (порядка 2⁹⁶ шифрований); здесь не требуется вычисление частичных сумм.

Было показано, что можно взломать 7-тактовый Rijndael, используя 2¹²⁸ известных текстов, время, эквивалентное 2¹²⁰ шифрований и 2⁶⁴ бит памяти. Эта 7-тактовая атака использует большое число известных текстов, но при этом имеет меньшую временную сложность; ее общая сложность эквивалентна сложности атаки из раздела 2.3, но в отличие от нее, применима к ключам любой длины (включая 128-битовые).

Еще одно крошечное усовершенствование. Мы используем один байт из m⁽¹⁾ для разделения на кучи, а так же 4 байта открытого текста и угаданные 4 байта ключа первого такта для определения 4-х байтов m⁽¹⁾. Мы могли бы сделать больше куч с меньшими размерами, зафиксировав 3 байта m⁽¹⁾ для каждой кучи. Это даст нам 2²⁴ куч по 2¹⁰⁴ текстов каждая. Точно также мы можем определиться, какие из 4-х байт будут связаны с разделением на кучи, что даст нам 2²⁶ куч по 2¹⁰⁴ текстов каждая, причем каждый текст будет использоваться в 4-х разных кучах. Более того, нам не нужны все пары текст/криптограмма. Если 4 байта открытого текста дают 2³² - 2²³ значений из 2³² возможных (и для каждого из этих значений оставшиеся 12 байт принимают все возможные значения), поэтому около половины куч содержит неверные пары текст/шифртекст, тогда как другая половида полна и неповреждена. Нам хотелось бы использовать неповрежденные кучи в нашей атаке. Это снизит требования до 2¹²⁸ - 2¹¹⁹ текстов. Эти изменения не затрагивают вычисления сложности атаки, но дают небольшое снижение требований к текстам.

3. Расширение до 8-ми тактов.

Хотелось бы распространить идею атаки на и 8-ой такт Rijndael, но только не на 128-битный ключ. Как и прежде, получив 2¹²⁸ - 2¹¹⁹ текстов (около 2²³ неповрежденных куч), сфокусируем внимание на на одной куче, используя тот факт, что один байт из b⁽⁵⁾ дает ноль при суммировании по всем 2¹⁰⁴ шифрограммам из кучи. Однако, байт из b⁽⁵⁾ зависит теперь от шифртекста и от 21 байта подключа конца шифра, поэтому теперь мы можем применить технику "частичных сумм" из раздела 2.4. Угадав 4 байта ключа первого такта, определим кучи и вычислим частичные суммы x_k, затратив на это 2¹⁰⁴ бит памяти и время, эквивалентное 2²⁰³ шифрований. Общая сложность атаки составляет около 2²⁰⁴ шифрований, что быстрее, чем полный поиск 256-битного ключа перебором.

Так как эта атака требует более чем 2²⁰⁴ шифрований, то ее бессмысленно использовать для 192-битных ключей. Но 192-битное ключеформирование допускает ускорение 8-тактовой атаки, которая следовательно требует около 2^204-16=2¹⁸⁸ шифрований. Важно, что временная сложность равна 2¹⁸⁸ шифрований только для 192-битных ключей, а не для 256-битных.

Каждый байт b⁽⁵⁾ зависит от 21 байта подключей, а конкретно: от всех 16 байт k⁽⁸⁾, 4 байт k^(7)', и от одного байта k^(6)'. Аналогично разделу 2.2, зафиксируем последний тактовый ключ k⁽⁸⁾, определяющий два из четырех байтов k^(7)' и возможно, в зависимости от того, какой байт из b⁽⁵⁾ нам нужен, определим так же нужный байт из k^(6)'. Точнее, выбрав 3 столбца (12 байт) из k⁽⁸⁾, мы можем определить 2 столбца из k^(7)', а выбрав 4 столбца из k⁽⁸⁾ - один столбец из k^(6)'. В каждом столбце из k^(7)' находится один байт подключа, необходимый для атаки. Другими словами, зафиксировав k^(8)' (или только три столбца из k^(8)'), мы получим два необходимых для атаки байта из k^(7)'. Таково свойство 192-битного ключеформирования.

Для описания атаки рассмотрим технику "частичных сумм" немного с другой точки зрения. Для атаки на 8-тактовый Rijndael мы проверяем сумму значений одного байта из b⁽⁵⁾ по всем 2¹⁰⁴ шифрограммам кучи. Для этого мы вычислим значение выражения (1) пять раз: четыре раза на "нижнем уровне" и, используя эти четыре результата, в последний раз возьмем эти значения вместо криптограмм c_i,0,…,c_i,3. Каждое вычисление выражения (1) начинается со счетчиков (c₀,…,c₃,<…>), где байты c_i и соответствующие им ключи выровнены в одном и том же стобце. Вся процедура может быть поделена на следующие шаги:

• Угадывание двух байт ключа (назовем их k₀ и k₁) и вычисление счетчиков по молулю 2 для (c₀,…,c₃,<…>).

• Угадывание одного байта ключа (назовем его k₂) и подсчет (x_0,1,2,c₃,<…>).

• Угадывание одного байта ключа (назовем его k₃) и подсчет (x_0,…,3,<…>).

Заметим, что мы всего лишь ввели слегка отличное обозначение для x_<…>. Причина этого будет разъяснена позже.

Для атаки на 8-тактовый Rijndael со 192-битным ключом мы получаем 2¹²⁸-2¹¹⁹ текстов, угадываем 4 байта подключа первого такта для формирования куч, сосредотачиваем силы на одной куче, нацеливаясь на один байт из b⁽⁵⁾. Далее, угадываем три столбца из k⁽⁸⁾ и вычисляем значение выражения (1) для каждого столбца. Это дает нам получить 2⁵⁶ счетчиков по модулю 2 для (x_0,…,3,x_4,…,7,x_8,…,11,c₁₂,c₁₃,c₁₄,c₁₅). Заметим, что значения x_0,…,3, x_4,…,7 и x_8,…,11 связаны с байтами c₀, c₁, и c₂, которые используются в выражении (1) для вычисления последнего счетчика для байта из b⁽⁵⁾. Теперь мы вычислим (а не угадаем!) два байта из k⁽⁷⁾ и выполним первый шаг из структуры техники частичных сумм. По существу, мы уменьшили число счетчиков с 2⁵⁶ до 2⁴⁸, и подсчитаем значение по модулю 2 для (x_0,…,7,x_8,…,11,c₁₂,c₁₃,c₁₄,c₁₅). Угадаем последний столбец k⁽⁸⁾ и подсчитаем 2²⁴ значений для (x_0,…,7,x_8,…,11,x_12,…,15). Угадав два других байта из k⁽⁷⁾, мы получим 2⁸ счетчиков для x₁₅. Мы можем вычислить один байт из k⁽⁶⁾, который даст нам возможность проверить неравномерность одного байта из b⁽⁵⁾.

Заметим, что последовательность действий критична в свете временной сложности. Если мы сначала угадывали все 16 байт k⁽⁸⁾, а только потом вычисляли значения двух байт k^(7)', то ускорение работы возросло бы всего лишь в 2⁸ степени раз по сравнению в атакой на Rijndael с 256-битным ключом. По этой причине временная сложность для 192-битного ключа составляет 2¹⁹⁶, то есть медленне, чем прямой перебор.

3. Заключение.

Square - атака может быть улучшена так, что потребует времени порядка 2⁴⁴ шифрований для атаки 6-ти тактов Rijndael. Расширение до 7-ми тактов имеет сложность порядка 2¹⁵⁵ для 192-битного ключа и около 2¹⁷² для 256-битного ключа. Альтернативная атака на 7-тактовый алгоритм может быть применена при любой длине ключа со сравнительно низкой сложностью (2¹²⁰ шифрований), но она требует полный набор шифрограмм (2¹²⁸-2¹¹⁹ текстов). Другой результат нашего анализа показывает, что как для 192-битного ключа, так и для 256-битного, можно взломать 8-тактовый Rijndael быстрее, чем прямым перебором, имея 2¹²⁸-2¹¹⁹ текстов. При этом 256-битный ключ требует затрат, эквивалентных 2²⁰⁴ шифрований, а 192-битный - 2¹⁸⁸ шифрований.

2. Задача ключеформирования.

Ключеформирование в Rijndael является большим, чем специальной конструкцией. Оно имеет намного меньшую диффузию структуры, чем сам шифр, и содержит относительно немного нелинейных элементов.

1. Частичное отгадывание ключа.

Официальное описание Rijndael говорит, что ключеформирование проектировалось с учетом следущего требования: "Знание части ключа или подключа не позволяет вычислить множество остальных бит подключа". В процессе нашего анализа процедуры ключеформирования выяснилось, это требование не было успешно выполнено.

Давайте рассмотрим причины появления 128-битовго блока и 256-битового ключа более подробно. Ключеформирование содержит 8 тактов, которые генерируют все 15 тактовых ключей (последняя половина из последнего такта никогда не используется). Ключеформирование можно представить как четыре разделенные строки, которые связаны друг с другом. Обратим внимание на данную строку, к примеру с номером i. Мы угадаем значения K_i,7^(s) для s=0,…,6 (нет смысла угадывать его для s=7, так как этот байт никогда не используется в расширенном ключе). Используя реккурентное правило вычисления ключей, мы можем вычислить K_i,6^(s) для s=1,…,6, K_i,5^(s) для s=2,…,6 и так далее. В итоге мы получим 28 байт расширенного ключа, угадав только 7 байт.

Байты, которые мы угадали в строке i, те же, что влияют на строку с номером (i-1) mod 4. Разумеется, если мы отгадаем первые 8 байт строки с номером i-1, то сможем вычислить остаток этой строки до полных 60 байт, и если мы угадаем всего 15 байт, то мы узнаем 88 байт расширенного ключа.

Мы можем распространить это на более дальние строки и получить 148 байт ключа, угадав 23 байта, или получить 208 байт, угадав 31 байт. Разумеется, существует много путей к отгадыванию нескольких байт, чтобы узнать намного больше. Несколько атак из раздела 2 используют зависимость между байтами тактового ключа, чтобы уменьшить сложность атаки.

2. Разбиение ключа.

Другое интересное свойство ключа - возможность разбиения его на две половины. Две самые верхние строки взаимодействуют с двумя самыми нижними посредством только 14 байт (это и есть причина появления 128-битного блока и 256-битного ключа). Если мы угадали (или знали) эти 14 байт, то остальная часть ключа может быть разбита на две независимые части, каждая из которых контролирует половину байт расширенного ключа. Существует много вариантов для разбиения ключа. Самый простой путь - по строкам, но возможно и разбиение по столбцам (по крайней мере на некоторых тактах).

Это наводит на мысль о возможности атаки из класса "встречи посередине". Однако, так как байты расширенного ключа из двух половин очень тщательно перемешиваются в нелинейном шифре, мы не можем предложить пути для использования этого свойства. Заметим, что ключеформирование в DES позволяет разделить биты ключа на 56 независимых частей, но не известно атак, использующих это свойство.

3. Заключение.

Такие свойства, присутствующие в официальном проекте, не могут не настораживать. Некоторые из атак используют зависимости между байтами расширенного ключа и могли бы быть более сложны в исполнении, если бы этих зависимостей не было. Атака на 8-тактовый Rijndael со 192-битным ключом могла бы быть медленне, чем прямой перебор, без этих соотношений. Атаки, рассматриваемые в следующем разделе, так же используют эти свойства ключеформирования.

3. 9-тактовая ключезависимая атака.

В этом разделе расскзывается о применении ключезависимой атаки к 9-тактовому Rijndael с 256-битным ключом. Она базируется на одном из вариантов Square-атаки: мы используем 256 зависимых ключа, которые различаются только одним байтом в четвертом тактовом ключе. Также используются различия открытых текстов, чтобы убрать различия в более ранних тактовых ключах и получить три байта в конце 6-го такта, которые дадут ноль при суммировании по всем 256 шифрограммам. Мы угадаем байты тактовых ключей на последних трех тактах для обращения криптограмм и проверки этого свойства.

1. Структура зависимости ключей.

Начав с неизвестного базового ключа L, мы получим набор из 256 зависимых ключей L₀,…,L₂₅₅. Разность дает значение a в байтах 21 и 25, и ноль в остальных. Диффузия в ключеформировании достаточно мала, что дает возможность отслеживать все различия в тактовых ключах. Рисунок 1 показывает структуру этих различий. Ключеформирование для 9-тактового шифра требует генерации 10-ти тактовых ключей. При 128-битном блоке данных и 256-битном ключе это требует 5 циклов в процессе ключеформирования, что и отбражено на рисунке. На каждом такте генерируются два тактовых ключа.

Темно-серым цветом показаны те байты, которые нами угадываются, светло-серым цветом - те, которые выводятся из угаданных при помощи реккурентных соотношений между байтами расширенного ключа. В сумме мы угадываем 27 байт ключа и это позволяет нам вычислить 66 байт расширенного ключа. Мы можем использовать все наши догадки в процессе атаки, но в данный момент мы сконцентрируем внимание на на отслеживании различий в процессе ключеформирования.

На первом такте мы имеем разницу a в K_1,5⁽⁰⁾ и K_1,6⁽⁰⁾. На следующем такте мы получаем разницу a в K_1,5⁽¹⁾. На третьем такте мы имеет разницу a в K_1,5⁽²⁾, K_1,6⁽²⁾ и K_1,7⁽²⁾. В этой точке различия впервые сталкиваются с нелинейным S-box'ом. Для отслеживания различий нам необходимо знать K_1,7⁽²⁾; это даст нам возможность вычислить выходное различие b после S-box'а при входном различии a. Как показывают затенения на рисунке, этот байт ключа может быть вычислен исходя из тег догадок о первоначальном ключе, которые были нами сделаны. На четвертом такте мы получаем различие b в K_0,i⁽³⁾ для i=0,…,3. Тут мы снова сталкиваемся с S-box'ом и поэтому нам необходимо знать K_0,3⁽³⁾. Это даст нам выходное различие c после S-box'а при входном различии b. Таким образом, мы получам различие c в K_0,i⁽³⁾ для i=4,…,7. Различия из предыдущего такта также учитываются, что дает разницу a в K_1,5⁽³⁾ и в K_1,7⁽³⁾. Мы можем отследить остальные распостранения различий простым образом так, как показано на рисунке. В итоге оказывается, что мы угадали байтов больше, чем требовалось для отслеживания изменений. Само собой, для каждого значения a мы знаем точные значения b, c, d, e, f и g. Мы угадывали большее количество байт, которые нам нужны при осуществлении атаки, для отслеживания изменения нам необходимо было угадать только 6 байт в порядке отслеживания структуры зависимостей в процессе ключеформирования.

K(0)
						a	a

K(1)
						a

K(2)
						a	a	a

K(3)	b	b	b	b	c	c	c	c
						a		a

K(4)	bd	d	bd	d	cf	f	cf	f
						a	a
	e	e	e	e	g	g	g	g

Рисунок 1. Структура различий ключей в 9-тактовой атаке.

2. Шифрограммы.

Угадав байты, выделенные темно-серым цветом на рисунке 1, мы шифруем один открытый текст на каждом из ключей. Эти открытые тексты вибираются так, что все шифрограммы заканчивались одной и той же последовательностью данных после первого такта (т.е. после добавления второго тактового ключа). Мы знаем отличие второго тактового ключа и отгаданные байты ключа, что позволяет нам вставить подходящие отличия в открытый текст, чтобы гарантировать одинаковые окончания после первого такта. Теперь мы получим различие в одном байте, вставленном в конце такта 3. Если мы посмотрим на все 256 шифрограмм, то заметим, что этот один байт принимает каждое значение только один раз. Это гарантирует то, что каждый байт b⁽⁵⁾ примет все возможные значения, если учитывать все 256 шифрограмм.

Следующие несколько шагов отображены на рисунке 2. Тактовые ключи для тактов 5 и 6 показаны слева; их различия выделены. Справа показаны некоторые различия данных. Байты, помеченные символом "O", принимают все возможные значения только один раз. Байты, помеченные символом "X", ведут себя как им угодно. Байты, помеченные символом "", в сумме по всем 256 шифрограммам дают ноль. Обратим внимание, что мы имеем три таких байта в b⁽⁶⁾.

Начнем вычисление b_1,3⁽⁵⁾ из открытого текста, известных и дополнительно угаданных байт ключа. На рисунке они выделены серым цветом. Заметим, что мы используем эквивалентное представление для 8-го такта, где мы поменяли местами перемешивание столбцов и добавление тактового ключа, а также добавляем k^(8)' вместо k⁽⁸⁾. Нам известна шифрограмма и последний тактовый ключ, поэтому мы можем обратить операцию добавления ключа в 8-ом такте. Теперь мы угадаем 4 выделенных байта из k^(8)' (хотя мы и знаем некоторые байты из k⁽⁸⁾, но мы не можем получить из них никакой информации о k^(8)'. Несмотря на это, так как каждый столбец k^(8)' получается в результате инверсии операции перемешивания столбцов над k⁽⁸⁾, то мы можем распространить наши знания о различиях с k⁽⁸⁾ на k^(8)'). Теперь мы можем вычислить выделенные байты t⁽⁸⁾, s^(8)' и t^(7)', и в завершении мы можем рассчитать b_1,3⁽⁶⁾. Проверим, дают ли эти значения в сумме по всем 256 шифрограммам ноль. Если этого не происходит, значит одна из наших догадок была неверна. Как и раньше, мы можем сгенерировать достаточное количество наборов открытых текстов для однозначной идентификации корректности сделагнной нами догадки о байтах ключа.

В конце концов мы угадаем 31 байт ключа, и для каждой догадки затратим время порядка одной шифрации. Это даст суммарную сложность атаки порядка 2²⁴⁸.

Глядя на требования к открытым текстам, нам не надо выполнять 256 шифрований для каждого угадываемого байта ключа. Восемь байтов открытого текста, которые мы используем для уничтожения различий принимают только 2⁶⁴ значений, поэтому мы можем шифровать только 2⁶⁴ открытых текстов для каждого из 256 ключей. Общие затраты при этом составляют 2⁷².

3. Усовершенствование.

Мы можем использовать технику из раздела 2.3 для усовершенствования атаки. Вместо угадывания восьми байт ключа первого такта мы используем все 2⁶⁴ открытых текста для каждого из ключей и просуммируем по всем 2⁷² шифрограммам. Нам потребуется поряка 32 структур по 2⁷² текстов для однозначной идентификации правильного предположения, поэтому информационная сложность возрастает до 2⁷⁷. Теперь мы угадаем 19 темно-серых байт (152 бита) из K⁽⁴⁾ рисунка 1. Это также дает необходимую информацию для отслеживания различий между 256 ключами. Расшифруем каждую из 2⁷² шифрограмм одной структуры для одного такта, и подсчитаем, как часто встречается каждое из вохзможных значений в интересующих нас 4-х байтах. Теперь мы можем рассчитать выражение (1), что потребует порядка 2⁴⁸ шифрований. Ясно, что именно этот процесс будет доминировать в оценке работы по расшифровке последнего такта. Это уменьшает сложность атаки до 5*2²²⁴; множитель "5" вытекает из того факта, что нам нужно пять структур, прежде чем мы начнем отсекать догадки, что увеличивает сложность атаки.

4. Дальнейшая работа.

Существует множество путей для изменения этой атаки, таких как разных структур различия ключей или возможности применения техники "частичных сумм" для уменьшения сложности атаки. Мы не изучали детально эти возможности.

5. Заключение

Здесь была описана ключезависимая атака на 9-тактовый Rijndael c 256-битным ключом, которая использует 2⁷⁷ открытых текстов и требует времени порядка 2²²⁴ шифрований.



k(5)
	a	a	a

k(6)
b	b	b	b

k(7)

k(8)'

k(9)

Рис.2.

m(5)
O	O	O	O
O	O	O	O
O	O	O	O
O	O	O	O

m(6)
X	X	X	
X	X	X	
X	X	X	
X	X	X	

t(7)

s(8)

Такты 6-9 атаки

b(5)
O	O	O	O
O	X	X	X
O	O	O	O
O	O	O	O

b(6)
X	X	X	X
X	X	X	
X	X	X	
X	X	X	

t(8)

3. Результаты исследований.

Мы исследовали безопасность Rijndael и описали несколько новых атак и неожиданных свойств шифра. Вплоть до нынешнего момента мы имели лишь версию Rijndael со 128-битным ключом. Несмотря на сходность структуры, Rijndael с большим размером блока имеет довольно много отличий - к примеру, различается выравнивание байтов, которое критично для некоторых из наших атак, - поэтому мы предпочитаем анализировать их раздельно.

Мы ввели понятие техники "частичных сумм", которая по существу служит для снижения сложности Square - атаки. Также было показано, как можно уменьшить временную сложность за счет увеличения информационной для проникновение в более глубокие такты Rijndael. Эта техника позволяет нам найти атаки, которые позволят взломать более чем 7 (из 10) тактов для 128-битного ключа, 8 (из 12) для 192-битного ключа и 8 (из 14) для 256-битного ключа. Некоторые из этих атак требуют для реализации полную шифровальную книгу и поэтому не имеют практического применения.

Задача ключеформирования не удовлетворяет своим опубликованным показателям для 192-битного и 256-битного ключей. Несмотря на это мы не видим больших возможностей для использования свойств ключеформирования, описанных в разделе 3; мы просто считаем это настораживающим.

9-тактовая ключезависимая атака имеет сложность порядка 2²²⁴, что является причиной ее почти полной практической непригодности; но тем не менее, она работает быстрее, чем полнный перебор, который является стандартным критерием для сравнивания производительности. Наши результаты не имеют практического смысла для использования с полным Rijndael.

Приложение А. Обозначения.

Оригинальное описание Rijndael использует символы для определения шифра и несколько раз переопределяет их. Это делает неудобным явным образом ссылаться на конкретные названия переменных шифра. Для решения этой проблемы мы определяем некоторые дополнительные термины и символы для различных объектов, используемых в шифре. Для полноты картины мы присваиваем имя каждому промежуточному значению, которое нами используется. Некоторые из этих обозначений не используются в этом описании, но приведены для полного понимания ситуации.

3a Байт 3a₁₆ (или любое другое значение байта). Может использоваться как для непосредственного указания значения байта, так и интерпретироваться как элемент из GF(2).

a_i,j^(r) Байт в позиции (i,j) на начало такта r.

b_i,j^(r) Байт в позиции (i,j) на выходе такта r (сразу после добавления ключа).

c(x) Полином 03x³+01x²+01x+02, который используется для определения MDS-матрицы.

c_i Байты шифртекста, где i  {0,…,4N_b-1}.

C_i Число позиций, на которое сдвигается влево строка i в операции сдвига строк.

k_i,j^(r) Байт расширенного ключа в позиции (i,j) в такте r, где r  {0,…,N_r}, i  {0,…,3}, и j  {0,…,N_b-1}. Для r = 0 это ключ, который XORится с данными перед первым тактом. Весь ключ обозначается как k^(r).

k_i,j^(r)' Это простая линейная функция от ключа k^(r). XOR ключа k_i,j^(r)' с данными до перемешивания строк эквивалентна XOR ключа k_i,j^(r) сданными после перемешивания.

K_i Байты расширенного ключа в обычном порядке, где i  {0,…,4N_b(N_r+1)-1}. Байты K₀,…,K_4Nk-1 представляют собой непосредственно ключ шифра.

K_i,j^(s) Байт расширенного ключа в позиции (i,j) в цикле s, где s  {0,…,N_s}, i  {0,…,3}, и j  {0,…,N_k-1}.

m_i,j^(r) Байт в позиции (i,j) в такте r на выходе операции перемешивания столбцов.

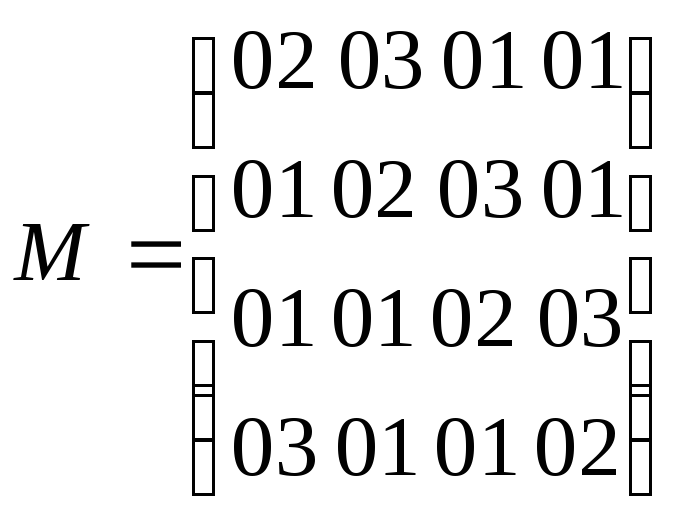
M MDS-матрица.

N_b Размер блока в битах, деленный на 32.

N_k Размер ключа в битах, деленный на 32.

N_r Число тактов.

N_s Число циклов расширения ключа; N_s = (N_r+1)N_b/N_k.

p_i Байт открытого текста, где i  {0,…,4N_b-1}.

r Номер такта. Такты нумеруются с 1 до N, и значение 0 иногда используется для обозначения первоначального суммирования с тактовым ключом.

R_i^(s) Константа такта, используемая в позиции (i,0) в цикле s.

s Номер цикла в процессе расширения ключа. Каждый цикл производит 4N_k байт расширенного ключа. Циклы нумеруются с 0 до N_s-1.

s_i,j^(r) Байт на позиции (i,j) в такте r на выходе S-box`а.

S S-box. Иногда обозначается как S[x]. Обратный S-box обозначается как S^-1.

t_i,j^(r) Байт на позиции (i,j) на такте r на выходе операции сдвига строк.

Заметим, что составляющие операции ключеформирования мы называем "циклами" в отличие от "тактов" непосредственно шифрования. Такие обозначения применяются именно для того, чтобы подчеркнуть принадлежность этих понятий к двум различным процедурам. Если размер блока данных и размер ключа совпадают, то эти два параметра равны между собой, но в общем случае это неверно.

Теперь мы можем дать некоторые формулы, связывающие эти величины между собой. Этот раздел есть и в полном описании шифра, но там он слишком труден для восприятия. Заметим, что N_b и N_k - это значения параметров шифра, каждый из которых может принимать одно из значений 4, 6 или 8. Произведение двух байт определяется как произведение в GF(2)[x]/(x⁸+x⁴+x³+x+1), а значение байта , гдеa_i  GF(2), отождествляется с элементом поля .

a_i,j⁽¹⁾ = p_4j+ik_i,j⁽⁰⁾ Начальное добавление ключа.

s_i,j^(r) = S[a_i,j^(r)] Замещение байтов.

t_i,j^(r) = s_{i,(j+Ci) mod Nb}^(r) Сдвиг строки.

[m_0,j^(r),…,m_3,j^(r)]^T = M[t_0,j^(r),…,t_3,j^(r)]^T Перемешивание столбцов.

b_i,j^(r) = m_i,j^(r) Добавление тактового ключа.

a_i,j^(r) = b_i,j^(r-1) Для r = 2,…,N_r.

c_4j+i = t_i,j^(Nr)k_i,j^(Nr) Последний такт.

K_i,j^(r) = K_4rNb+4j+i Тактовые ключи.

K_4sNb+4j+i = K_i,j^(s)

K_i,0^(s) = K_i,0^(s-1)R_i^(s)S[K(_{i+1) mod 4,Nk-1}^(s-1)] для s = 1,…,N_s-1.

K_i,4^(s) = S[K_i,3^(s)]K_i,j^(s-1) Если N_k = 8.

K_i,j^(s) = K_i,j-1^(s)K_i,j^(s-1) Если j>8 и (j  4 V N_k  8).

C_i = i + i/2 * N_b/8 Для i = 0,…,3.

N_r = max(N_b, N_k) + 6 Число тактов.

R_i^(s) = 0 Для i > 0.

R₀^(s) = элемент поля x^s-1