Московский Государственный Институт э лектронной Техники
Курсовой проект
По предмету: Компьютерное моделирование интегральных приборов
Тема: Компаратор с последовательным сравнением 4-х разрядных чисел
Разработал: студент гр.ЭКТ-36
Проверила: Артамонова Е.А.
МОСКВА
2005
Схемы сравнения (Двоичные компараторы)
Для
сравнения операндов в цифровых схемах
часто используют специальные схемы –
двоичные компараторы. Простейшим
вариантом компаратора являются схемы
для определения равенства двух операндов
и
.
Равенство одноразрядных операндов
определяется с помощью логической
операции Равнозначность:
при
,
при
.
Для определения равенства многоразрядных
операндов выполняется конъюнкция
результатов сравнения отдельных
разрядов:
Более
сложными являются схемы сравнения для
определения неравенства
разрядных
операндов
и
:
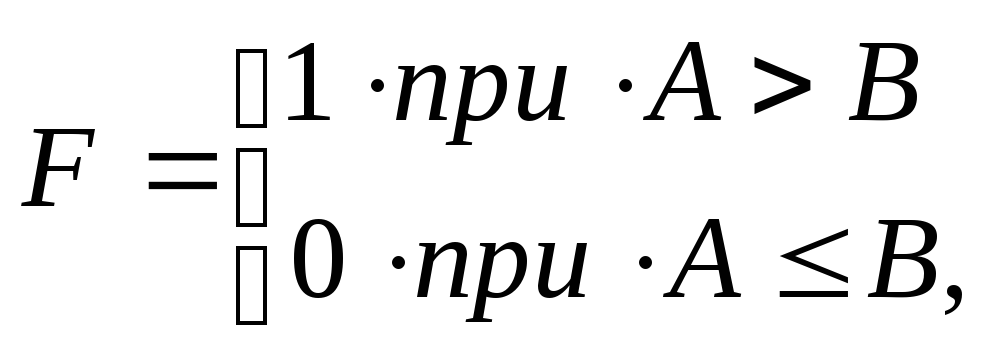
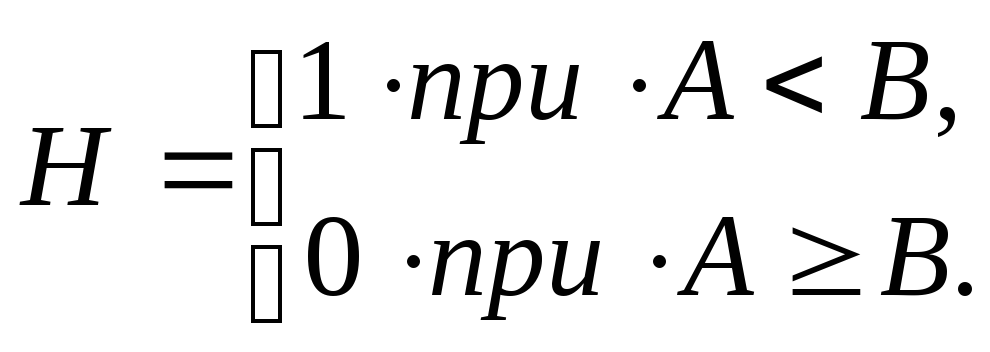
Для
одноразрядных операндов
и
функции сравнения реализуются с помощью
операций Запрет:
,
.
Для
двухразрядных операндов
и
функции неравенства
и
определяются таблицей истинности (см
таблицу). Минимизируя выражения функций
с помощью карт Карно, получаем:
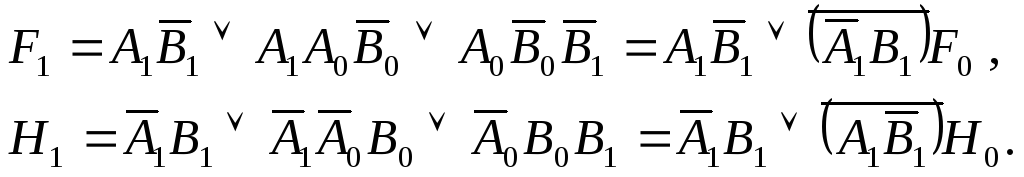
Аналогично
представляются функции сравнения
разрядных
операндов:
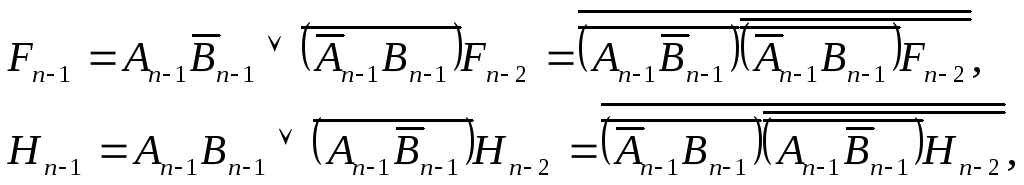
где
функции
сравнения
младших разрядов.
Согласно
последним выражениям сравнение операндов
можно производить последовательно,
начиная с младших разрядов
Пример многоразрядного компаратора с
последовательной структурой, реализованного
в соответствии с выражением для
,
дан на первом рисунке. Общая задержка
формирования сигнала
для этой схемы составляет
Поэтому при большом числе разрядов
компараторы с последовательной структурой
имеют низкое быстродействие.
Таблица
истинности сравнения двухразрядных
чисел
и
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
В быстродействующих компараторах реализуется одновременное (параллельное) сравнение всех разрядов операндов в соответствии со следующими выражениями.
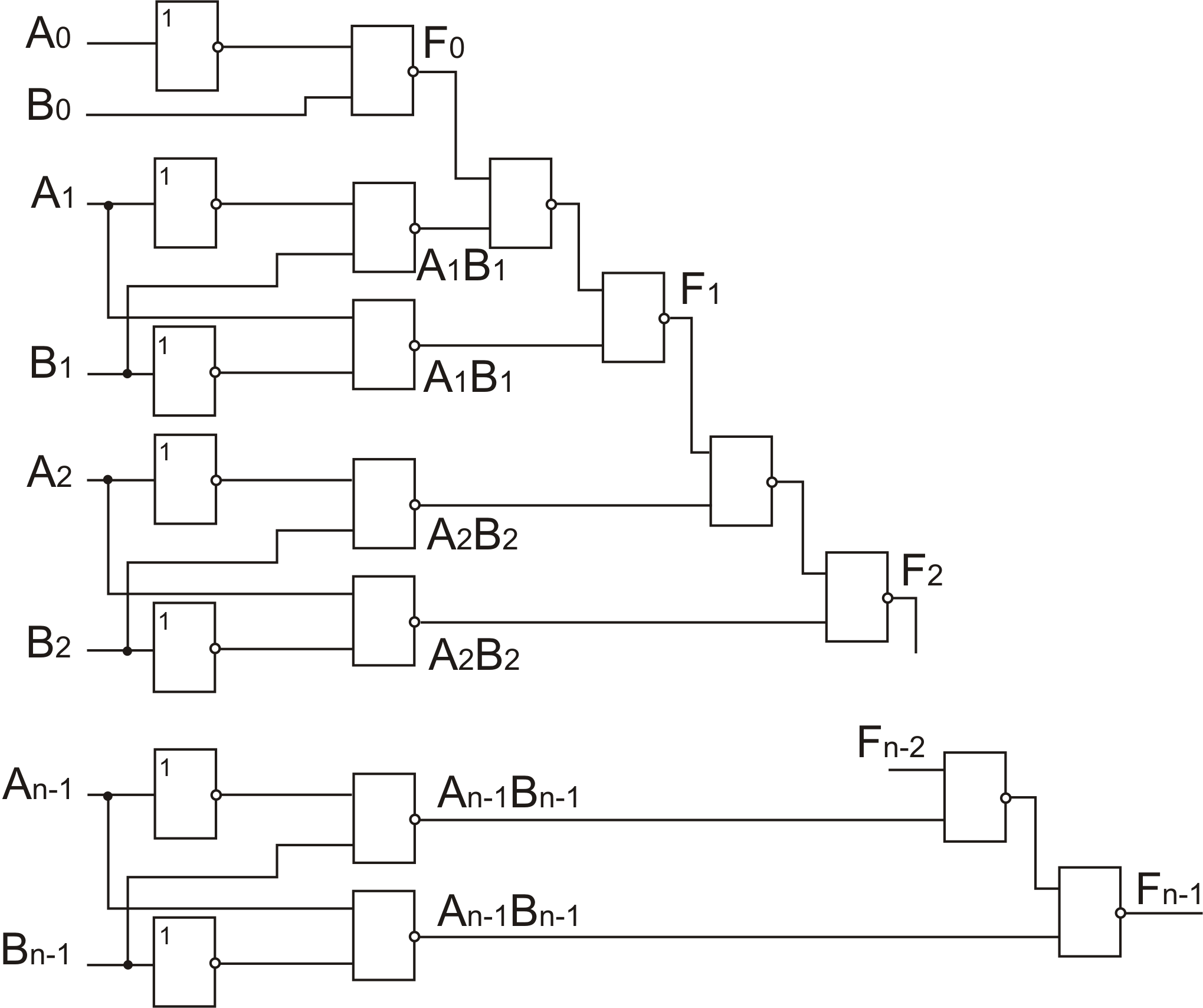
Рис.1
Схема компаратора с последовательным сравнением разрядов