Схемы сравнения (Двоичные компараторы)
Для
сравнения операндов в цифровых схемах
часто используют специальные схемы –
двоичные компараторы. Простейшим
вариантом компаратора являются схемы
для определения равенства двух операндов
и
.
Равенство одноразрядных операндов
определяется с помощью логической
операции Равнозначность:
при
,
при
.
Для определения равенства многоразрядных
операндов выполняется конъюнкция
результатов сравнения отдельных
разрядов:
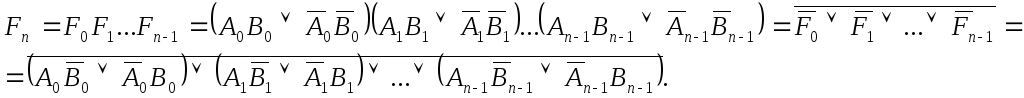
Более
сложными являются схемы сравнения для
определения неравенства
разрядных
операндов
и
:
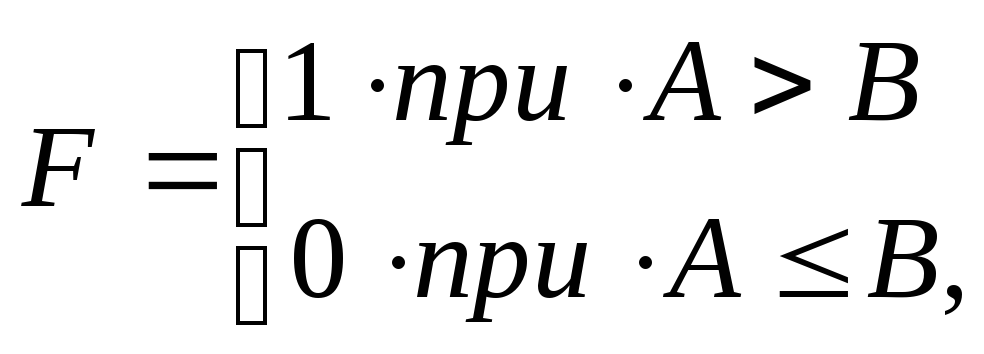
Для
одноразрядных операндов
и
функции сравнения реализуются с помощью
операций Запрет:
,
.
Для
двухразрядных операндов
и
функции неравенства
и
определяются таблицей истинности (см
таблицу). Минимизируя выражения функций
с помощью карт Карно, получаем:
Аналогично
представляются функции сравнения
разрядных
операндов:
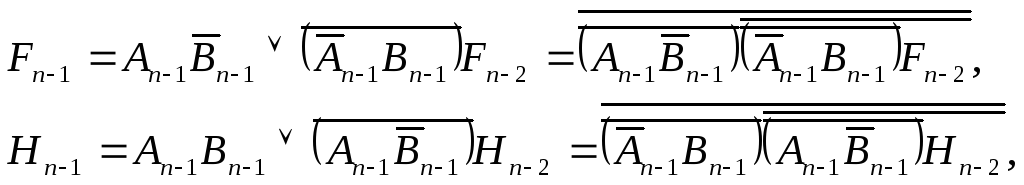
где
функции
сравнения
младших разрядов.
Согласно
последним выражениям сравнение операндов
можно производить последовательно,
начиная с младших разрядов
Пример многоразрядного компаратора с
последовательной структурой, реализованного
в соответствии с выражением для
,
дан на первом рисунке. Общая задержка
формирования сигнала
для этой схемы составляет
Поэтому при большом числе разрядов
компараторы с последовательной структурой
имеют низкое быстродействие.
Таблица
истинности сравнения двухразрядных
чисел
и
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
В быстродействующих компараторах реализуется одновременное (параллельное) сравнение всех разрядов операндов в соответствии со следующими выражениями.
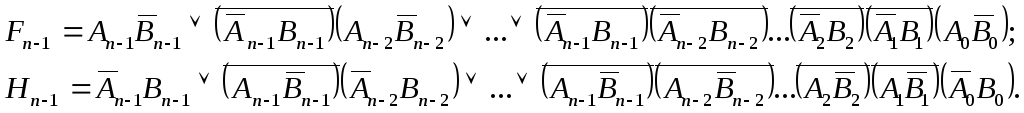
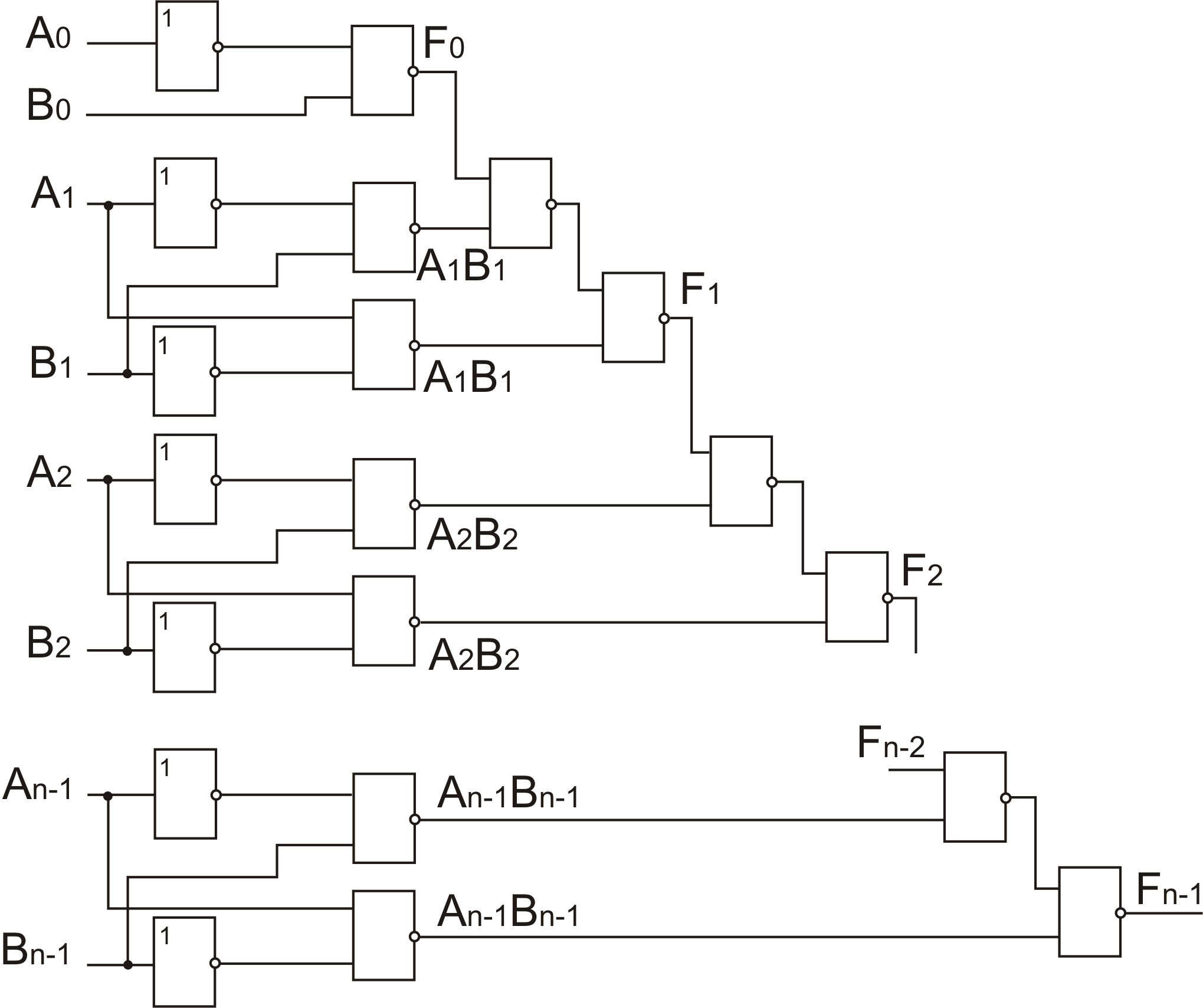
Рис.1
Схема компаратора с последовательным сравнением разрядов
Компаратор с последовательным сравнением 4-х разрядных чисел
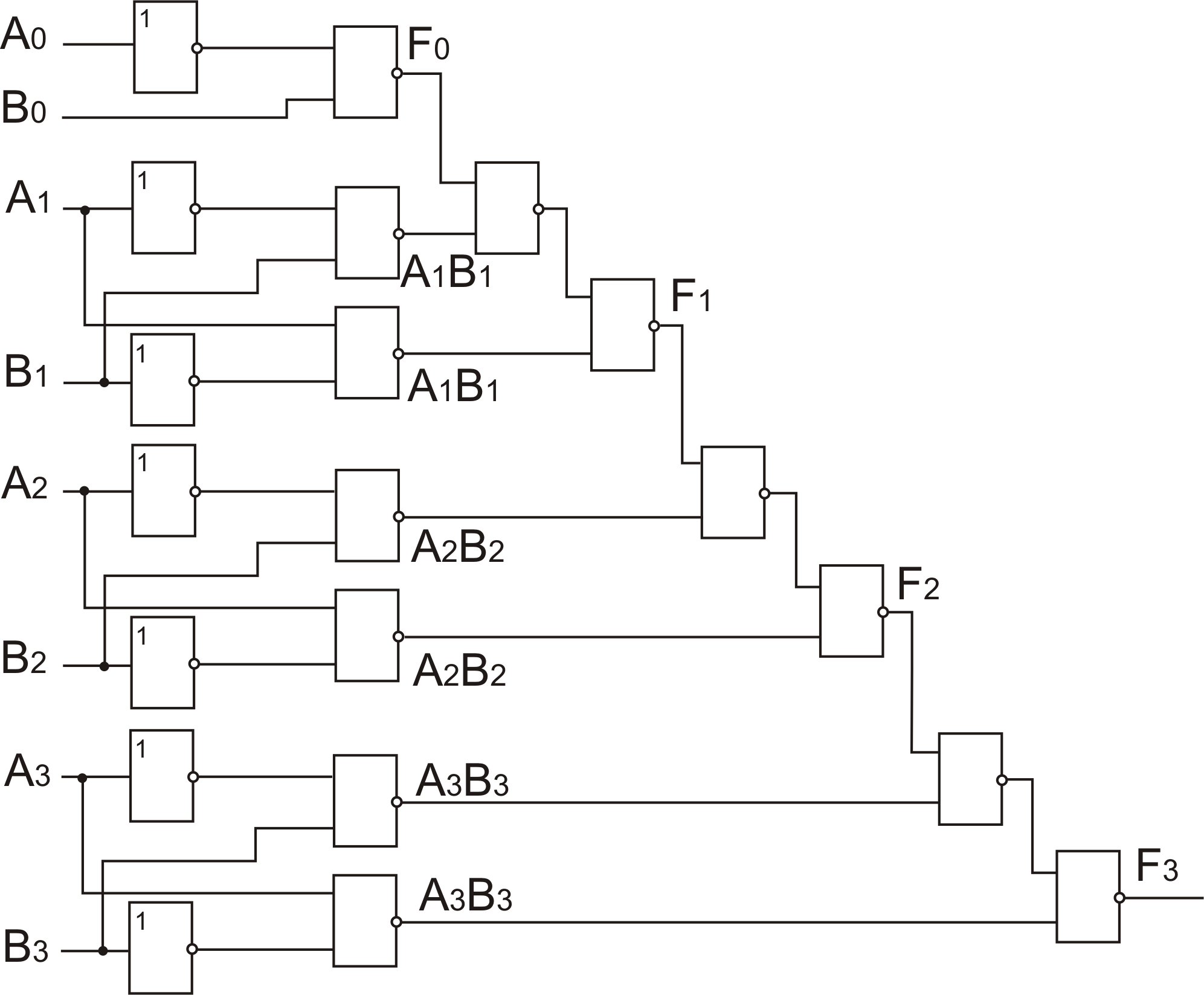
Техническое задание:
|
Технологический базис |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,
Предварительный расчет параметров транзисторов
-
-
,
,
-
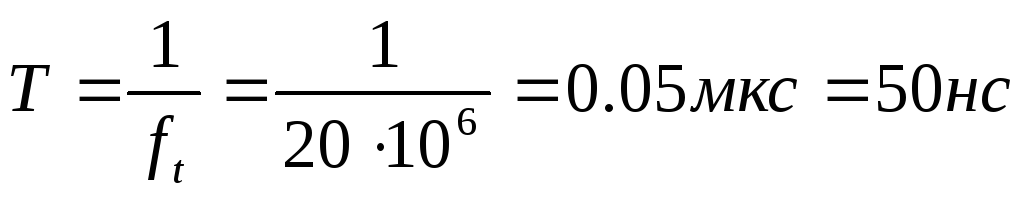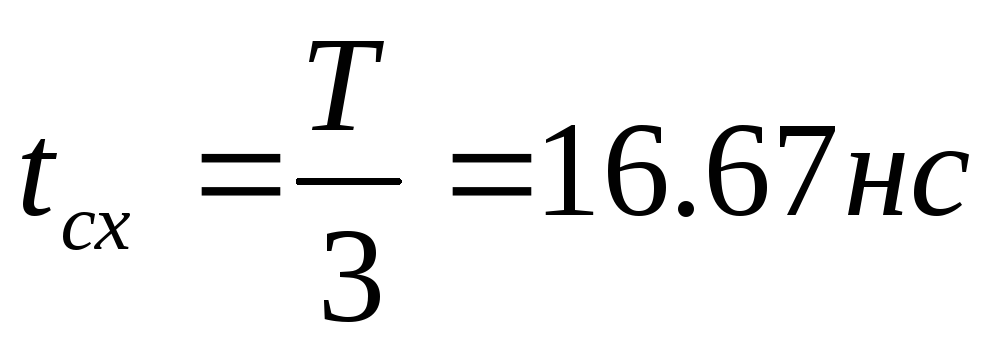Полагая, что
,
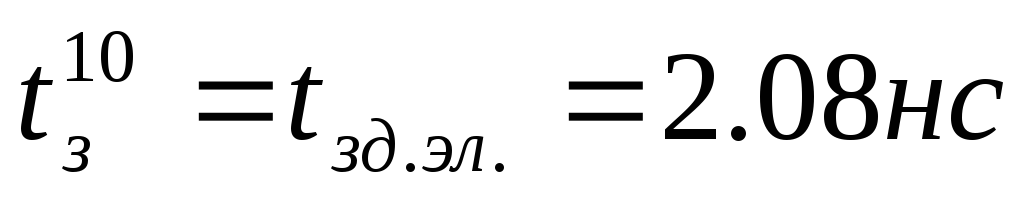получим
Исследование переходных процессов в логических элементах
-
Инвертор
,
,
,
,
,
-
2 ИЛИ-НЕ
,
,
,
,
,
-
2 И-НЕ
,
,
,
,
,
Определение паразитной емкости
Значение емкости оценим по формуле
,
где
толщина
межслойной изоляции,
,
площадь
обкладок паразитного конденсатора,
-абсолютная
диэлектрическая проницаемость
диэлектрика,
=
,
-
относительная диэлектрическая
проницаемость диэлектрика,
.
что
составляет меньше
от значения
.
Следовательно, в
дальнейшем мы влияние паразитной
емкости учитывать не будем.
Расчет допустимой максимальной длины участка межсоединения
Оптимизация КМДП цепи при работе на большую емкостную нагрузку
коэффициент
масштабирования
число
последовательно соединенных инверторов
Выводы
В итоге разработки устройства мы получили следующее:
-
элемент Инвертор
имеет топологическую площадь равную
,
,
,
-
элемент 2И-НЕ
имеет топологическую площадь равную
,
,
,
-
элемент 2ИЛИ-НЕ
имеет топологическую площадь равную
,
,
,
-
общая площадь устройства равна
,из-за
малости значения паразитной емкости
по сравнению с значением
,
мы ей пренебрегли.
Выходной каскад может быть оптимизирован путем замены на цепочку последовательно соединенных 5ти инверторов с коэффициентом масштабирования 2,456.