4.2. Дискретно-непрерывные каналы

Дискретно-непрерывный канал имеет дискретный вход и непрерывный выход. Примером такого канала является канал, образованный совокупностью технических средств между выходом кодера канала и входом демодулятора. Для его описания необходимо знать алфавит входных символов ,, вероятности появления символов алфавита, полосу пропускания непрерывного канала, входящего в рассматриваемый канал и плотности распределения вероятностей (ПРВ)появления сигналана выходе канала при условии, что передавался символ.

Зная вероятности и ПРВпо формуле Байеса можно найти апостериорные вероятности передачи символа:

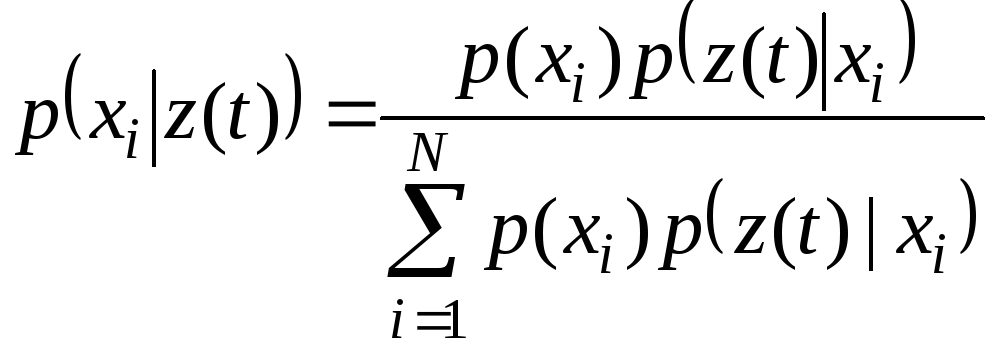. (4.8)

Решение о переданном символе обычно принимается из условия максимума .

4.3. Дискретные каналы

Примером дискретного канала без памяти может служить -ичный канал. Канал передачи полностью описывается если заданы алфавит источника,, , вероятности появления символов алфавита, скорость передачи символов, алфавит получателя,, и значения переходных вероятностейпоявления символапри условии передачи символа.

Первые две характеристики определяются свойствами источника сообщений, скорость – полосой пропускания непрерывного канала, входящего в состав дискретного. Объем алфавита выходных символов зависит от алгоритма работы решающей схемы; переходные вероятностинаходятся на основе анализа характеристик непрерывного канала.

Стационарным называется дискретный канал, в котором переходные вероятности не зависят от времени.

Дискретный канал называется каналом без памяти, если переходные вероятности не зависят от того, какие символы передавались и принимались ранее.

В качестве примера рассмотрим двоичный канал (рис. 4.6). В этом случае , т.е. на входе канала алфавит источника и алфавит получателя состоит из двух символов «0» и «1».

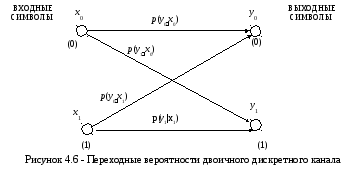
Алфавит входных сигналов имеет два символа х₀ и х₁ . Выбранный случайным образом источником сообщений, один из этих символов подаётся на вход дискретного канала. На приёме регистрируется у₀ и y₁. Выходной алфавит тоже имеет два символа. Символ у₀ может быть зарегистрирован при передаче сигнала х₀ . Вероятность такого события – р(y_0x₀). Символ у₀ может быть зарегистрирован при передаче сигнала х₁. Вероятность такого события – р(y_0x₁). Символ y₁ может быть зарегистрирован при передачи сигналов х₀ и х₁ с вероятностями р(y_1x₀) и р(y_1 x₁) соответственно. Правильному приёму соответствуют события с вероятностями появления р(y_1x₁) и р(y_0x₀). Ошибочный прием символа происходит при появлении событий с вероятностями р(y_1x₀) и р(y_0x₁). Стрелки на рис. 4.6 показано, что возможные события заключаются в переходе символа х₁ в y₁ и х₀в y₀ (это соответствует безошибочному приему), а также в переходе х₁ в y₀ и х₀в y₁ (это соответствует ошибочному приему). Такие переходы характеризуются соответствующими вероятностями р(y_1x₁), р(y_0x₀), р(y_1x₀), р(y_0x₁), а сами вероятности называют переходными. Переходные вероятности характеризуют вероятности воспроизведения на выходе канала переданных символов.

Канал без памяти называют симметричным, если соответствующие переходные вероятности одинаковы, а именно одинаковы вероятности правильного приёма, а также одинаковы вероятности любых ошибок. То есть:

- правильный прием,

- ошибочный прием.

Для общего случая

(4.9)

Необходимо отметить, что в общем случае в дискретном канале объемы алфавитов входных и выходных символов могут не совпадать. Примером может быть канал со стиранием (рис. 4.7). На рис. 4.7 введены обозначения: - вероятность ошибочного приема, - вероятность стирания, - вероятность правильного приема. Алфавит на его выходе содержит один добавочный символ по сравнению с алфавитом на входе. Этот добавочный символ (символ стирания «?») появляется на выходе канала тогда, когда анализируемый сигнал не удается отождествить ни с одним из передаваемых символов. Стирание символов при применении соответствующего помехоустойчивого кода позволяет повысить помехоустойчивость.

Большинство реальных каналов имеют «память», которая проявляется в том, что вероятность ошибки в очередном символе зависит от того, какие символы передавались до него и как они были приняты. Первый факт обусловлен межсимвольными искажениями, являющимися результатом рассеяния сигнала в канале, а второй – изменением отношения сигнал-шум в канале или характера помех.

В постоянном симметричном канале без памяти условная вероятность ошибочного приема ()-го, символа если-й символ принят ошибочно, равна безусловной вероятности ошибки. В канале с памятью она может быть больше или меньше этой величины.

Наиболее простой моделью двоичного канала с памятью является марковская модель, которая задается матрицей переходных вероятностей:

,

где – условная вероятность того, что принят ()-й символ ошибочно, если-й принят правильно; 1-– условная вероятность того, что принят ()-й символ правильно, если-й принят правильно;– условная вероятность того, что принят ()-й символ ошибочно, если-й принят ошибочно; 1-– условная вероятность того, что принят ()-й символ правильно, если-й принят ошибочно.

Безусловная (средняя) вероятность ошибки в рассматриваемом канале должна удовлетворять уравнению:

,

или

.

Данная модель имеет достоинство – простоту использования, не всегда адекватно воспроизводит свойства реальных каналов. Большую точность позволяет получить модель Гильберта для дискретного канала с памятью. В такой модели канал может находиться в двух состояниях и. В состоянииошибок не происходит; в состоянииошибки возникают независимо с вероятностью. Также считаются известными вероятности перехода из состояния ви вероятности перехода из состояния в состояние. В этом случае простую марковскую цепь образует не последовательность ошибок, а последовательность переходов:

.

При этом достаточно легко выразить безусловные вероятности нахождения канала в состояниях и:

,

.

Безусловная вероятность ошибки в этом случае может быть определена по формуле:

.

Наиболее часто при использовании модели Гильберта для двоичного канала полагают , т.е. состояниерассматривается как полный обрыв канала связи. Это согласуется с представлением о канале, в котором действуют коммутационные помехи.

Возможен другой подход к построению математических моделей каналов, при котором вся предыстория до некоторого фиксированного момента времени заменяется заданием некоторого начального состояния цепи. Зная характеристики цепи, начальное состояние и сигнал, действующий только на промежутке отдо, можно определить сигнал на выходе и новое состояние цепи в любой момент времени.

Состоянием цепи называется минимальное множество величин, в которое входит элементов, однозначно определяющих поведение цепи в момент времени. Элементы этого множества называют переменными состояния, которые обычно рассматривают как составляющие компоненты-мерного вектора. Для любой цепи можно записать два уравнения, позволяющих по состоянию в моменти сигналу, поступающему на вход, найти выходной сигнал и состояние в момент. Эти матричные уравнения называют уравнением состояния и уравнением наблюдения.

ВОПРОСЫ И ЗАДАНИЯ

1. Что такое непрерывный канал связи?

2. Что такое дискретный канал связи?

3. Что такое канал передачи данных?

4. Запишите математическую модель канала с аддитивным шумом.

5. Запишите математическую модель канала с затуханием, запаздыванием и гауссовским белым шумом.

6. Запишите математическую модель канала с неопределенной фазой сигнала.

7. Запишите математическую модель инерционного канала.

8. Что из себя представляет многолучевый инерционный канал с переменными параметрами?

9. За счет чего возникает многолучевость в многолучевом канале?

10. Что такое стационарный дискретный канал?

11. Каким образом определяются апостериорные вероятности появления символов на выходе дискретного канала?

115