4.2. Методы повышения эффективности алгоритмов

Эффективность алгоритма определяется мерой близости к оптимальному значению его критерия качества, под которым понимается минимум временной либо емкостной сложности; в сложных случаях используют составной критерий, включающий в себя оба параметра сложности с некоторыми выбранными весами. Ясно, что с увеличением размера задачи, для которой разрабатывается алгоритм, все более важной становится проблема эффективности алгоритма. Заметим здесь же, что построение эффективного алгоритма для конкретной задачи тесно связанно с выбором подходящих структур данных этой задачи.

Существует большое число приемов, иногда очень хитроумных, построения эффективных алгоритмов для конкретных задач. В то же время наработано небольшое число методов построения эффективных алгоритмов, которые применимы ко многим задачам и даже их классам. Ниже рассматриваются основные из этих методов.

4.2.1. Рекурсия.

Процедуру, которая прямо или косвенно обращается к себе, называют рекурсивной. Применение рекурсии часто позволяет давать более ясные и сжатые описания алгоритмов, чем это было бы возможно без рекурсии.

Рекурсия является особенно мощным средством в математических определениях. В качестве примеров рассмотрим определения натуральных чисел, древовидных структур и функции факториал:

1. Натуральные числа:

а) 1 есть натуральное число;

б) целое число, следующее за натуральным, есть натуральное число (х'=x+1).

2. Древовидные структуры :

а)О-есть дерево (называемое пустым деревом);

б) если Т1 и Т2 - деревья, то есть дерево (нарисованное сверху вниз):

3. Функция факториал n! для неотрицательных целых чисел :

а) 0!=1;

б) если n>0, то n! = n(n-1)!.

Мощность рекурсии связана с тем, что она позволяет определять бесконечное множество объектов с помощью конечного высказывания. Точно так же бесконечные вычисления можно описать с помощью конечной рекурсивной программы, даже если эта программа не содержит явных циклов. Однако лучше всего использовать рекурсивные алгоритмы в тех случаях, когда решаемая задача, или вычисляемая функция, или обрабатываемая структура данных определена с помощью рекурсии. В общем виде рекурсивную программу P можно изобразить как композицию R базовых операторов S_i(не содержащих P) и самой P:

PR [Si, P]. (4.1)

Необходимое и достаточное средство для рекурсивного представления программ - это описание процедур, или подпрограмм, так как оно позволяет присваивать какому-либо оператору имя, с помощью которого можно вызывать этот оператор.

С процедурой принято связывать некоторое множество локальных объектов, т.е. переменных, констант, типов и процедур, которые определены только в этой процедуре, а вне ее не существуют или не имеют смысла. Каждый раз, когда такая процедура рекурсивно вызывается, для нее создается новое множество локальных переменных. Хотя они имеют те же имена, что и соответствующие элементы множества локальных переменных, созданного при предыдущем обращении к этой процедуре, их значения различны. Следующие правила области действия идентификаторов позволяют исключить какой-либо конфликт при использовании имен: идентификаторы всегда ссылаются на множество переменных, созданное последним; то же правило относится и к параметрам процедуры.

В качестве примера рекурсивного алгоритма рассмотрим процедуру прохождения двоичного дерева во внутреннем порядке с присвоением узлам соответствующего номера.

Алгоритм 4.1.Нумерация узлов двоичного дерева в соответствии с внутренним порядком (INOR - INternal ORder).

ВХОД. Двоичное дерево, представленное массивами LES(LEFT Son-левый сын) и RIS(RIght Son-правый сын).

ВЫХОД. Массив, называемый NUM (NUMber - номер), такой, что NUM[i] - номер узла i во внутреннем порядке.

МЕТОД. Кроме массивов LES, RIS и NUM, алгоритм использует глобальную переменную COT (COunT-счет), значение которой - номер очередного узла в соответствии с внутренним порядком. Начальное значение переменной СОТ является 1. Параметр ND (NoDe-узел) вначале равен RT (RooT - корень). Процедура, изображенная на рис.4.1, применяется рекурсивно.

Сам алгоритм таков :

begin

COT  1;

INOR (RT);

end

Рекурсия дает несколько преимуществ и прежде всего простоту программ. Если бы приведенный выше алгоритм не был записан рекурсивно, надо было бы строить явный механизм для прохождения дерева. Двигаться вниз по дереву нетрудно, но чтобы обеспечить возможность вернуться к предку, надо запомнить всех предков в стеке, а операторы работы со стеком усложнили бы алгоритм.

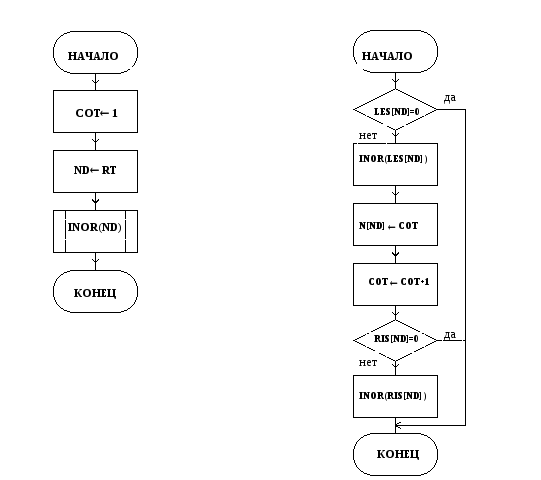
а) б)

Рис.4.1. СА с рекурсией для внутреннего порядка:

а - собственно алгоритм; б - процедура INOR.

procedure INOR (ND)

begin

if LES[ND]  0 then INOR (LES[ND]);

NUM[ND]  COT;

COT  COT + 1;

if RIS[ND]  0 then INOR (RIS[ND])

end

Рассмотрим возможный вариант того же алгоритма, но без использования рекурсии.

Алгоритм 4.2. Вариант алгоритма 4.1. без рекурсии.

ВХОД. Тот же, что и у алгоритма 4.1.

ВЫХОД. Тот же, что и у алгоритма 4.1.

МЕТОД. При прохождении дерева в стеке запоминаются все узлы, которые еще не были занумерованы и которые лежат на пути из корня в узел, рассматриваемый в данный момент. При переходе из узла v к его левому сыну узел v запоминается в стеке. После нахождения левого поддерева для v узел v нумеруется и выталкивается из стека. Затем нумеруется правое поддерево для v.

При переходе из v к его правому сыну узел v не помещается в стек, поскольку после нумерации правого поддерева мы не должны возвращаться в v, а должны вернуться к тому предку узла v, который еще не занумерован (т.е. к ближайшему предку w узла v такому, что v лежит в левом поддереве для w). Этот алгоритм приведен на рис. 4.2.

begin

COT  1 ;

ND  RT;

STK  0 ;

L : while LES[ND]  0 do

begin

PUSH; (* затолкнуть узел в стек *)

ND  LES[ND]

end;

C : NUM[ND]  COT;

COT  COT +1;

if RIS[ND]  0 then

begin

ND  RIS[ND];

goto L;

end;

if STK  0 then

begin

ND  ETS; (* ETS - номер элемента в вершине стека *)

POP; (* вытолкнуть узел из стека *)

goto C;

end

end.

Примечание:

L - Left;

C - Center.

`

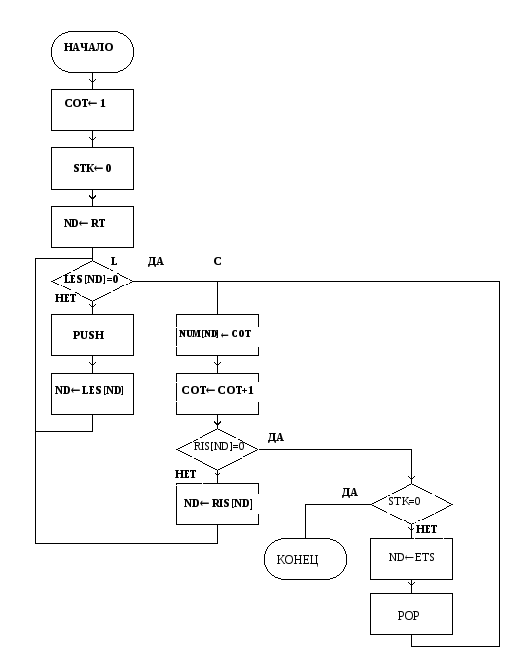
Рис.4.2. СА без рекурсии для внутреннего порядка

Подобно операторам цикла, рекурсивные процедуры могут привести к бесконечным вычислениям. Поэтому необходимо рас смотреть проблему окончания работы процедур. Очевидно, что для того, чтобы работа когда-либо завершилась, необходимо, чтобы рекурсивное обращение к процедуре Р подчинялось условию В, которое в какой-то момент времени перестает выполняться. Поэтому более точно схему рекурсивных алгоритмов можно представить так :

P  if B then R [Si, P] (4.2)

или

P  R [Si,if B then P]. (4.3)

Наиболее надежный способ обеспечить окончание процедуры - связать с Р параметр (значение) n и рекурсивно вызвать Р со значением этого параметра n-1. Тогда замена условия В на n>0 гарантирует окончание работы. Это можно изобразить следующими схемами программ:

P(n)  if n>0 then R [S_iiP(n-1)], (4.4)

P(n)  R [S_i,if n>0 then P(n-1)]. (4.5)

На практике нужно обязательно убедиться, что наибольшая глубина рекурсии не только конечна, но и не слишком велика. Дело в том, что при каждом рекурсивном вызове процедуры Р выделяется некоторая память для размещения ее переменных. Кроме этих локальных переменных, нужно еще сохранять текущее состояние вычислений, чтобы вернуться к нему, когда закончится выполнение новой активации Р и нужно будет вернуться к старой.

Рекурсивные алгоритмы наиболее пригодны в случаях, когда поставленная задача или используемые данные определены рекурсивно. Но это не значит, что при наличии таких рекурсивных определений лучшим способом решения задачи непременно является рекурсивный алгоритм.

Программы, в которых следует избегать использования рекурсии, можно охарактеризовать следующей схемой, изображающей их строение :

P  if B then (S; P) (4.6) или эквивалентной ей

P  (S; if B then P). (4.7)

Эти схемы естественно применять в тех случаях, когда вычисляемые значения определяются с помощью простых рекуррентных соотношений. Рассмотрим, например, широко известный пример вычисления факториалов f_i = i! :

i = 0, 1, 2, 3, 4, 5,... ,

f = 1, 1, 2, 6, 24, 120,... (4.8)

"Нулевое" число определяется явным образом как f₀=1, а последующие числа обычно определяются рекурсивно - с по- мощью предшествующего значения :

f_(i+1)=(i+1)·f_i (4.9)

Эта формула предполагает использование рекурсивного алгоритма для вычисления n-го факториального числа. Если мы введем две переменные I и F для значений i и f_i на i-м уровне рекурсии, то увидим, что для перехода к следующему числу в последовательности (4.8) необходимы следующие вычисления :

I  I+1; F  I*F (4.10) и, подставив (4.10) вместо S в (4.6), мы получим рекурсивную программу

P  if I<n then (I  I+1; F  F+1; P)

I  0; F  1; P (4.11)

Первую строку в (4.11) можно записать следующим образом

procedure P;

begin

if I<n then

begin

I  I+1; F  F*I; P

end

end (4.12)

Вместо процедуры можно ввести чаще используемую процедуру-функцию, т.е. некоторую процедуру, с которой явно связывается вычисляемое значение. Поэтому функцию можно использовать непосредственно как элемент выражения. Тем самым переменная F становится излишней, а роль I выполняет явный параметр процедуры.

function F(I);

begin

if I>0 then F  I*F(I-1)

else F  1

end (4.13)

Совершенно ясно, что здесь рекурсию можно заменить обычной итерацией, а именно программой

I  0; F  1;

while I<n do

begin

I  I+1; F  I*F

end (4.14)

В общем виде программы, соответствующие схемам (4.6) или (4.7), нужно преобразовать так, чтобы они соответствовали схеме

P  (x  xo; while B do S). (4.15)

Есть и другие, более сложные рекурсивные схемы, которые можно и должно переводить в итеративную форму. Примером служит вычисление чисел Фибоначчи, определяемых с помощью рекуррентного соотношения

fib_n+1 = fib_n + fib_n-1 для n>0 (4.16) и fib₁=1, fib₀=0.

При непосредственном подходе мы получим программу

function Fib(n);

begin

if n=0 then Fib(n)  0 else

if n=1 then Fib(n)  1 else

Fib  Fib(n-1) + Fib(n-2)

end (4.17)

При вычислении fib(n) обращение к функции Fib(n) приводит к рекурсивным активациям этой процедуры. Сколько раз? Мы можем заметить, что каждое обращение при n>1 приводит к двум дальнейшим обращениям, т.е. общее число обращений растет экспоненциально. Ясно, что такая программа непригодна для практического использования.

Однако очевидно, что числа Фибоначчи можно вычислить по итеративной схеме, при которой использование вспомогательных переменных x=fib_i и y=fib_i+1 позволяет избежать повторного вычисления одних и тех же значений :

/* вычисляем x=fib_n для n>0 */

i  0; x  1; y  0;

while i<n do

begin

z  x; i  i+1;

x x+y; y  z

end

Отметим, что три присваивания x, y и z можно выразить всего лишь двумя присваиваниями без использования вспомогательной переменной z : x  x+y; y  x-y.

Итак, вывод таков: следует избегать рекурсии, когда имеется очевидное итеративное решение поставленной задачи.

Но это не означает, что всегда нужно избавляться от рекурсии любой ценой. Во многих случаях она вполне применима, как будет показано при последующем изложении. Тот факт, что рекурсивные процедуры можно реализовать на нерекурсивных по сути машинах, говорит о том, что для практических целей любую рекурсивную программу можно преобразовать в чисто итеративную. Но это требует явного манипулирования со стеком рекурсий, и эти операции до такой степени заслоняют суть программы, что понять ее становится очень трудно. Следовательно, алгоритмы, которые по своей сути скорее рекурсивны, чем итеративны, нужно представлять в виде рекурсивных процедур.

Примеры рекурсивных процедур [Н.Вирт] - построение кривых Гильберта, Серпинского, алгоритмы с возвратом (задачи из области "искусственного интеллекта": покрыть всю доску nxn ходами коня; расстановка восьми ферзей на шахматной доске без взаимных угроз; задача об устойчивых браках).

Алгоритмы с возвратом

Особенно интересный раздел программирования - это задачи из области “искусственного интеллекта”. Здесь нужно строить алгоритмы, которые находят решение определенной задачи не по фиксированным правилам вычисления, а методом проб и ошибок. Обычно процесс проб и ошибок разделяется на отдельные подзадачи. Часто эти подзадачи наиболее естественно описываются с помощью рекурсии. Процесс проб и ошибок можно рассматривать в общем виде как процесс поиска, который постепенно строит и просматривает (а также обрезает) дерево подзадач. Во многих случаях такие деревья поиска растут очень быстро, обычно экспоненциально, в зависимости от заданного параметра. Соответственно увеличивается стоимость поиска. Часто дерево поиска можно обрезать, используя только эвристические соображения, и тем самым сводить количество вычислений к разумным пределам.

Далее на примере задачи о ходе коня рассматривается общий принцип разбиения таких подзадач на подзадачи и использование в них рекурсии.

Задача “Обход конем шахматной доски n x n”. Конь помещается на поле с начальными координатами Х₀, У₀. Нужно покрыть ходами коня всю доску (осуществить обход доски) за n²-1 ход , при том, что каждая поле посещается ровно один раз.

Эта задача покрытия n² полей сводится к более простой: или выполнить очередной ход, или установить, что никакой ход невозможен.

Характерная черта этого алгоритма состоит в том, что он предпринимает какие-то шаги по направлению к общему решению, эти шаги фиксируются (записываются), но можно возвращаться обратно и стирать записи, если оказывается, что шаг не приводит к решению, а заводит в “тупик”. Такое действие называется возвратом.

Пусть число возможных дальнейших путей на каждом шаге конечно и фиксировано (скажем, равно m); пусть используется явный параметр уровня, обозначающий глубину рекурсии и допускающий простое условие окончания. Тогда схема, типичная для задач подобного рода, может быть представлена следующим образом:

procedure try (i)

begin k  0; (* инициировать выборку возможных шагов*)

repeat k  k+1; выбрать k-й возможный путь;

if приемлемо then

begin записать его;

if i< n then (* решение неполно*)

begin try (I+1); (*попробовать очередной шаг*)

if неудачно then стереть запись

end

end

until удачно  (k=m)

end.

Алгоритмы нумерации узлов дерева в соответствии

с внутренним порядком

1. Алгоритм с использованием рекурсии

PROCEDURE INOR (ND)

begin

1. if LES[ND]0 then;

2. NUM[ND]  COT;

3. COT  COT+1

4. if RIS[ND]0 then INOR (RIS[ND])

end

2. Алгоритм без использования рекурсии ( но с использованием

стека)

PROCEDURE INOR (ND)

begin

COT  1

ND  RT

STK  0

L (left): while LES[ND]0 do

begin

PUSH ( *затолкнуть узел в стек* )

ND  LES[ND]

end;

C(centre): NUM[ND]  COT;

COT  COT+1;

if RIS[ND]0 then

begin

ND  RIS[ND]

goto L

end

if STK0 then

begin

ND  ETS ( * присвоить узлу номер элемента, находящегося в вершине стека*)

POP ( *вытолкнуть узел из стека*)

goto C

end

end

NUM (NUMber - номер) - массив, такой, что NUM[i] - номер узла во внутреннем порядке

COT (COunt - счет ) глобальная переменная с начальным значением 1

ND (NoDe - узел) - параметр, вначале равный корню RT (RooT)

INOR - internal order - внутренний порядок

STK - стек ( STacK)

ETS - элемент в вершине стека ( Element in the top of Stack)

МАТЕМАТИЧЕСКАЯ МУДРОСТЬ : Общего вида задачу решать проще, чем частную задачу!

[Пойа]

Рассмотрим процедуру INOR из алгоритма 4.1. Когда, например, она вызывает себя с фактическим параметром LES[ND], она запоминает в стеке адрес нового значения параметра ND вместе с адресом возврата, который указывает, что по окончании работы этого вызова выполнение программы продолжается со строки 2. Таким образом, переменная ND эффективно заменяется на LES[ND], где бы не входил ND в это определение процедуры.

В алгоритме 4.2. сделано так, что окончание выполнения вызова INOR с фактическим параметром RIS[ND] завершает выполнение и самой вызывающей процедуры. Поэтому нам не обязательно теперь хранить адрес возврата или узел(ND) в стеке если фактическим параметром является RIS[ND].