
1.3.4. Деревья и их представление
Конечное корневоедерево T формально определяется как непустое множество упорядоченных узлов, таких что существует один выделенный узел, называемыйкорнемдерева, а оставшиеся узлы разбиты на m>=0 поддеревьев Т1,Т2,...,Тm. Узлы, не имеющие поддеревьев, называютсялистьями; остальные узлы называются внутренними узлами.

Рис.3.8. Дерево с 11 узлами, помеченными буквами от А до К. Узлы с метками D,E,F,H,J и K являются листьями; другие узлы внутренние. Узел А - корень.
Посредством деревьев изображаются иерархические организации, поэтому они являются нелинейными структурами данных в комбинаторных алгоритмах.
В описанных соотношениях между узлами дерева мы используем терминологию, принятую в генеалогических деревьях. Так, мы говорим, что в дереве (или поддереве) все узлы являются потомками его корня, и наоборот, корень - предок всех своих потомков. Корень именуется отцом корней его поддеревьев, которые в свою очередь будут сыновьями корня. Например, на рис. 3.8 узел А является отцом узлов B,G и I; J и K - сыновья I, а C, E, F -братья.
Все рассматриваемые нами деревья будут упорядочены, т.е. для них будет важен относительный порядок расположения каждого узла. Таким образом, деревья считаются различными.
Определим лес как упорядоченное множество деревьев; в связи с этим мы можем перефразировать определение дерева: дерево есть непустое множество узлов, такое, что существует один выделенный узел, называемый корнем дерева, а оставшиеся узлы образуют лес с m>=0 поддеревьями корня.
Важной разновидностью корневых деревьев является класс бинарных деревьев. Бинарное дерево Т либо пустое, либо состоит из выделенного узла, называемого корнем, и двух бинарных поддеревьев: левого Тlи правого Tr. Бинарные деревья, вообще говоря не являются подмножеством множества деревьев, они полностью отличаются по своей структуре, поскольку две следующие картинки ( а) и б)) не изображают одно и то же бинарное дерево. Как деревья, однако, они обе неотличимы от ( в) ).
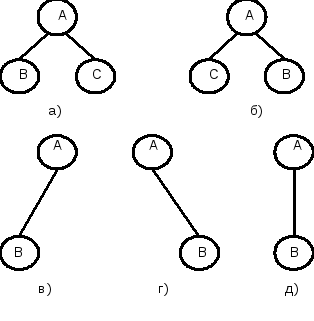
Рис.3.9 Фрагменты деревьев.
Различие между деревом и бинарным деревом состоит в том, что дерево не может быть пустым, и каждый узел дерева может иметь произвольное число поддеревьев; в тоже время бинарное дерево может быть пустым, каждая из его вершин может иметь 0, 1 или 2 поддерева, и существует различие между левыми и правыми поддеревьями.
Почти все машинное представления деревьев основаны на связанных распределениях. Каждый узел состоит из поля INFO и некоторых полей для указателей. Например, одно из представлений для каждого узла имеет единственное поле для указателя F (FATHER), указывающее на отца данного узла. При этом приведенное на рис.3.8 дерево будет выглядеть так, как показано на рис.310.

Рис.3.10.Дерево из рис.3.8, представленное из узлов с полем INFO и указателем FATHER.
Такое представление полезно, если необходимо подниматься по дереву от потомков к предкам. Такая операция встречается довольно редко; чаще требуется опуститься по дереву от предков к потомкам.
Представление дерева (или леса) с использованием указателей, ведущих от предков к потомкам, довольно сложно, поскольку узел, имея не более одного отца, может иметь в тоже время произвольно много сыновей. Другими словами, при таком представлении узлы должны различаться по размеру, что является определенным неудобством. Один из путей обхода этой трудности состоит в том, чтобы определить соотношение между деревьями и бинарными деревьями, поскольку бинарные деревья легко представить узлами фиксированного размера. Каждый узел в этом случае имеет три поля: LEFT (указывает положение корня левого поддерева), INFO (содержимое узла) и RIGHT (указатель местоположения корня правого поддерева). Все сказанное выше проиллюстри-ровано на рис.3.11.
 а)
б)
а)
б)
Рис.3.11. Бинарное дерево (а) и его представление (б) с помощью узлов с тремя
полями LEFT , INFO и RIGTH.
Мы можем представлять деревья как бинарные деревья ( используя узлы фиксированного размера), представляя каждый узел леса в виде узла, состоящего из полей LEFT, INFO и RIGHT. При этом поле LEFT предназначается для указания самого левого сына
данного узла, а поле RIGHT - для указания следующего брата данного узла. Например, лес (рис.3.11,а) преобразуется в бинарное дерево ( рис.3.11,б). Таким образом, мы используем поле LEFT некоторого узла для указателя на связанный список сыновей этого узла; этот список связывается с помощью полей RIGHT. Такое представление мы будем называть естественным соответствием между лесами и бинарными деревьями.
 а)
а)

Рис.3.12. Лес (а) и его представление в виде бинарного дерева (б)
Двоичное дерево обычно представляют в виде двух массивов LES (LEFTSON-левый сын) и RIS (RIGHTSON-правый сын). Пусть узлы двоичного дерева занумерованы целыми числами от 1 до N. В этом случае LES[i]=j <=> узел с номером j является левым сыном узла с номером i. Если у узла i нет левого сына, то LES[i]=0. RES[i] определяется аналогично.

а)
|
|
LES |
RIS |
|
1 |
2 |
6 |
|
2 |
3 |
4 |
|
3 |
0 |
0 |
|
4 |
0 |
5 |
|
5 |
0 |
0 |
|
6 |
7 |
8 |
|
7 |
0 |
0 |
|
8 |
0 |
9 |
|
9 |
0 |
0 |
Рис.3.13. Двоичное дерево (а) и его представление (б).
б)
Определение. Двоичное дерево называется полным, если для некоторого целого k каждый узел глубины меньше k имеет как левого, так и правого сына и каждый узел глубины k является листом. Полное двоичное дерево высоты k имеет ровно 2 -1 узлов.

Глубина узла v в дереве - это длина пути из корня в v.
Высота узла в дереве - это длина самого длинного пути из v в
какой-нибудь лист.
Высотой дерева называется высота его корня.
Уровень узла v в дереве равен разности высоты дерева и
глубины узла v. Например, на рис. хх4. узел 3 имеет глубину
2, высоту 0, и уровень 1.
Полное двоичное дерево высоты k часто представляют одним массивом. В позиции 1 этого массива находится корень. Левый сын узла в позиции i расположен в позиции 2i, а его правый сын - в позиции [i/2].
Во многих алгоритмах, построенных на деревьях, решается задача нахождения корня дерева ( посещением каждого его узла ) в некотором порядке. Известно несколько систематических способов сделать это. Мы рассмотрим три широко распространенных способа:
прохождение дерева в прямом порядке, обратном порядке и внутреннем порядке.
Определение. Пусть Т-дерево м корнем r и сыновьями v1, vk, k>=0. При k=0 это дерево состоит из единственного узла r.
Прохождение дерева в прямом порядке определяется следующей рекурсией:
1) посетить корень r,
2) посетить в прямом порядке поддеревья с корнями v1,...,vk в указанной последовательности.
Прохождение дерева в обратном порядке определяется следующей рекурсией:
1) посетить в обратном порядке поддеревья с корнями v1,...,vk в указанной последовательности,
2) посетить корень r.
Прохождение дерева во внутреннем порядке определяется следующей рекурсией:
1) посетить во внутреннем порядке левое поддерево корня(если оно существует),
2) посетить корень,
1) посетить во внутреннем порядке правое поддерево корня(если оно существует).
Пример. На рис.3.14. изображено двоичное дерево, узлы которого пронумерованы в соответствии с прохождением его различным образом.

Рис.3.14. Прохождение дерева: а) в прямом порядке; б) в обратном порядке; в) во внутреннем порядке.
Если при некотором прохождении дерева его узлам были присвоены некоторые номера, то на узлы удобно ссылаться по этим номерам. Так, v будет обозначать узел, которому был присвоен номер v. Если все узлы занумерованы в порядке посещения, то
рассмотренные нумерации обладают рядом интересных свойств.
При нумерации в прямом порядке все узлы поддерева с корнем r имеют номера, не меньшие r. Точнее, если Dr- множество потомков узла r, то v будет номером некоторого узла из Dr<=> r<=v<r+| Dr|. Поставив в соответствие каждому узлу его номер в прямом порядке и количество его потомков, легко определить, является ли некоторый узел w потомком для v. После того, как номера присвоены (в соответствии с прямым порядком) и вычислено количество потомков каждого узла, можно определить, является ли w потомком для v, причем за фиксированное время, не зависящее от размера дерева. Номера, соответствующие обратному порядку, обладают аналогичными свойствами.
Номера узлов дерева, соответствующие внутреннему порядку, обладают тем свойством, что номера узлов в левом поддереве для v меньше v, а в правом поддереве больше v. Таким образом, чтобы найти узел с номером w, надо сравнить w с корнем r. Если w=r, то искомый узел найден. Если w<r, то повторить этот процесс для левого поддерева; усли w>r, то повторить процесс для правого поддерева. В конце концов узел с номером w будет найден.
Определение. Неориентированным деревом называется неориентированный ациклический связный (любые два узла соединены путем) граф. Корневое неориентированное дерево - это неориентированное дерево, в котором узел выделен в качестве корня.
Ориентированное дерево можно превратить в корневое неориентированное, просто сделав все его ребра неориентированными. Мы будем употреблять одну и ту же терминологию и пользоваться одними и теми же обозначениями для корневых неориентированных и для ориентированных деревьев. Основное математическое различие здесь состоит в том, что все пути в ориентированном дереве идут от предков к потомкам, тогда как в корневом неориентированном дереве пути могут идти в обоих направлениях.
