TA / 2.3.2 Модели вычислений(продолжение)

Глава 2. Модели вычислений

2.3.2. Машина Тьюринга, её свойства и особенности

Раньше были отмечены интуитивно очевидные требования к алгоритмам: детерминированность, массовость и направленность. При этом не важно, как алгоритм реализуется: человеком или машиной. Из отличительных свойств алгоритмов вытекают общие требования к машине, выполняющей алгоритм:

1. Машина должна быть полностью детерминированной и действовать в соответствии с заданной системой правил.

2. Машина должна допускать ввод различных начальных данных, соответствующих различным задачам из заданного класса задач.

3. Заданная система правил работы машины и класс решаемых задач согласованы так, чтобы всегда можно было "прочитать" результат работы машины.

Можно предложить различные конструкции машин, способных выполнять алгоритмы. Наиболее наглядная конструкция была предложена английским математиком Тьюрингом (рис. 2.4а).

Машина содержит бесконечную одномерную ленту, которая разделена на ячейки. Будем считать, что лента бесконечна лишь в одном направлении (вправо), так что существует ячейка, про которую можно сказать, что она нулевая (самая левая). В каждой ячейке может быть записан лишь один символ Xi из конечного алфавита X={Xо,...,Xn}; символ Хо мы выделяем специально и будем говорить, что если в некоторой ячейке записан символ Хо, то эта ячейка "пустая". В дальнейшем будем считать, что непустых символов на ленте каждый раз имеется конечное (но сколь угодно большое) число, остальные ячейки - пустые.

В конструкцию МТ входит также специальное устройство, содержащее считывающую и записывающую головку (далее - просто головка), которая может располагаться над любой из ячеек ленты и по команде из вне может "стереть" записанный в этой ячейке символ и записать новый. Головка может также по команде перемещаться на одну позицию вправо или влево (если она не находится в самой левой ячейке). Команды на головку подаются от управляющего устройства (УУ), которое в свою очередь получает от головки сигнал о наличии того или иного символа в ячейке ленты, расположенной под головкой.

УУ имеет конечное число состояний ( m + 1 ) из множества Q={q0,q1,.,qm} и работает в дискретном времени t = 0,1,2.

Входные данные для УУ: символ Хi, считываемый головкой с текущей ячейки с номером l.

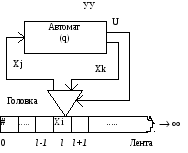
Рис 2.4а Машина Тьюринга, конструкция

Выходные данные УУ: а также команда управления перемещения головки {L, R, S} (L- влево, R- вправо, S - не перемещается), символ Хк который головка должна записать в ячейку .

Пусть в момент времени t головка находилась напротив второй ячейки l, в которой был записан символ Хi, а управляющее устройство находилось в состоянии qj . УУ в зависимости от пары символов (qj, Хi) выдает символ Хk (т.е. головка стирает старый символ Хi и записывает новый символ Хk ), а затем один из символов R, L, S, в соответствии с которым головка перемещается. После этого УУ переходит в новое состояние qr (также однозначно определенное парой символов (qj, Xi) ). Тем самым в момент t+1 в l-ой ячейке будет записан символ Xk, УУ будет находиться в состоянии qr, а головка может находиться напротив l+1, l-1 или l-ой ячейки.

Важно запомнить, что МТ работает последовательно (т.е. последовательно, ячейку за ячейкой обрабатывает данные в зависимости от команд)

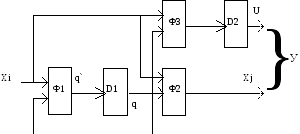
Рис 2.4.б Машина Тьюринга, структура

Таблица 2.3

МТ	Xo	...	Xi	...	Xn
qo	qoXoS	...	qoXiS	...	qoXnS
...	...	...	...	...	...
qj	qoXoL	...	qrXkS	...	qjXiR
...	...	...	...	...	...

Если функциональная схема МТ задана, то при каждом заполнении ленты работа машины однозначно определена.

Далее будем считать, что символ qо состояния УУ означает состояние покоя МТ, т.е. строка qо функциональной схемы обладает следующими свойствами:

- первым символом в каждой клетке этой строки всегда является qо.

- вторым символом в клетке столбца Хi этой строки является символ Хi.

- третьим символом в каждой клетке строки является символ S.

Поэтому, если УУ в какой-то момент времени имеет состояние qо, то где бы не находилась головка и каким бы ни было запоминание ленты, в последний момент времени УУ будет оставаться в том же состоянии, заполнение ленты остается прежним, головка также не сдвинется. Для упрощения записи ФС мы будем опускать в ней строку qо.

В дальнейшем для простоты будем предполагать, что алфавит символов {Хi} состоит из двух символов: "пустого" -0 и "не пустого" - 1.

Рассмотрим несколько примеров МТ.

Начальным состоянием машины здесь и далее будем считать состояние q1. Все рассмотренные в этих примерах машины имеют по одному состоянию (не считая состояния покоя).

Пример 2.4. Машина А (табл. 2.4)

Если в начальный момент времени машина воспринимает заполненную ячейку, то она "отыскивает" на ленте первую пустую (т.е. заполненную символом 0 ячейку) справа от той, под которой находится головка, печатает там символ 1 и останавливается. Если вначале головка находится напротив пустой ячейки, то машина ее "заполняет" и останавливается, не передвигая головку.

Пример 2.5. Машина B (табл. 2.5)

Она "стирает" единицу в той ячейке, над которой находится головка (если ячейка не пустая), передвигается влево и останавливается .Если в начальный момент ячейка под головкой пустая, то головка передвигается влево до тех пор, пока не найдет заполненную ячейку, стирает там единицу, передвигает головку влево и останавливается.

Пример 2.6. Машина С (табл. 2.6).

Машина отправляясь от заполненной ячейки, идет влево и останавливается левее группы единиц на две ячейки.

Пример 2.7. Машина D (табл. 2.7)

Машина, имея два состояния покоя, распознает напротив какой ячейки находится - пустой либо заполненной; в зависимости от этого переходит в первое либо второе состояние покоя.

Пример 2.8. Композиция N (табл. 2.8). ФС для N

Таблица 2.4 Таблица 2.5 Таблица 2.6 Таблица 2.7

A

0

1

B

0

1

C

0

1

D

0

1

q1

qo1S

q11R

q1

q10L

q00L

q1

q00L

q11L

q1

q`00S

q``01S

В некоторых случаях МТ может быть недоопределена в том смысле, что не все ячейки её функциональной схемы (ФС) заполнены. Это допускается в тех случаях, когда по тем или иным причинам можно заранее сказать, что соответствующие сочетания состояний машины и символов по ленте никогда не встречаются.

Иногда машина может иметь несколько состояний покоя (q0', q0'', q0```...).

Суперпозиция машин Тьюринга.

Относительно МТ применимы следующие соглашения:

1) работа МТ однозначно определена функционированием УУ в соответствии с функциональной схемой;

2) МТ начинает работу от начального состояния, обозначаемого символом q₁, и всегда имеет состояние покоя q₀, которым заканчивается её работа.

Такие соотношения позволяют определить операции над МТ, благодаря которым можно по заданным ФС можно получать новые ФС.

Различают следующие виды суперпозиций: композиция (произведение) и итерация, а также их комбинации.

Пусть имеются две МТ, T₁ и T₂. Произведением МТ T₁ и T₂ называется машина T, ФС которой строится следующим образом:

- если УУ машин T₁ и T₂ имеют m₁ и m₂ состояний соответственно (исключая состояние покоя), то УУ машины T имеет m₁+m₂ состояний, причём начальным состоянием машины T является начальное состояние машины T₁(q₁=q₁¹), а конечным - состояние покоя машины T₂(q₀=q₀²), то есть машина T₁ начинает работу, затем передает »эстафету управления» машине T₂ , а T₂ заканчивает её;

- ФС машины T состоит из двух частей: верхняя описывает машину T₁, а нижняя - машину T₂, причём состояние покоя T₁ отождествляется с начальным состоянием T₂, то есть q₀¹=q₁².

Операция умножения машин обладает свойствами:

1) T₁T₂ T₂T₁ (некоммутативность);

2) (T₁T₂)T₃=T₁(T₂T₃)=T₁T₂T₃ (ассоциативность).

Возможен случай произведения одинаковых машин - степень МТ:

Tⁿ=TT... T, n - раз.

До сих пор речь шла об умножении машин, имеющих одно состояние покоя. В том случае, когда одна из перемножаемых машин имеет несколько состояний покоя, умножение определяется аналогично (...), но обязательно должно присутствовать указание, какое из состояний покоя предыдущего сомножителя отождествляется с начальным состоянием данного. Так, например, если машина T₁ имеет два состояния покоя, то произведение T₁ и T₂ мы будем обозначать через

T=T₁ либо T=T₁

в зависимости от того, отождествляется ли начальное состояние машины T₂ с первым либо со вторым состоянием покоя машины T₁. Машина T в этом случае также имеет два состояния покоя: для первого варианта - состояние покоя машины T₂ либо второе состояние покоя машины T₁, для второго варианта - первое состояние покоя машины T₁ либо состояние покоя машины T₂.

Из предыдущего изложения ясен также смысл такой, например, записи (формулы):

T= T₁.

Здесь умножение производится независимо по двум “каналам”, связанным с первым либо вторым состояниями покоя машины T₁.

Рассмотрим операцию итерации, которая применяется к одной машине. Пусть машина T₁ имеет r состояний покоя. Выберем какое либо l-е состояние покоя и отождествим его в ФС машины T₁ с начальным состоянием. Полученная машина является результатом итерации машины T₁ и обозначается через

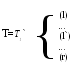
Здесь штрихи над T₁ и l указывают на отождествление l-го состояния покоя машины T₁ с её начальным состоянием. Отметим, что если T₁ имеет лишь одно состояние покоя, то после применения итерации получается машина, не имеющая вовсе состояния покоя.

Пример 2.7 Пусть имеются 4 машины (A, B, C и D), заданные своими ФС (табл. 2.4 - 2.7). Суперпозиция N из заданных МТ описывается формулой:

{

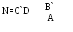Требуется определить для суперпозиции N следующее:

1) функциональную схему;

2) схему алгоритма;

3) словесное описание;

4) граф переходов.

1. Составляем для машины N функциональную схему, заполняя её строками из ФС каждой машины в том порядке, в каком они записаны в формуле (слева на право и сверху в низ); далее записываем состояния в первой колонке таблицы в порядке возрастания их номеров и в соответствии с этим проводим переобозначение состояний в двух других колонках с учетом правил передачи «эстафеты» управления. В результате получаем табл.2.8

Таблица 2.8

	N	0	1
C	q1	q20L	q11L
D	q2	q30S	q41S
B	q3	q30L	q10L
A	q4	q01S	q41R

2.По ФС строим схему алгоритма, исходя из того, что каждая строка ФС может рассматриваться как условный оператор программы функционирования МТ, а состояние - как метки этой программы. Рис. 2.5а демонстрирует СА функционирования машины N. Здесь SL(x) процедура поиска на ленте символа х (х={0,1}) при движении головки влево, R,L - перемещение головки на одну ячейку вправо или влево; Z - содержимое текущей ячейки.

3. По СА функционирования (это можно сделать и по ФС) сформируем один из вариантов словесного описания алгоритмов функционирования машины N:

машина, двигаясь влево, отыскивает одинокую пустую ячейку (ситуацию ...101... на ленте), заполняет её и останавливается над ней.

Отметим, что при отсутствии на ленте указанной ситуации головка дойдет до левой границы ленты.

4. В соответствии с табл.2.8 строим граф переходов машины N (рис. 2.5в), отмечая на переходах из состояния в состояние реакцию УУ (команды головке на запись символа в ячейке и на её перемещение) в зависимости от символа обозреваемого на ленте.

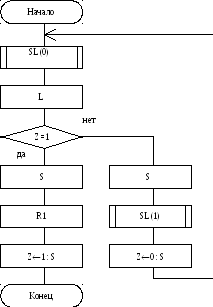
Рис 2.5 а Машина N, основная схема алгоритма.

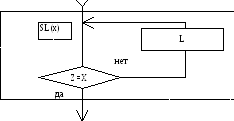
Рис 2.5 б Машина N, схема алгоритма для процедуры SL(x)

Рис 2.5 в Машина N, граф переходов.