3.Інструкція користувача
3.1 Сортування методом Шелла
У 1959 році Д.Л.Шелл запропонував
замість систематичного включення
елемента з індексом i в підмасив попередніх
йому елементів (цей спосіб суперечить
принципу "балансування", чому і не
дозволяє отримати ефективний алгоритм)
включати цей елемент в підсписок, що
містить елементи з індексами ih,
i-2h,
i-3h і
т.д., де h - деяка натуральна постійна.
Таким чином формується масив, в якому
h-серії елементів, віддалених один від
одного на відстань h, сортуються окремо:
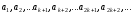
Після того, як розсортовані непересічні h-серії, процес поновлюється з новим значенням h '<h. Попереднє сортування серій з відстанню h значно прискорює сортування серій з відстанню h '.
Доведено, що максимальна складність алгоритму Шелла становить O (n5 / 4). Так як
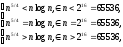 (3.1)
(3.1)
то цей вид сортування придатний для послідовностей, що мають приблизно до 70 тис. елементів.
3.1.1 Покращення
При виборі опорного елемента з даного діапазону випадковим чином гірший випадок стає дуже малоймовірним і очікуваний час виконання алгоритму сортування - O (n lg n).
Вибирати опорним елементом середній з трьох (першого, середнього і останнього елементів). Такий вибір також спрямований проти гіршого випадку.
Щоб уникнути досягнення небезпечної глибини рекурсії в гіршому випадку (або при наближенні до нього) можлива модифікація алгоритму, що усуває одну гілку рекурсії: замість того, щоб після поділу масиву викликати рекурсивну процедуру поділу для обох знайдених підмасива, рекурсивний виклик робиться тільки для меншого підмасива, а більший обробляється в циклі в межах цього ж виклику процедури. З точки зору ефективності в середньому разі різниці практично немає: накладні витрати на додатковий рекурсивний виклик і на організацію порівняння довжин підмасива і циклу - приблизно одного порядку. Зате глибина рекурсії ні за яких обставин не перевищить log2n, а в гіршому випадку виродженого поділу вона взагалі буде не більше 2 - вся обробка пройде в циклі першого рівня рекурсії.
Розбивати масив не на дві, а на три частини (див. Dual Pivot Quicksort).
3.1.2 Переваги:
Один з найбільш швидкодіючих (на практиці) з алгоритмів внутрішнього сортування загального призначення.
Простий в реалізації.
Потребує лише додаткової пам'яті для своєї роботи. (Не покращений рекурсивний алгоритм у гіршому випадку пам'яті)
Добре поєднується з механізмами кешування і віртуальної пам'яті.
Існує ефективна модифікація (алгоритм Седжвіка) для сортування рядків - спочатку порівняння з опорним елементом тільки за нульовим символу рядка, далі застосування аналогічної сортування для «більшого» і «меншого» масивів теж за нульовим символу, і для «рівного» масиву по вже першого символу .
3.1.3 Недоліки:
Сильно деградує за швидкістю
(до![]() )
при невдалих виборах опорних елементів,
що може трапитися при невдалих вхідних
даних. Цього можна уникнути, використовуючи
такі модифікації алгоритму, як Introsort,
або вероятностно, вибираючи опорний
елемент випадково, а не фіксованим
чином.
)
при невдалих виборах опорних елементів,
що може трапитися при невдалих вхідних
даних. Цього можна уникнути, використовуючи
такі модифікації алгоритму, як Introsort,
або вероятностно, вибираючи опорний
елемент випадково, а не фіксованим
чином.
Наївна реалізація алгоритму
може привести до помилки переповнення
стека, так як їй може знадобитися зробити
вкладених рекурсивних викликів. У
покращених реалізаціях, в яких рекурсивний
виклик відбувається тільки для сортування
меншою з двох частин масиву, глибина
рекурсії гарантовано не перевищить![]() .
.
Нестійкий - якщо потрібна стійкість, доводиться розширювати ключ.
Розглянемо роботу процедури для масиву a [0] ... a [6] і опорного елемента p = a [3].
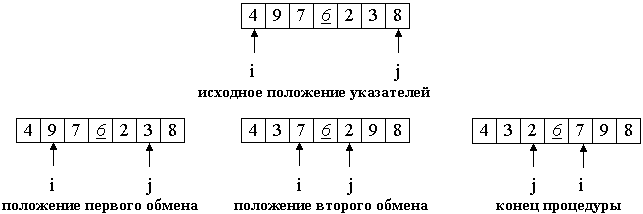
Рисунок 5.8 – Приклад роботи процедури сортування
3.2 Сортування вставками
У функцію InsertionSort передається масив A і довжина списку n. Розглянемо i-ий прохід (1 <i <n-1). Підсписок від A [0] до A [i-1] вже відсортований за зростанням. Як вставляється (TARGET) виберемо елемент A [i] і будемо просувати його до початку списку, порівнюючи з елементами A [i-1], A [i-2] і т.д. Перегляд закінчується на елементі A [j], який менше або дорівнює TARGET або знаходиться на початку списку (j = 0). У міру просування до початку списку кожний елемент зсувається вправо (A [j] = A [j-1]). Коли відповідне місце для A [i] буде знайдено, цей елемент вставляється в точку j.
Сортування вставками вимагає фіксованого числа проходів. На n-1 проходах вставляються елементи від A [1] до A [n-1]. На i-му проході вставки виробляються в підсписок A [0]-A [i] і вимагають в середньому i / 2 порівнянь. Загальне число порівнянь єдине:
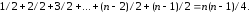 (3.2)
(3.2)
На відміну від інших методів, сортування вставками не використовує обміни. Складність алгоритму вимірюється числом порівнянь і дорівнює O (n2). Найкращий випадок - коли початковий список вже відсортований. Тоді на i-му проході вставка здійснюється в точці A [i], а загальне число порівнянь одно n-1, тобто складність становить O (n). Найгірший випадок виникає, коли список відсортований за спаданням. Тоді кожна вставка відбувається в точці A [0] і вимагає i порівнянь. Загальне число порівнянь одно n (n-1) / 2, тобто складність становить O (n2).
В принципі, алгоритм сортування вставками можна значно прискорити. Для цього слід не зрушувати елементи по одному, як це продемонстровано в наведеному вище прикладі, а знаходити потрібний елемент за допомогою бінарного пошуку, описаного в попередньому номері (тобто, в циклі розбиваючи список на дві рівні частини, поки в списку не залишиться один- два елементи), а для зсування використовувати функції копіювання пам'яті. Такий підхід дає досить високу продуктивність на невеликих масивах. Основним вузьким місцем у даному випадку є саме копіювання пам'яті. Поки що обсяг копійованих даних (близько половини розміру масиву) можна порівняти з розміром кеша процесора 1 рівня, продуктивність цього методу досить висока. Але через множинних непродуктивних повторів копіювання, цей спосіб менш кращий, ніж метод «швидкої» сортування, описаний в наступному розділі. Цей же метод можна рекомендувати у разі щодо статичного масиву, в який зрідка проводиться вставка одного-двох елементів.
3.3 Сортування вибором
Оцінимо часову складність даного методу, використовуючи в якості основної операції операцію порівняння.
Для пошуку мінімального елемента в кожному проході потрібно виконати: n-1, n-2, 1 операцій порівняння, тобто всього n (n-1) / 2 операцій порівняння. Отже, обчислювальна складність даного методу O (n2). Причому час сортування не залежить від вихідного порядку елементів.
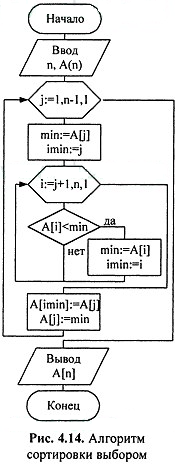
Рисунок 3.1 – Алгоритм сортування вибором
3.4 Метод швидкого сортування
Загальний аналіз ефективності «швидкої» сортування досить важкий. Буде краще показати її обчислювальну складність, підрахувавши число порівнянь при деяких ідеальних припущеннях. Припустимо, що n - ступінь двійки, n = 2k (k = log2n), а центральний елемент розташовується точно посередині кожного списку і розбиває його на два підсписки приблизно однакової довжини.
При першому скануванні проводиться n-1 порівнянь. В результаті створюються два підсписки розміром n / 2. На наступній фазі обробка кожного підсписки вимагає приблизно n / 2 порівнянь. Загальне число порівнянь на цій фазі дорівнює 2 (n / 2) = n. На наступній фазі обробляються чотири підсписки, що вимагає 4 (n / 4) порівнянь, і т.д. Зрештою процес розбиття припиняється після k проходів, коли вийшли підсписки містять по одному елементу. Загальне число порівнянь приблизно дорівнює n + 2 (n / 2) + 4 (n / 4) + ... + N (n / n) = n + n + ... + N = n * k = n * log2n
Для списку загального вигляду обчислювальна складність «швидкої» сортування дорівнює O (n log2 n). Ідеальний випадок, який ми тільки що розглянули, фактично виникає тоді, коли масив вже відсортований за зростанням. Тоді центральний елемент потрапляє точно в середину кожного підсписки.
Якщо масив відсортований за спаданням, то на першому проході центральний елемент виявляється на середині списку і змінюється місцями з кожним елементом як у першому, так і в другому підсписки. Результуючий список майже відсортований, алгоритм має складність порядку O (n log2n).(рис. 3.2.1)
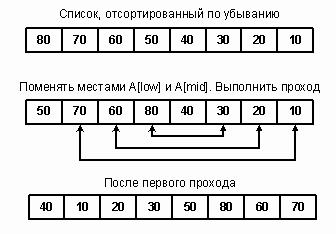
«Рисунок 3.2.1−опис методу швидкого сортування»
Найгіршим сценарієм для «швидкої» сортування буде той, при якому центральний елемент весь час потрапляє в одноелементні подспісок, а всі інші елементи залишаються в другому підсписки. Це відбувається тоді, коли центральним завжди є найменший елемент. Розглянемо послідовність 3, 8, 1, 5, 9.
На першому проході проводиться n порівнянь, а більший подспісок містить n-1 елементів. На наступному проході цей подспісок вимагає n-1 порівнянь і дає подспісок з n-2 елементів і т.д. Загальне число порівнянь одно: n + n-1 + n-2 + ... + 2 = n (n +1) / 2 - 1
Складність найгіршого випадку дорівнює O (n2), тобто не краще, ніж для сортувань вставками і вибором. Однак цей випадок є патологічним і малоймовірний на практиці. Загалом, середня продуктивність «швидкої» сортування вище, ніж у всіх розглянутих нами сортувань.
Алгоритм QuickSort вибирається за основу в більшості універсальних сортують утиліт. Якщо ви не можете змиритися з продуктивністю найгіршого випадку, використовуйте пірамідальну сортування - більш стійкий алгоритм, складність якого дорівнює O (n log2n) і залежить тільки від розміру списку.
3.4 Метод сортування бульбашкою
Алгоритм метод бульбашки - найбільш простий метод сортування масиву. через
своєї простоти цей метод не дуже ефективний і вимагає процесорного часу
більше, ніж інші методи. Однак для сортування невеликих масивів
використання методу бульбашки прийнятно. Припустимо, що масив сортується в
порядку зростання, тоді метод бульбашки використовує цикл за значеннями масиву,
переміщаючи поступово найбільше значення в кінець масиву (подібно до того, як в
воді спливає на поверхню пляшечку).
Сортування методом бульбашки займає 61,3 секунд.
ВИСНОВКИ
Отже, ми розглянули як працюють деякі алгоритми сортування і спробували визначити їх складність.
Застосування того чи іншого алгоритму сортування для вирішення конкретної задачі є досить складною проблемою, вирішення якої потребує не лише досконалого володіння саме цим алгоритмом, але й всебічного розглядання того чи іншого алгоритму, тобто визначення усіх його переваг і недоліків.
В даній курсовій роботі ми розглянули «елементарні» та більш складні, а точніше швидкі алгоритми сортування. Звичайно, необхідність застосування саме швидких алгоритмів сортування очевидна. Адже прості алгоритми сортування не дають бажаної ефективності в роботі програми. Але завжди треба пам’ятати й про те, що кожний швидкий алгоритм сортування поряд із своїми перевагами може містити і деякі недоліки.
В нашій роботі ми розглянули деякі алгоритми сортування та їх реалізацію мовою С++, дослідили не лише переваги таких алгоритмів, ефективність їх використання, але й визначили деякі недоліки окремих алгоритмів, що заважають вживати їх для вирішення першої ліпшої задачі сортування.
Отже, головною задачею, яку має вирішити людина, яка повинна розв’язати задачу сортування – це визначення як позитивних, так і усіх негативних характеристик різних алгоритмів сортування, передбачення кінцевого результату. До того ж , треба враховувати головне – чи , можливо, цю задачу задовольнить один з класичних простих алгоритмів сортування.
ПЕРЕЛІК ВИКОРИСТАНИХ ДЖЕРЕЛ
Страуструп Б. Язык программирования С++. Часть 2. — Киев: "ДиаСофт", 1993. — 296 с
Х.М.Дейтел, П.Дж. Дейтел Как программировать на С++.- М.:ЗАО «Издательство БИНОМ», 2000 г. — 1024 с.
Страуструп Б. Язык программирования С++. Часть 1. — Киев: "ДиаСофт", 1993. — 264 с.
Марченко А.Л. "C++. Бархатный путь" (избранные главы)
ДОДАТОК А
#include "stdafx.h"
#include <iostream>
#include <stdlib.h>
#include <time.h>
using namespace std;
template <class T>
void bubbleSort (T a [], long size) {
long i, j;
T x;
for (i = 0; i <size; i ++) {// i - номер проходу
for (j = size-1; j> i; j --) {// внутрішній цикл проходу
if (a [j-1]> a [j]) {
x = a [j-1]; a [j-1] = a [j]; a [j] = x; }}}}
template <class T>
void shakerSort (T a [], long size) {
long j, k = size-1;
long lb = 1, ub = size-1; // межі невідсортованої частини масиву
T x;
do {
// Прохід знизу вгору
for (j = ub; j> 0; j --) {
if (a [j-1]> a [j]) {
x = a [j-1]; a [j-1] = a [j]; a [j] = x;
k = j;}}
lb = k +1;
// Прохід зверху вниз
for (j = 1; j <= ub; j ++) {
if (a [j-1]> a [j]) {
x = a [j-1]; a [j-1] = a [j]; a [j] = x;
k = j;}}
ub = k-1;
} while (lb <ub);
};
int increment (long inc [], long size) {
int p1, p2, p3, s;
p1 = p2 = p3 = 1;
s = -1;
do {
if (++s % 2) {
inc [s] = 8 * p1 - 6 * p2 + 1;
} else {
inc [s] = 9 * p1 - 9 * p3 + 1;
p2 *= 2;
p3 *= 2;
}
p1 *= 2;
} while (3 * inc [s] <size);
return s > 0? -- s: 0;
};
template <class T>
void shellSort (T a [], long size) {
long inc, i, j, seq [40];
int s;
// Обчислення послідовності збільшень
s = increment (seq, size);
while (s >= 0) {
// Сортування вставками з інкрементом inc []
inc = seq [s --];
for (i = inc; i < size; i ++) {
T temp = a [i];
for (j = i - inc; (j >= 0) && (a [j] > temp); j -= inc)
a [j + inc] = a [j];
a [j + inc] = temp;
}
}
}
/*
int increment (long inc [], long size) {
// Inc [] масив, в які заносяться інкремент
// Size розмірність цього масиву
int p1, p2, p3, s;
p1 = p2 = p3 = 1;
s = -1;
do {// заповнюємо масив елементів за формулою Роберта Седжвіка
if (++ s% 2) {
inc [s] = 8 * p1 - 6 * p2 + 1;
} else {
inc [s] = 9 * p1 - 9 * p3 + 1;
p2 *= 2;
p3 *= 2;}
p1 *= 2;
// Заповнюємо масив, поки поточна інкремента хоча б в 3 рази менше кількості елементів у масиві
} while (3 * inc [s] < size);
return s > 0? - s: 0;
};// повертаємо кількість елементів у масиві
*/
/*
template <class T>
void shellSort (T a [], long size)
{
long inc, i, j, seq [40];
int s = increment (seq, size);
while (s> = 0) {
inc = seq [s -];
for (i = inc; i <size; i ++) {
T temp = a [i];
for (j = i-inc; (j> = 0) && (a [j]> temp); j - = inc)
a [j + inc] = a [j];
a [j + inc] = temp;
}
}
}
*/
template <class T>
void selectSort (T a [], long size) {
long i, j, k;
T x;
for (i = 0; i <size; i ++) {// i - номер поточного кроку
k = i; x = a [i];
for (j = i +1; j <size; j ++) // цикл вибору найменшого елемента
if (a [j] <x) {
k = j; x = a [j]; // k - індекс найменшого елемента
}
a [k] = a [i]; a [i] = x;}}
template <class T>
void insertSort (T a [], long size) {
T x;
long i, j;
for (i = 0; i <size; i ++) {// цикл проходів, i - номер проходу
x = a [i];
// Пошук місця елемента в готовій послідовності
for (j = i-1; j >= 0 && a [j]> x; j --)
a [j +1] = a [j]; // зрушуємо елемент направо, поки не дійшли
// Місце знайдено, вставити елемент
a [j +1] = x;}}
/*
template <class T>
inline void insertSortGuarded (T a [], long size) {
T x;
long i, j;
T backup = a [0]; // зберегти старий перший елемент
setMin (a [0]); // замінити на мінімальний
// Відсортувати масив
for (i = 1; i <size; i ++) {
x = a [i];
for (j = i-1; a [j]> x; j -)
a [j +1] = a [j];
a [j +1] = x;}
// Вставити backup на правильне місце
for (j = 1; j <size && a [j] <backup; j ++)
a [j-1] = a [j];
// Вставка елемента
a [j-1] = backup;}
*/
int main ()
{
int size;
cout << "Enter size: ";
cin >> size;
int * mass0 = new int [10];
int * mass1 = new int [10];
int * mass2 = new int [10];
int * mass3 = new int [10];
int * mass4 = new int [10];
srand (time (NULL));
for (int i = 0; i < 10; i ++)
mass0 [i] = mass1 [i] = mass2 [i] = mass3 [i] = mass4 [i] =rand () % 1000;
for (int i = 0; i < 10; i ++)
cout << mass0 [i] << ' ';
cout << endl << endl;
bubbleSort (mass0, 10);
shakerSort (mass1, 10);
shellSort (mass2, 10);
selectSort (mass3, 10);
insertSort (mass4, 10);
for (int i = 0; i < 10; i ++)
cout << mass0 [i] << ' ';
cout << endl << endl;
for (int i = 0; i < 10; i ++)
cout << mass1 [i] << ' ';
cout << endl << endl;
for (int i = 0; i < 10; i ++)
cout << mass2 [i] << ' ';
cout << endl << endl;
for (int i = 0; i <10; i ++)
cout << mass3 [i] << ' ';
cout << endl << endl;
for (int i = 0; i < 10; i ++)
cout << mass4 [i] << ' ';
cout << endl << endl;
delete [] mass0;
delete [] mass1;
delete [] mass2;
delete [] mass3;
delete [] mass4;
system ("pause");
return 0;
}
ДОДАТОК Б