Ответы к экзамену по дм

1).1. Полный граф — простой граф, в котором каждая пара различных вершин смежна.

2.Простой граф - граф, не имеющий петель и кратных рёбер

3. Дерево - граф связный и не имеет циклов.

4. Изоморфный граф :Граф называется изоморфным графу , если существует биекция из множества вершин графа в множество вершин графа

5. Двудо́льный граф —граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части.

6. Матрица смежности — это квадратная матрица A размера n, в которой значение элемента aij равно числу рёбер из i-й вершины графа в j-ю вершину.

7.прямое отображение - Прямым отображением 1-го порядка вершины хi является множество таких вершин графа, для которых существует дуга (хi, xj),

8. , которое называется обратным отображению f,

9. Матрица инцидентности —связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам. Ненулевое значение в ячейке матрицы указывает связь между вершиной и ребром

10. Степень вершины -вершины называется число инцидентных ей ребер.

11. Матрица достижимости— бинарная матрица замыкания по транзитивности отношения .В матрице достижимости хранится информация о существовании путей между вершинами орграфа.

12. Клика — полный подграф неориентированного графа.

13. Цикломатическое число графа — минимальное число ребер, которые надо удалить, чтобы граф стал ациклическим (деревом).

14.Центр графа-множество всех его центральных вершин.

15. Диаметр графа — это максимальное из расстояний между парами его вершин.

16. Радиус графа — минимальный из эксцентриситетов вершин связного графа

17. Мост - ребро графа, удаление которого увеличивает число компонент.

18. Независимое множество вершин - есть множество вершин графа G, такое, что любые две вершины в нем не смежны .

19.Плоский граф – граф,который можно уложить на плоскость без скрещивания рёбер.

20. Хроматическое число— минимальное число цветов, в которые можно раскрасить вершины графа G так, чтобы концы любого ребра имели разные цвета.

3.) 1).НОД :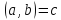 ; Найти НОД чисел: 168, 180 и 3024.

Р е ш е н и е . 168 = 2 · 2 · 2 · 3 · 7 = 23 · 31 · 71 , 180 = 2 · 2 · 3 · 3 · 5 = 22 · 32 · 51 ,

3024 = 2 · 2 · 2 · 2 · 3 · 3 · 3 · 7 = 24 · 33 · 71 .

Выпишем наименьшие степени общих делителей 2 и 3 и перемножим их: НОД = 22 · 31 = 12 .

2.НОК: , ,,

2)Алгоритм нахождения простих чисел:1)вычёркиваем кратные двум,

2.вычёркиваем кратные трём,3.после вычёркивания получаем ряд простых чисел,4.находим √n и берём ближайшее левое число к нему.

3)Функция Эйлера: Пусть дано натуральное число , представленное в виде его канонического разложения на простые сомножители

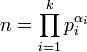
Тогда функция Эйлера может быть вычислена по формуле

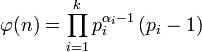
При этом полагается, что

Функцию Эйлера можно также представить в виде так называемого произведения Эйлера:

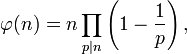
где — простое число и пробегает все значения, участвующие в разложении на простые сомножители.Также иногда функцией Эйлера называют функцию от рационального числа :

Свойства:

1. если — простое число. В частности, при имеем ;

2. если и взаимно просты. То есть Функция Эйлера мультипликативна;

3. если и взаимно просты. Так называемая теорема Эйлера;

4.

5.

если — наименьшее общее кратное, a — наибольший общий делитель.

5)Сравнения.св-ва сравнений:

Отношение сравнимости по модулю натурального числа обладает следующими свойствами:

рефлексивности: для любого целого справедливо

симметричности: если то

транзитивности: если и то,где

6) Полная система вычетов по модулю m ― любой набор из m несравнимых между собой по модулю m целых чисел. Обычно в качестве полной системы вычетов по модулю m берутся наименьшие неотрицательные вычеты

0,1,...,m − 1

или абсолютно наименьшие вычеты, состоящие из чисел

,

в случае нечётного m и чисел

в случае чётного m

7) Приведённой системой вычетов по данному модулю называется множество чисел, взятых по одному и только по одному из каждого класса вычетов по данному модулю взаимнопростого с модулем (пусть М-целое положительное число,тогда мн-во класов из пол.сист.выч. взаимно простых с m наз. Прив.сист.вычетов.)

Mпи(m)

8)Цепные дроби:Пусть сущ.конечная или бесконечная посл-ость целых чисел [a0,a1,a2,…] при чём все ai>=1,тогда выражение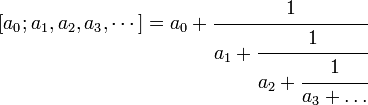 наз. Цепной дробью.

Формула Дирихле для числа делителей — асимптотическая формула

Доказательство немедленно следует из того факта, что указанная сумма равна числу целых точек с целыми положительными координатами в области, ограниченной гиперболой и осями координат.

9) конечная цепная дробь .

Алгоритм Евклида: пусть и — целые числа, не равные одновременно нулю, и последовательность чисел

определена тем, что каждое — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть

…

10)Подходящие дроби: n-ой подходящей дробью для цепной дроби , называется конечная цепная дробь , значение которой равно некоторому рациональному числу . Подходящие дроби с чётными номерами образуют возрастающую последовательность, предел которой равен . Аналогично, подходящие дроби с нечётными номерами образуют убывающую последовательность, предел которой также равен .

Эйлер вывел рекуррентные формулы для вычисления числителей и знаменателей подходящих дробей:

11) Цепной дробью последовательности (2) наз. выражение вида:

Для каждой Ц. д. (1) рекуррентные уравнения

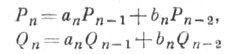
с начальными условиями

12) Цепні дроби ірраціональних чисел.

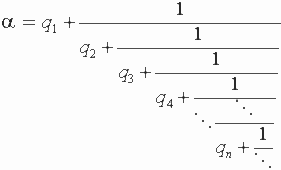
(бесконечные)

остатком цепной дроби a . Таким образом, остаток r n цепной дроби a - это весь ее "хвост" вниз и вправо, начиная с n -ого этажа. Ясно, что

13) НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ

функции x(t)функциями u(t)из фиксированного множества F- величина где - погрешность приближения (см. Прибли жения функций мера). Можно говорить о Н. п. в произвольном метрич. пространстве X, когда определяется расстоянием между элементами хи и, в этом случае Е( х, F).- расстояние от элемента хдо множества F. Если X- линейное нормированное пространство, то при фиксированном Н. п.

14)Понятие эквивалентности чисел. Понятие эквивалентности применимо к любым множествам, как конечным, так и бесконечным. Два конечных множества эквивалентны между собой тогда ( и только тогда), когда число элементов у них одинаково. Определение счетного множества можно теперь сформулировать следующим образом: множество называется счетным, если оно эквивалентно множеству натуральных чисел.

15) НЕПРЕРЫВНЫЕ ДРОБИ. Последовательность, каждый член которой является обычной дробью, порождает непрерывную (или цепную) дробь, если ее второй член прибавить к первому, а каждую дробь, начиная с третьей, прибавить к знаменателю предыдущей дроби. Например, последовательность 1, 1/2, 2/3, 3/4,..., n/(n + 1),... порождает непрерывную дробь

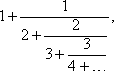
где многоточие в конце указывает на то, что процесс продолжается бесконечно. В свою очередь непрерывная дробь порождает другую последовательность дробей, называемых подходящими. В нашем примере первая, вторая, третья и четвертая подходящие дроби равны

И

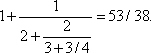
19) Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть которое не может быть представленным в виде дроби , где — целое число, — натуральное число. Представляет собой бесконечную непериодическую десятичную дробь. О существовании иррациональных чисел, точнее отрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа

НЕСОКРАТИМАЯ ДРОБЬ — дробь, числитель и знаменатель которой не имеют общих делителей; напр., 3/5, 16/9