
- •1. Содержание дисциплины
- •2. Тематика практических работ Работы выполняются на компьютерах по типовым программам с заданием индивидуальных параметров моделирования, расчетов и обработки данных для каждого студента группы.
- •Содержание
- •1.1. Общие сведения и понятия [1,10, 15, 25]
- •Содержание
- •1.2. Типы сигналов [1,10,15]
- •1.3. Системы преобразования сигналов [1, 9, 14, 18]
- •1.4. Информационная емкость сигналов [10,12,28]
- •Литература
- •Содержание
- •Введение
- •2.1. Пространство сигналов [1,3,16,29].
- •2.2. Мощность и энергия сигналов [1, 3, 16].
- •2.3. Пространства функций [1,3,11,16,29].
- •2.4. Функции корреляции сигналов [1, 25, 29].
- •2.5. Математическое описание шумов и помех [1, 30].
- •Литература
- •Содержание
- •Введение
- •3.1. Разложение сигналов по единичным импульсам [1, 11].
- •3.2. Свертка (конволюция) сигналов [1, 11].
- •Литература
- •Содержание
- •Введение
- •5.1. Мощность и энергия сигналов [1,3,16].
- •5.2. Энергетические спектры сигналов [1].
- •Литература
- •Содержание
- •Введение
- •6.1. Автокорреляционные функции сигналов [1,25].
- •6.2. Взаимные корреляционные функции сигналов [1,19].
- •6.3. Спектральные плотности корреляционных функций [1,25].
- •Литература
- •Лекция 8. Дискретизация сигналов Содержание
- •Введение.
- •7.1. Задачи дискретизации функций [10, 21].
- •7.2. Равномерная дискретизация [16,21].
- •7.3. Дискретизация по критерию наибольшего отклонения [10].
- •7.4. Адаптивная дискретизация [10].
- •7.5. Квантование сигналов [5,21].
- •7.6. Децимация и интерполяция данных [4,5,17].
- •Литература
- •Содержание
- •Введение
- •8.1. Преобразование Фурье [5,17,21].
- •8.2. Преобразование Лапласа.
- •8.4. Дискретная свертка (конволюция) [5,17,21].
- •Литература
- •Содержание
- •Введение.
- •9.1. Случайные процессы и функции [1, 2, 25].
- •9.2. Функции спектральной плотности [2,25,26].
- •9.3. Преобразования случайных функций [1, 26, 27].
- •9.4. Модели случайных сигналов и помех [2, 28].
- •Литература
2.4. Функции корреляции сигналов [1, 25, 29].
Функции корреляции сигналов применяются для интегральных количественных оценок формы сигналов и степени их сходства друг с другом.
Автокорреляционные функции (АКФ) сигналов (correlation function, CF). Применительно к детерминированным сигналам с конечной энергией АКФ является количественной интегральной характеристикой формы сигнала, и представляет собой интеграл от произведения двух копий сигнала s(t), сдвинутых относительно друг друга на время :
Bs()
=  s(t)
s(t+)
dt. (2.4.1)
s(t)
s(t+)
dt. (2.4.1)
Как следует из этого выражения, АКФ является скалярным произведением сигнала и его копии в функциональной зависимости от переменной величины значения сдвига . Соответственно, АКФ имеет физическую размерность энергии, а при = 0 значение АКФ непосредственно равно энергии сигнала:
Bs(0)
=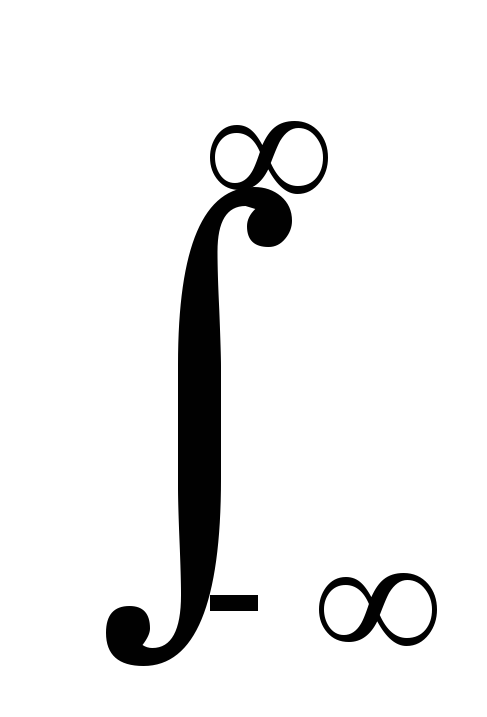 s(t)2
dt = Es.
s(t)2
dt = Es.
Функция АКФ является непрерывной и четной. В последнем нетрудно убедиться заменой переменной t = t- в выражении (2.4.1):
Bs()
= s(t-)
s(t) dt =
s(t-)
s(t) dt =  s(t)
s(t-
) dt = Bs(-).
(2.4.1')
s(t)
s(t-
) dt = Bs(-).
(2.4.1')
С учетом четности, графическое представление АКФ обычно производится только для положительных значений . На практике сигналы обычно задаются на интервале положительных значений аргументов от 0-Т. Знак + в выражении (2.4.1) означает, что при увеличении значений копия сигнала s(t+) сдвигается влево по оси t и уходит за 0, что требует соответствующего продления сигнала в область отрицательных значений аргумента. А так как при вычислениях интервал задания обычно много меньше интервала задания сигнала, то более практичным является сдвиг копии сигнала влево по оси аргументов, т.е. применение в выражении (2.4.1) функции s(t-) вместо s(t+ ).
По мере увеличения значения величины сдвига для финитных сигналов временное перекрытие сигнала с его копией уменьшается и скалярное произведение в целом стремятся к нулю.
Пример. На интервале (0,Т) задан прямоугольный импульс с амплитудным значением, равным А. Вычислить автокорреляционную функцию импульса.
П ри
сдвиге копии импульса по оси t вправо,
при 0≤≤T
сигналы перекрываются на интервале от
до Т. Скалярное произведение:
ри
сдвиге копии импульса по оси t вправо,
при 0≤≤T
сигналы перекрываются на интервале от
до Т. Скалярное произведение:
Bs()
= A2
dt = A2(T-).
A2
dt = A2(T-).
П ри
сдвиге копии импульса влево, при -T≤<0
сигналы перекрываются на интервале от
0 до Т-.
Скалярное произведение:
ри
сдвиге копии импульса влево, при -T≤<0
сигналы перекрываются на интервале от
0 до Т-.
Скалярное произведение:
Bs()
=
 A2
dt = A2(T+).
A2
dt = A2(T+).
При || > T сигнал и его копия не имеют точек пересечения и скалярное произведение сигналов равно нулю (сигнал и его сдвинутая копия становятся ортогональными).
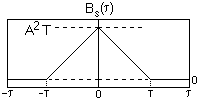 Обобщая
вычисления, можем записать:
Обобщая
вычисления, можем записать:
Bs()
=![]() .
.
В случае периодических сигналов АКФ вычисляется по одному периоду Т, с усреднением скалярного произведения и его сдвинутой копии в пределах периода:
Bs()
= (1/Т)![]() s(t)
s(t-)
dt.
s(t)
s(t-)
dt.
Рис. 2.4.1.

Отметим, что полученный результат не зависит от начальной фазы гармонического сигнала, что характерно для любых периодических сигналов и является одним из свойств АКФ.
Для сигналов, заданных на определенном интервале [a, b], вычисление АКФ производится с нормировкой на длину интервала [a, b]:
Bs()
= s(t)
s(t+)
dt. (2.4.2)
s(t)
s(t+)
dt. (2.4.2)
Автокорреляция сигнала может оцениваться и коэффициентом автокорреляции, вычисление которого производится по формуле (по центрированным сигналам):
rs() = cos () = s(t), s(t+) /||s(t)||2.
Взаимная корреляционная функция (ВКФ) сигналов (cross-correlation function, CCF) показывает как степень сходства формы двух сигналов, так и их взаимное расположение друг относительно друга по координате (независимой переменной), для чего используется та же формула (2.4.1), что и для АКФ, но под интегралом стоит произведение двух разных сигналов, один из которых сдвинут на время :
B12()
=  s1(t)
s2(t+)
dt. (2.4.3)
s1(t)
s2(t+)
dt. (2.4.3)
При замене переменной t = t- в формуле (2.4.3), получаем:
B12()
= s1(t-)
s2(t)
dt =
s1(t-)
s2(t)
dt = s2(t)
s1(t-)
dt = B21(-)
s2(t)
s1(t-)
dt = B21(-)
Рис. 2.4.2. Сигналы и ВКФ.

При =0 сигналы ортогональны и значение B12()=0. Максимум В12() будет наблюдаться при сдвиге сигнала s2(t) влево на значение =1, при котором происходит полное совмещение сигналов s1(t) и s2(t+). При вычислении значений B21(-) аналогичный процесс выполняется последовательным сдвигом сигнала s1(t) вправо по временной оси с постепенным увеличением отрицательных значений , а соответственно значения B21(-) являются зеркальным (относительно оси t=0) отображением значений B12(), и наоборот. На рис. 2.4.3 это можно видеть наглядно.
Рис. 2.4.3. Сигналы и ВКФ.

Для периодических сигналов понятие ВКФ обычно не применяется, за исключением сигналов с одинаковым периодом, например, сигналов входа и выхода систем при изучении характеристик систем.
Коэффициент взаимной корреляции двух сигналов вычисляется по формуле (по центрированным сигналам):
rsv() = cos () = s(t), v(t+) /||s(t)|| ||v(t)||. (2.4.4)
Значение коэффициента взаимной корреляции может изменяться от -1 до 1.
