5 Дослідження виробничої регресії коБба-дугласа

5.1 Мета роботи

Користуючись пакетом EXCEL знайти оцінки виробничої регресії за методом найменших квадратів.

5.2 Методичні вказівки щодо організації самостійної роботи студентів

Під час підготовки до виконання даної лабораторної роботи слід вивчити теоретичний матеріал за лекційним матеріалом та Додатки А,Г.

У сфері виробництва при аналізі кількісного співвідношення показника і факторів у ролі показника можуть виступати: обсяг випущеної продукції, прибуток, товарообіг, рентабельність, собівартість одиниці продукції, фондо- віддача й інше. Факторами для цих показників можуть бути: робоча сила, основні засоби або капітал, земля та й надра, продуктивність суспільної праці, рівень розвитку науки, техніки, освіти та ін.

У більш вузькому значенні під виробничою регресією розуміють залежність між обсягом виробництва (індексом виробництва) і величиною різних виробничих ресурсів. У загальному вигляді виробнича регресія може бути записана так:

, (5.1)

де Y – обсяг виробленої продукції;

Х₁, Х₂, ... , Х_m – фактори, що визначають обсяг виробництва.

Виробнича регресія може використовуватися як на мікрорівнях, так і на макрорівнях. У випадку макроекономічної виробничої регресії народне господарство розглядається як єдина система, що функціонує за принципом “витрати-випуск”.

При побудові і використанні моделі виробничої регресії слід пам'ятати, що результати обсягу виробництва згладжуються (усереднюються), разом з тим побудована модель дає можливість зробити якісний аналіз виробництва в цілому. Двофакторна виробнича регресія показує, як обсяг виробленої продукції Y взагалі залежить від двох цінових факторів: чисельності робочої сили X₁ та основних засобів (капіталу) даної галузі Х₂.

. (5.2)

Нехай у результаті досліджень отримано такі статистичні дані

у_i, x_1i, x_2i ,

де у_i – обсяг випуску продукції в i-му періоді (підприємстві),

x_1i – чисельність робочої сили в цьому періоді,

x_2i – основний капітал за цей період.

На основі статистичних даних необхідно оцінити параметри виробничої регресії. Для оцінки параметрів лінії регресії прологарифмуємо рівняння і виконаємо заміну величин

; (5.3)

. (5.4)

Після цих перетворень отримаємо лінійну модель

. (5.5)

Якщо використовуємо метод найменших квадратів для отримання оцінок параметрів а₀₁, а₁, а₂ (див. лабораторну роботу 2).

Система нормальних рівнянь для оцінок параметрів цієї регресії в матричній формі має вигляд

де

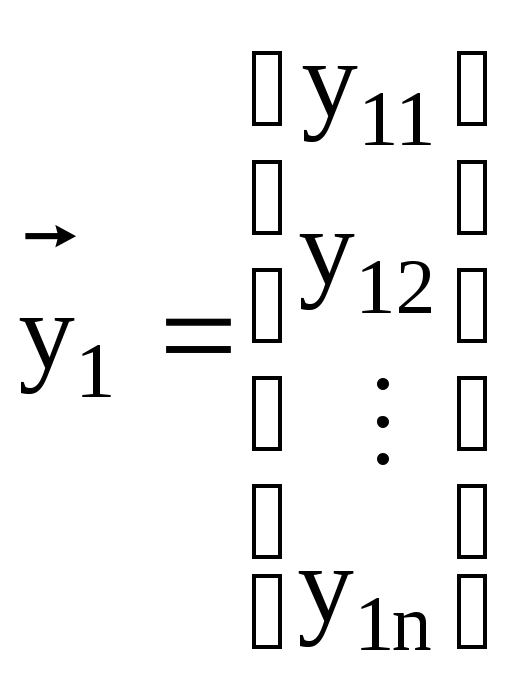; . (5.6)

Після розв'язування системи рівнянь отримаємо оцінку вектора параметрів:

. (5.7)

Якщо фактори виробничої регресії X_i назвати ресурсами, то для кожного ресурсу маємо визначити граничну продуктивність випуску продукції по даному ресурсу, частинний коефіцієнт еластичності та ін.

Для багатофакторної регресії частинний коефіцієнт еластичності показує, на скільки відсотків зміниться показник, якщо один із факторів зміниться на один відсоток при незмінних значеннях інших факторів.

Якщо лінія регресії має вигляд Y=f(Х₁, Х₂,...Х_i,...Х_m), то частинний коефіцієнт еластичності для фактора X_i обчислюється за формулою

(5.8)

Знайдемо частинні коефіцієнти еластичності для вироб­ничої регресії Кобба-Дугласа:

. (5.9)

Таким чином, параметр a₁ є частинним коефіцієнтом еластичності фактора X₁ виробничої регресії Кобба-Дугласа і показує, що показник Y змінюється на а₁ відсотків, якщо фактор X₁ змінюється на 1% при незмінних значеннях фактора Х₂. Оскільки коефіцієнт еластичності додатний, то збільшення (зменшення) фактора викликає, відповідно, збільшення (зменшення) показника.

Аналогічним чином знайдемо, що частинний коефіцієнт еластичності для другого фактора дорівнює другому параметру k_X2=а₂ і, відповідно, показує, що зміна фактора Х₂ на 1 % викликає зміну показника на а₂ відсотків при незмінних значеннях фактора Х₁.

Геометрично виробничу регресію можна зобразити як поверхню в тривимірному просторі з координатами Х₁, Х₂, Y.

Для більш повного уявлення виробничої регресії розглянемо її ізокванти. В тих виробництвах, де фактори взаємозамінні, одного й того ж результату (обсягу випуску продукції) можна досягти різною комбінацією факторів виробництва (основних засобів і праці).

Для регресії, що розглядається, геометричне місце точок факторів Х₁, Х₂ (різні комбінації факторів), для яких показник обсягу виробництва продукції Y залишається сталим, називається ізоквантою.

Нехай кінцева мета виробництва – виробити продукцію обсягом Y_o. Припустимо, що для даного виробництва оцінені параметри виробничої регресії. Необхідно знайти комбінацію факторів, при яких буде вироблено продукції Y_o, тобто необхідно знайти рівняння ізокванти.

Щоб побудувати ізокванту, необхідно виразити один з факторів виробничої регресії через інший фактор і стале значення показника регресії:

(5.10)

Якщо сталу b позначити через, то отримаємо таку залежність

(5.11)

в окремому випадку при а₂=а₁ отримаємо гіперболу

(5.12)

Сімейство ізоквант у декартовій системі координат X₁0X₂ зображено на рис.5.1.

Згідно з рис.5.1 при різних значеннях факторів у точках

буде вироблено однаковий обсяг даного виду продукції, тобто

.

Таким же чином можна розглянути ряд комбінацій факторів, яким відповідає інший сталий обсяг виробництва продукції. Це буде інша ізокванта із сімейства ізоквант. Наприклад, на рис.5.1 зображена ізокванта, якій відповідає сталий обсяг Y₁ виробництва продукції.

Рисунок 5.1 – Сімейство ізоквант

5.3 Порядок виконання роботи

1. Скласти систему нормальних рівнянь для оцінки параметрів виробничої регресії (Додаток В).

2. Сформувати матриці показника та факторів виробничої регресії.

3. Вирішити матричне рівняння (5.7) та знайти оцінки параметрів виробничої регресії, користуючись вбудованими у EXCEL функціями МОПРЕД, ТРАНСП, МОБР, МУМНОЖ (Додаток Г).

4. З надійністю Р=0.95 встановити адекватність прийнятої математичної моделі статистичним даним. Використати статистичні функції FРАСП, ДИСП, СРЗНАЧ.

5. Якщо модель адекватна статистичним даним, тоді знайти частинні коефіцієнти еластичності, значення прогнозу, його надійний інтервал.

6. Використовуючи графічні можливості пакета EXCEL, побудувати ізокванти.

6. Використовуючи розрахунки, зробити висновки.

5.4 Зміст звіту

1. Вихідні дані.

2. Проміжні результати вирішення матричного рівняння (5.7): вихідна, транспонована, обернена матриці та результати множення матриць.

3. Вектор оцінок параметрів виробничої регресії.

4. Результати перевірки адекватності моделі статистичним даним.

5. Частинні коефіцієнти еластичності.

6. Висновки.

5.5 Контрольні запитання та завдання

1. Наведіть визначення та зміст виробничої регресії.

2. Як привести нелінійну регресію до лінійної?

3. Як скласти систему нормальних рівнянь для оцінки параметрів приведеної лінійної регресії?

4. Викладіть методику розв’язання системи лінійних рівнянь за допомогою можливостей пакета EXCEL.

5. Як оцінити адекватність прийнятої моделі статистичним даним?

6. Як знайти оцінки частинних коефіцієнтів еластичності?