1. Случайные события, их виды.

Случайные события:

Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти. Например, бросание монеты.

Виды:

События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие.

События называют равновозможными, если есть оснооснования считать, что ни одно из них не является более возможным, чем другое.

2. Классическое определение вероятности, ее свойства.

Каждый из возможных результатов испытания (испытание состоит в извлечении шара из

урны) назовем элементарным исходом (элементарным событием). Те элементарные исходы, в которых интересующее нас событие наступает, назовем благоприятствующими этому событию.

Определение:

Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных

исходов, образующих полную группу. Итак, вероятность события А определяется формулой

Свойства:

1. Вероятность достоверного события равна единице.

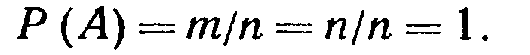
2. Вероятность невозможного события равна нулю.

3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

3. Относительная частота, ее свойства.

Определение:

Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний., n – общее количество фактически проыедённых испытаний, еол-во испытнаий в которых наблюдалось событие А. Вероятность вычисляют до опыта, а относительную частоту — после опыта.

Свойства:

1. h(A)=0 невозможное событие

2. h(A)=1 достоверное событие

3. 0<h(A)<1 случайное событие

4. Общиц случай:

4. Суммирование вероятностей несовместимых событий.

Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий.

Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.

Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

5. Полная группа событий, противоположные события.

Полная группа событий:

Теорема. Сумма вероятностей событий ,..., образующих полную группу, равна единице.

Доказательство. Так как появление одного из событий полной группы достоверно, а вероятность достоверного события равна единице, то (*). Любые два события полной группы несовместны, поэтому можно применить теорему сложения: (**) Сравнивая (*) т (**) получим.

Противоположные события:

Противоположными называют два единственно возможных события, образующих полную группу.

Если одно из двух противоположных событий обозначено через А, то другое принято обозначать .

Теорема: Сумма вероятностей противоположных событий равна единице:

Доказательство. Противоположные события образуют полную группу, а сумма вероятностей событий, образующих полную группу, равна единице.