24. Определение ускорения точки в сложном движении. Ускорение Кориолиса.

 Определение скоростей и ускорений точек в сложном движении

Теоремы о скоростях и ускорениях точек в сложном движении изложены во всех учебниках по теоретической механике.

Абсолютная скорость точки определяется как геометрическая сумма переносной и относительной скоростей:

Каждое слагаемое в этой формуле определяется независимо друг от друга, исходя из соответствующего закона движения. В примере на рисунке 3.2 относительная скорость V_r  определяется с учетом закона движения точки по оси Oy .

Переносная скорость определится как скорость точки M  при вращении вместе с квадратом вокруг оси его вращения. Величина абсолютной скорости может быть определена с помощью теоремы косинусов:

Для определения вектора абсолютной скорости можно равенство (3.1) спроецировать на выбранные оси координат, найти проекции абсолютной скорости, её величину и направляющие косинусы, то есть определить углы, которые вектор скорости составляет с выбранными осями.

Ускорение точки определяется как сума трех ускорений: переносного, относительного и кориолисова (поворотного):

Первые два слагаемые этой формулы определяются из соответствующих законов переносного и относительного движений. В случае неравномерных криволинейных движений эта формула имеет вид

Кориолисово ускорение определяется по формуле:

Величина этого ускорения a_K=2ω_eV_rsinα , (3.5)

где  α - угол между векторами переносной угловой и линейной относительной скоростями.

Направление кориолисова ускорения определяется двумя правилами:

1) Правило векторного произведения

Согласно этому правилу вектор кориолисова ускорения перпендикулярен векторам ω_e  и V_r  (или плоскости, проходящей через эти вектора,  проведенные из одной точки). Направлен вектор a_K  так, что если смотреть ему навстречу, то кратчайший поворот вектора ω_e  до совмещения с вектором V_r  происходит против хода часовой стрелки (рисунок 3.3).

Рисунок 3.3

2) Правило Жуковского

Для определения направления кориолисова ускорения нужно спроецировать вектор относительной скорости в плоскость, перпендикулярную вектору переносной угловой скорости и полученную проекцию повернуть на   в сторону переносного вращения (рисунок 3.4).

Рисунок 3.4

Из формулы (3.5) видно, что кориолисово ускорение равно нулю, если

- равна нулю относительная скорость;

- переносное движение - поступательное (ω_e=0 );

- угол между  ω_e  и V_r  равен 0^o  или 180_o  (вектор V_r  параллелен оси переносного вращения).

Абсолютное ускорение точки определяется по аналогии с определением её скорости. Формула (3.3) проецируется на выбранные оси координат, и находятся проекции абсолютного ускорения на эти оси:a_x, a_y, a_z. Величина ускорения определяется по формуле:

Направление вектора абсолютного ускорения определяется с помощью направляющих косинусов, то есть определяются углы, которые вектор ускорения составляет с осями координат:

Согласно теореме Кориолиса, абсолютное ускорение точки в сложном движении определяется как геометрическая сумма относительного, переносного и кориолисова ускорений (рис. 3)

a_a = a_r  ⊕   a_e  ⊕  a_C   .

Рис. 3

Поскольку, в данном случае, относительное движение происходит по прямой линии, относительное ускорение a_r  направлено вдоль этой прямой и определяется выражением

Переносным ускорением точки M является ускорение точки M диска. Диск совершает вращательное движение, следовательно, переносное ускорение определяется выражением

a_e = a_e^вр  ⊕  a_e^цс            ,

где  a_e^вр= ε⋅ OM  - вращательное ускорение точки M, направленное перпендикулярно отрезку OM ;

a_e^цс= ω²⋅ OM - центростремительное ускорение точки M, направленное к центру диска.

Ускорение Кориолиса или поворотное ускорение определяется по формуле

a_C = 2 ω_e  ⊗  ν_r          ,

где  ω_e - переносная угловая скорость,

ν_r  - относительная скорость точки.

Направление ускорения Кориолиса определяется по правилу векторного произведения или по правилу Жуковского.

Величина ускорения Кориолиса определяется выражением

a_C = 2 ω_e  ν_r  sinα      ,

где  α  – угол между векторами ω_e  и ν_r  .

Рассмотрим, какой физический смысл заложен в ускорение Кориолиса. Для простоты будем считать, что диск вращается с постоянной угловой скоростью, а точка M движется относительно диска с постоянной относительной скоростью (рис.4).

Рис. 4

Пусть в момент времени t₁ точка M занимала положение M₁ и имела относительную скорость ν_{r 1} . За промежуток времени Δt точка M переместится в положение M₂ , при этом направление скорости ν_r изменится вследствие вращения диска. Вектор ν_r получит приращение Δν_r . Отношение  Δν_r / Δt определяет среднее ускорение точки за промежуток времени Δt . Предел отношения  Δν_r / Δt при  Δt→ 0 есть производная  dν_r /dt , как производная от вектора постоянного по величине.

Рассмотрим, как изменяется переносная скорость в зависимости от относительного движения. В моменты времени t₁ и t₂ переносная скорость определяется выражениями ν_e1= ω ⊗ OM₁  и  ν_e2= ω ⊗ OM₂ . Тогда приращение вектора  ν_e за счет относительного движения будет равно

Δν_e = ω  ⊗ OM₂ - ω ⊗  OM₁ = ω  ⊗ (OM₂ - OM₁) = ω ⊗  ν_r⋅ Δt

Отношение Δν_e / Δt в пределе при  Δt→ 0 дает производную dν_e / d t = ω ⊗  ν_r  . Таким образом, ускорение Кориолиса с одной стороны характеризует изменение относительной скорости по направлению за счет переносного вращения и, с другой стороны, изменение величины переносной скорости за счет относительного движения.

Рис. 5

Абсолютное ускорение точки в сложном движении в общем случае определяется геометрической суммой пяти слагаемых

Для определения величины абсолютного ускорения удобнее пользоваться аналитическим методом сложения векторов:

25. Предмет динамики. Основные понятия и определения: масса, материальная точка, сила; постоянные и переменные силы. Законы классической механики. Инерциальная система отсчета. Задачи динамики.

В динамике объектом изучения являются материальная точка , твердое тело , механические системы.

Сила-мера механического взаимодействия тел , определяющаяся интенсивностью и направлением.

Масса — физическая величина, отвечающая за способность физических тел сохранять своё поступательное движение (инертности), а также характеризующая количество вещества.  Под массой понимают два различных свойства вещества:  1.инертная масса, которая характеризует меру инертности тел и фигурирует во втором законе Ньютона;  2.гравитационная масса, которая определяет, с какой силой тело взаимодействует с внешними гравитационными полями (пассивная гравитационная масса) и какое гравитационное поле создаёт само это тело (активная гравитационная масса). 

Материальная точка - это тело, размерами которого в данной ситуации можно пренебречь.

 Первый закон: всякое тело пребывает в состоянии покоя или равномерного прямолинейного движения до тех пор, пока действующие на него силы не изменят это состояние.

Второй закон классической механики гласит: произведение массы тела на его ускорение равно действующей силе, а направление ускорения совпадает с направлением силы. Такова его современная формулировка. Ньютон сформулировал его иначе: изменение количества движения пропорционально приложенной действующей силе и происходит по направлению той прямой, по которой эта сила действует. Т.е. Ньютон в формулировке второго закона оперирует понятием количества движения, понимаемым как мера движения, пропорциональная массе и скорости. Количество движения - величина векторная (Ньютон учитывал направление движения при формулировании правила параллелограмма скоростей).Но это понятие в истории науки не удержалось (и сейчас заменено понятием импульса), поскольку было неясно, чем измерять движение. Декарт количество движения измерял произведением массы на скорость, Лейбниц - произведение массы на квадрат скорости (называя количество движения живой силой). Между сторонниками первого и второго возникла дискуссия. Даламбер показал эквивалентность обеих мер измерения (если, например, тело тормозится под действием силы, то тормозящая сила определяется количеством движения mv, если известно время торможения, и выводится из mv2/2, если известен путь торможения). Истинная суть обеих мер движения будет выяснена позже, когда будет открыт закон сохранения энергии.

Третий закон классической механики гласит: действию всегда есть равное и противоположное противодействие, иначе взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны. Иначе говоря, силы, с которыми действуют два тела друг на друга, равны по величине и направлены в противоположные стороны. Ньютон распространил действие третьего закона на случай и столкновения тел, и на случай их взаимного притяжения.

Из трех фундаментальных законов движения Ньютона вытекают следствия, одно из которых - сложение количества движения по правилу параллелограмма. Если Декарт исходил из признания неизменности количества движения в мире, то Ньютон придерживался противоположного мнения.

Ускорение тела зависит от величин, характеризующих действие других тел на данное тело, а также от величин, определяющих особенности этого тела.

Инерциальные системы отсчета – это системы, относительно которых материальная точка при отсутствии на нее внешних воздействий или их взаимной компенсации покоится или движется равномерно и прямолинейно. 

Задачи динамики

Исторически деление на прямую и обратную задачу динамики сложилось следующим образом.

• Прямая задача динамики: по заданному характеру движения определить равнодействующую сил, действующих на тело.

• Обратная задача динамики: по заданным силам определить характер движения тела.

26.Дифференциальные уравнения движения материальной точки в декартовых прямоугольных координатах и в проекциях на оси естественного трехгранника. Две основные задачи динамики для материальной точки.

Дифференциальные уравнения движения материальной точки в декартовых координатах:

m*d^2x/dt^2=ΣFkx, m*d^2y/dt^2=ΣFky, m*d^2z/dt^2=ΣFkz

Дифференциальные уравнения движения материальной точки в проекциях на оси естественного трёхгранника:

Проекция на 3. на Mτnb: m*dv/dt=ΣFkτ, m*dv/dt=ΣFkn, m*dv/dt=ΣFkb

Суть первой задачи динамики материальной точки состоит в том, чтобы при известных массе точки и законе её движения, найти величину и направление силы, действующей на точку. Решение этой задачи связано с дифференцированием уравнений движения материальной точки.

 Материальная точка массой кг совершает движение согласно уравнениям (x,y-в м,t-с). Определить величину силы F, под действием которой движется точка.

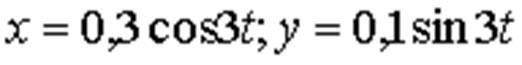Решение Из дифференциальных уравнений движения материальной точки имеем

 

 

, но Поэтому:где r-модуль радиуса- вектора движущейся точки.

Вторая задача динамики материальной точки заключается в том, чтобы по известной массе точки и силе действующей на неё установить закон движения точки. Её решение сводится к интегрированию дифференциальных уравнений движения и к определению постоянных интегрирования по начальным условиям.

27.Решение первой задачи динамики. Решение второй задачи динамики. Постоянные интегрирования и их определение по начальным условиям.