5.2. Производные высших порядков от функций, заданных параметрически

Пусть функция y, зависящая от x, задана параметрически на интервале Т:

,

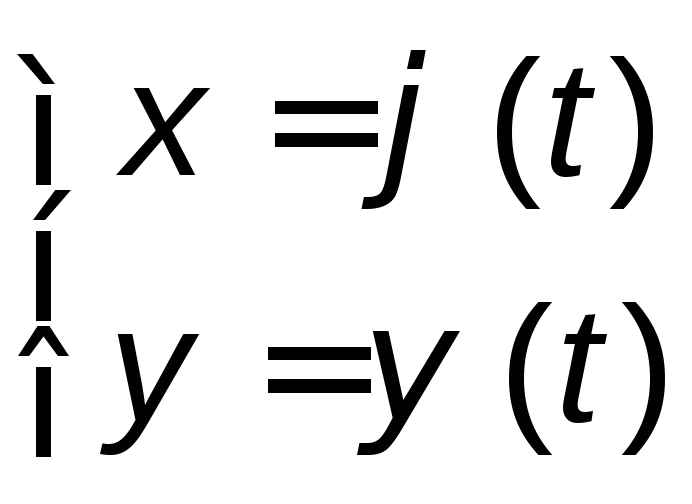Найдем . Известно, что==(п. 4.3), поэтому

= ===.

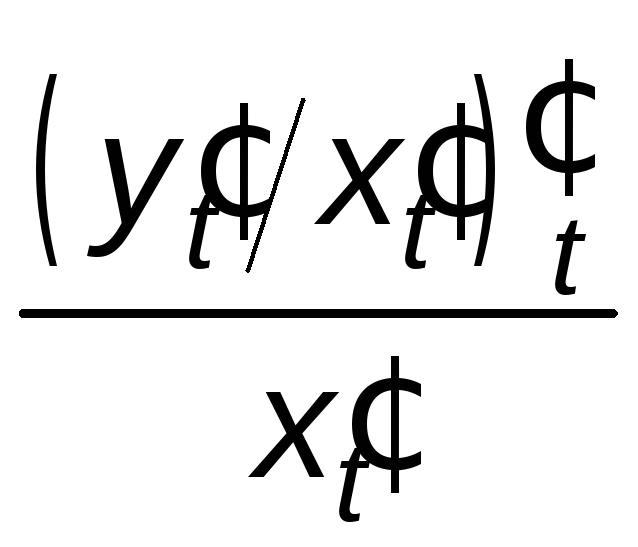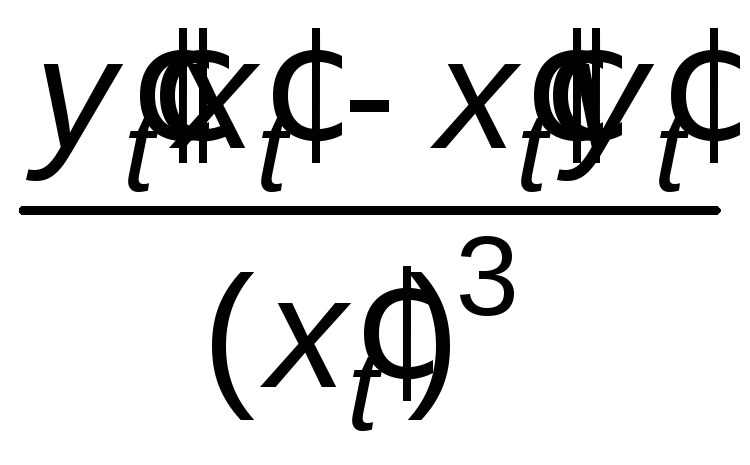Аналогично будет вычисляться и т. д.

Пример 5.3. Найти идля функции, заданной параметрически:

.

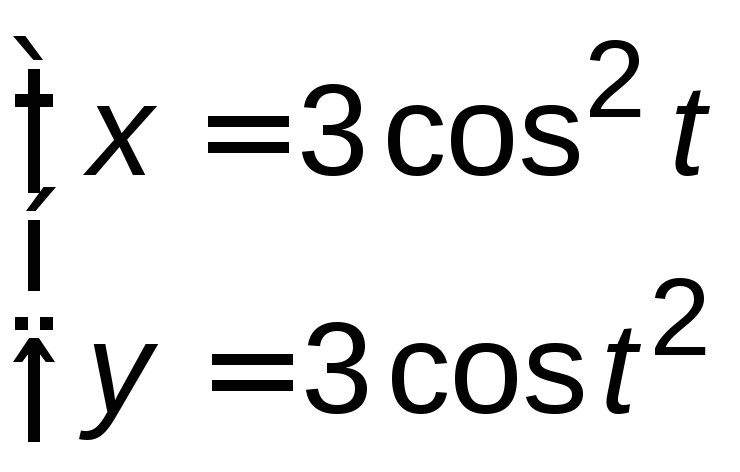Решение.

;

;

;

;

;

=

.

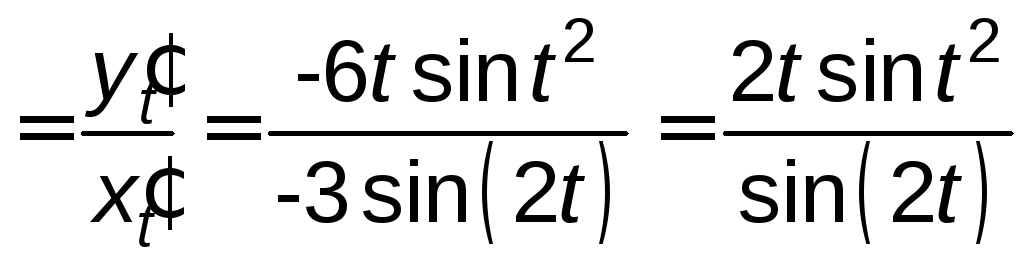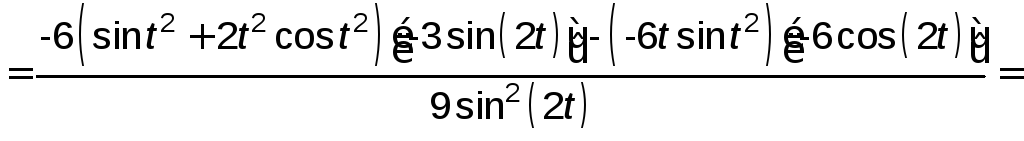
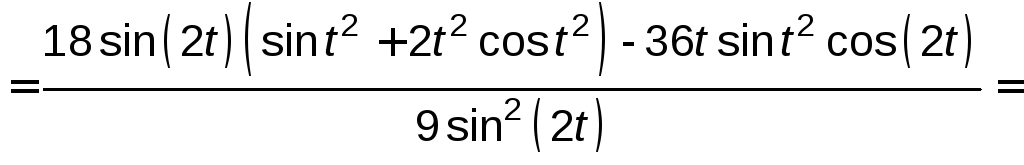
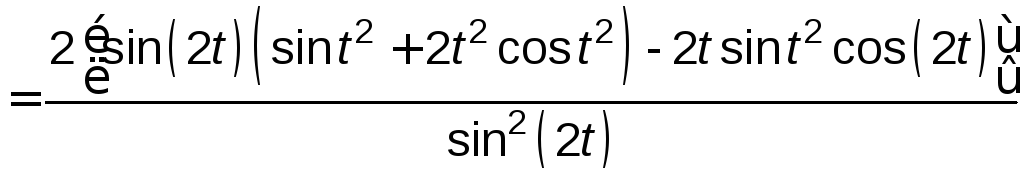Пример 5.4. Функция y от x задана параметрически уравнениями:

, .

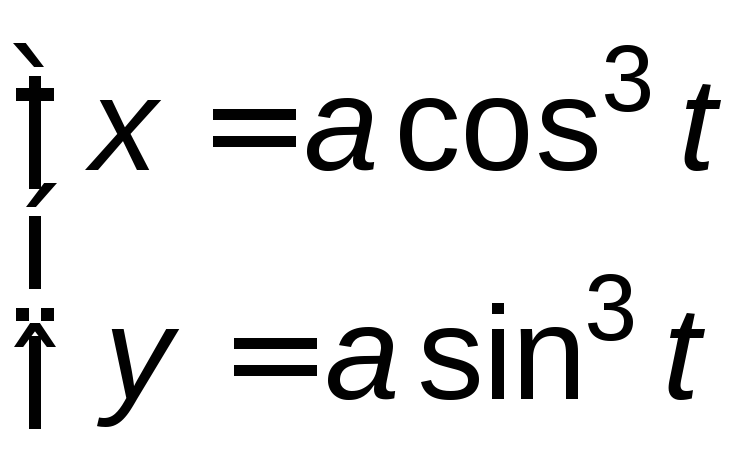Найти .

Решение.

====;

===-=.

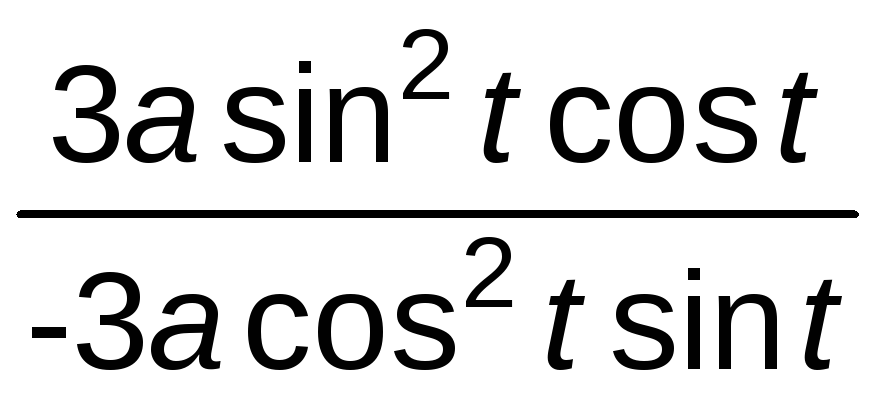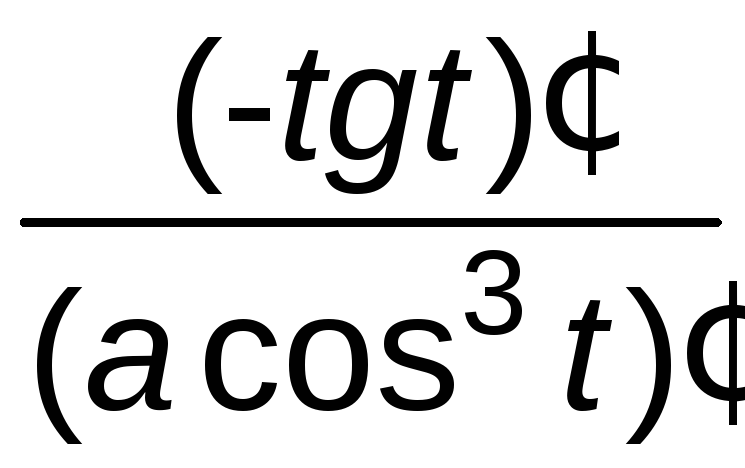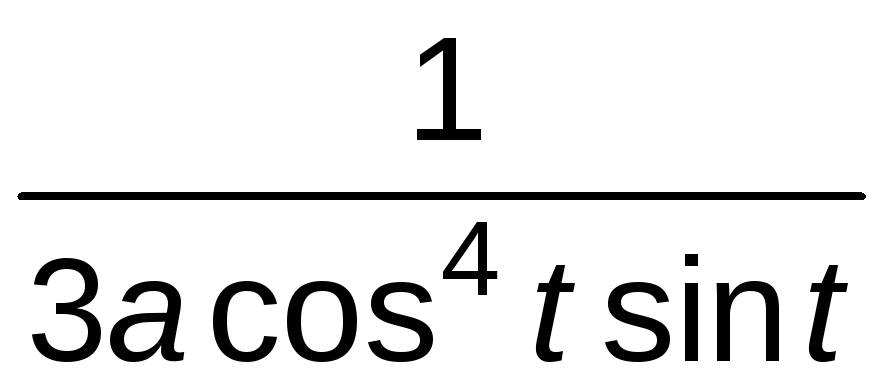5.3. Производные высших порядков от функций, заданных неявно

Нахождение производных высших порядков от функций, заданных неявно, рассмотрим на примере.

Пример 5.5. Найти ,для функции, заданной неявно уравнением:. Вычислитьy'(0), y''(0).

Решение.

Найдем сначала y', как описано в п.4.2.

,

,

,

=.

Для нахождения y'' будем дифференцировать равенство , получим:

.

Отсюда найдем y'' и подставим найденное выражение для y': ,

y''=–===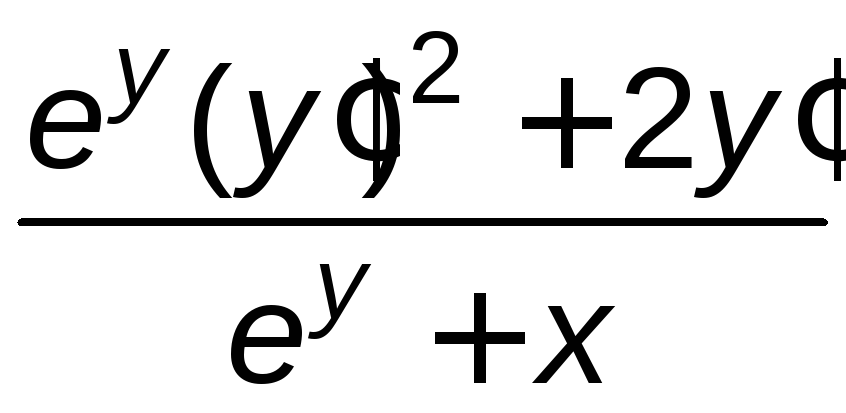

= .

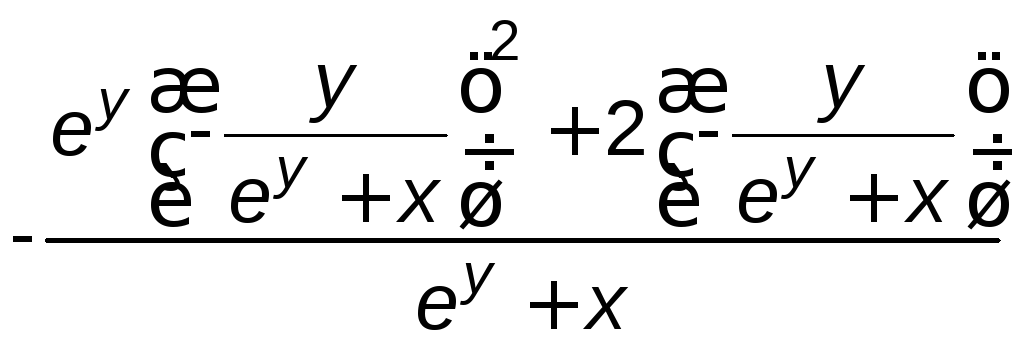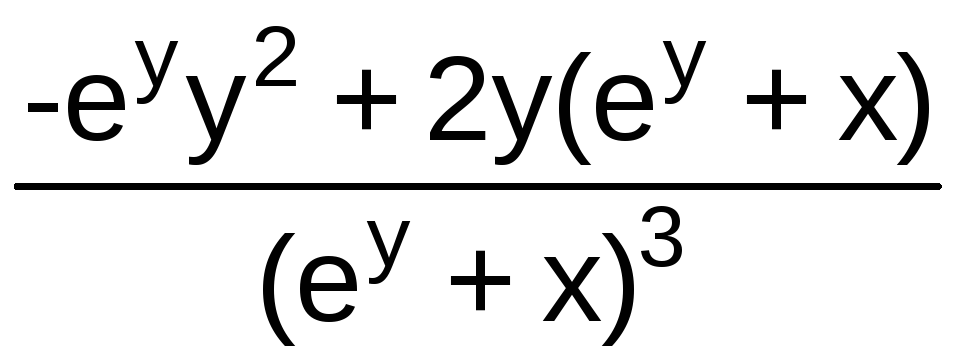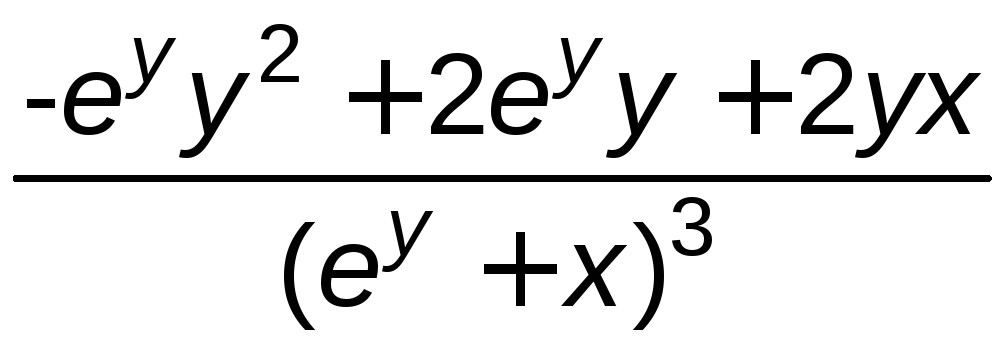Итак, y'=–,

y''=.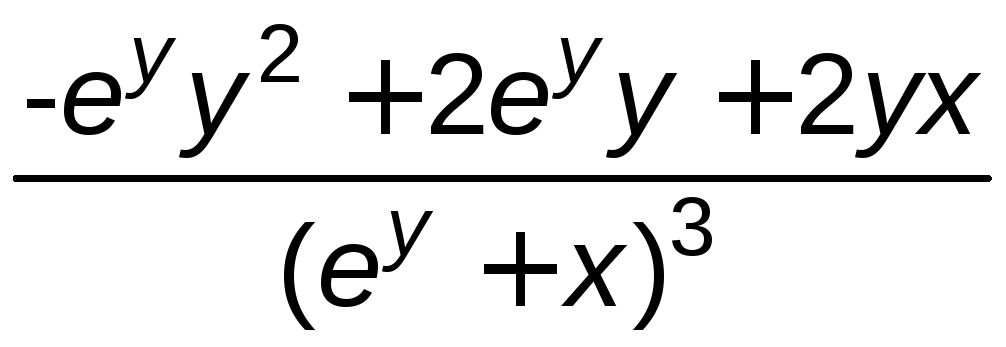

Подставим x=0 в исходное уравнение , получим:

, откуда y=1, значит,

y(0)=1; y'(0)=–;y''(0)==.

6. Правило Лопиталя

Рассмотрим новый способ нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, т.е. раскрытия неопределенностей типа и, так называемоеправило Лопиталя.

Теорема Лопиталя 1 (раскрытие неопределенностей типа ). Пусть функции,определены, непрерывны и дифференцируемы в точкеx₀и некоторой ее окрестности, причемдля любогоxиз этой окрестности, и пусть,(следовательно,,– бесконечно малые при). Еслисуществует, то существуети

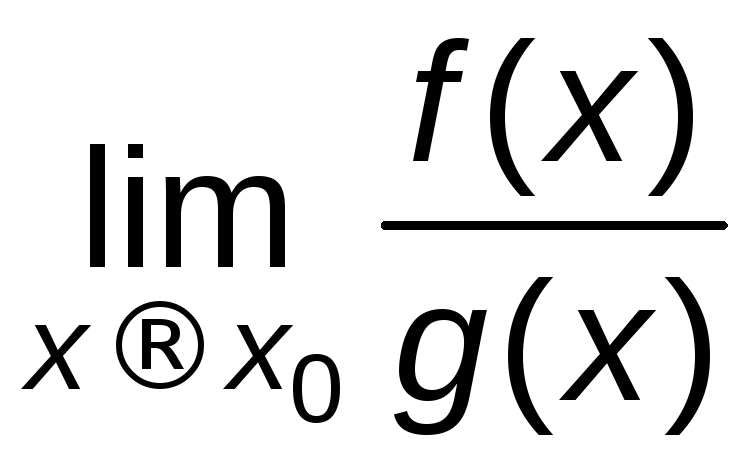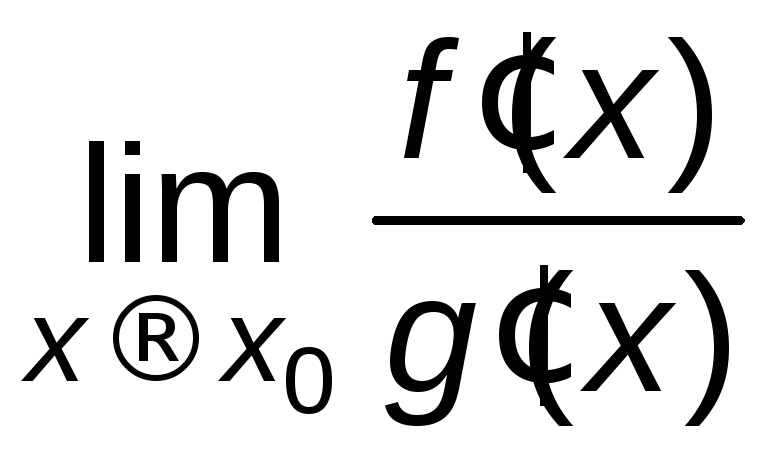=. (6.1)

Пример 6.1. Найти .

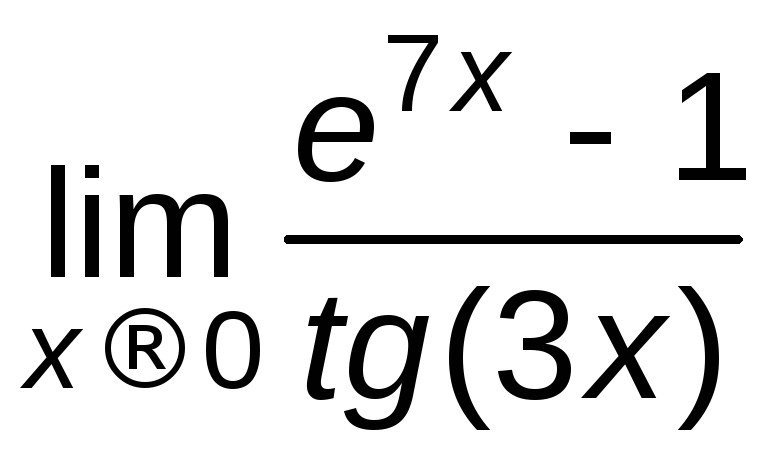Решение.

Так как при функции и ,то имеем неопределенность типа . Числитель и знаменатель данной дроби непрерывны дифференцируемы и стремятся к нулю. Это означает, что можно применить правило Лопиталя:

.

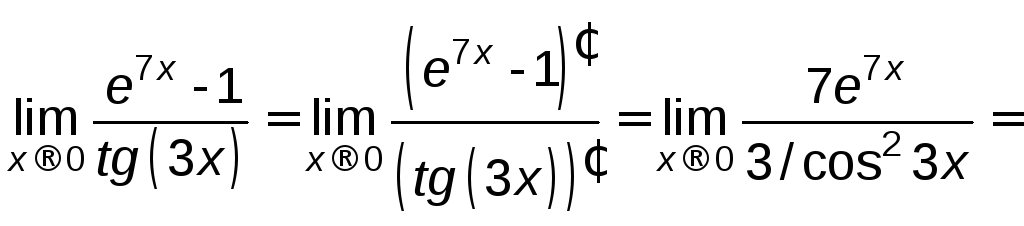
Пример 6.2. Найти .

Решение.

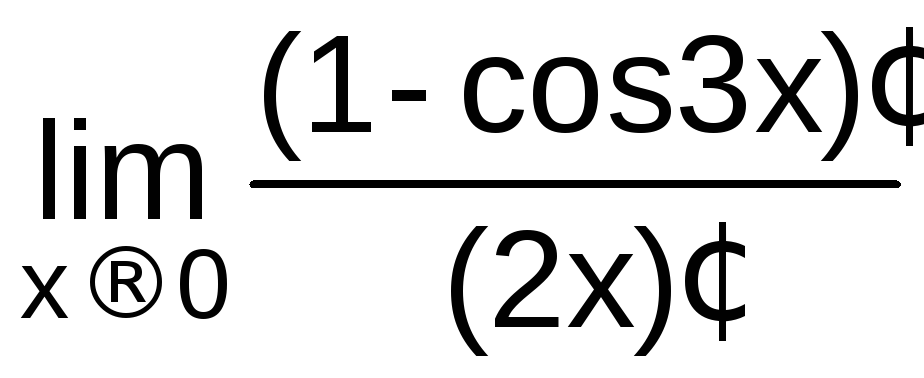
Поскольку функции ,g(x)=2x удовлетворяют условиям теоремы Лопиталя, то ==0.

Замечание 1. Теорема Лопиталя справедлива и в том случае, когда функции ,не определены в точкеx₀, но и.

В самом деле, если доопределить ,, положив, тогда,будут непрерывны в точкеx₀, а потому теорема Лопиталя будет применима к ним.

Замечание 2. Правило Лопиталя применимо и в том случае, когда

, .

Действительно, введя новую переменную , видим, чтоy→0 при x→. Тогда ===.

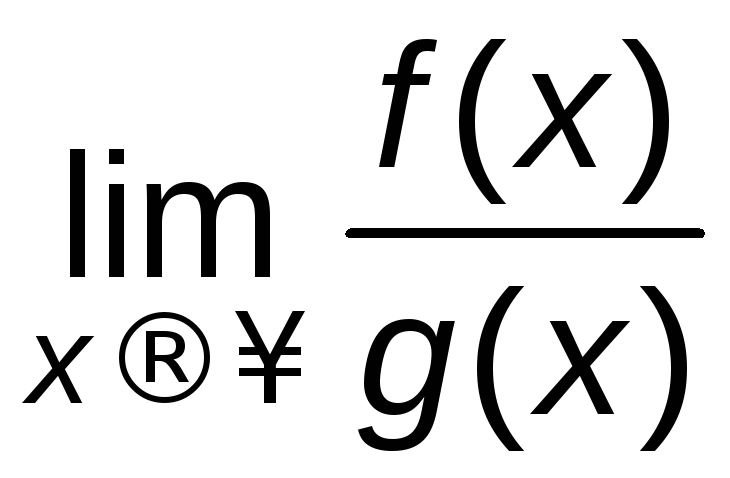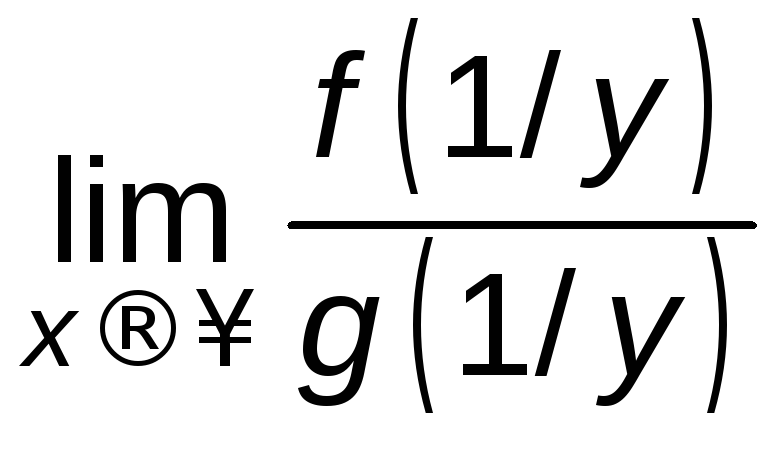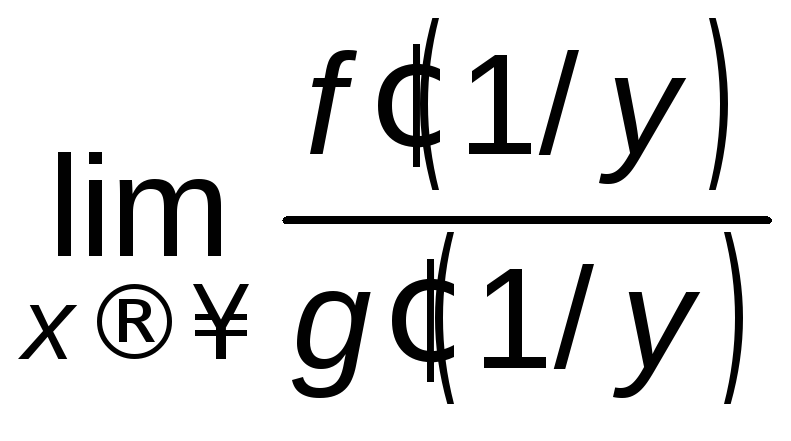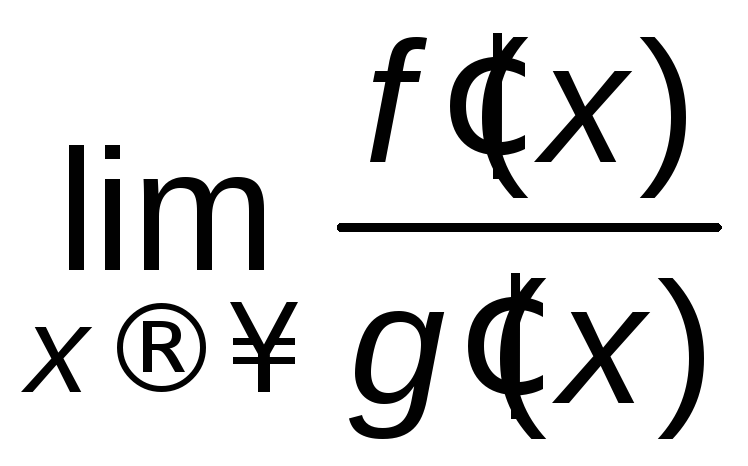Теорема Лопиталя (раскрытие неопределенностей типа ).

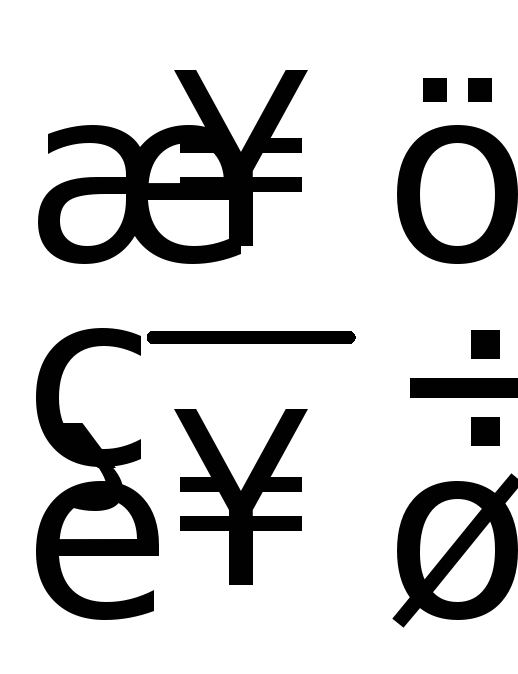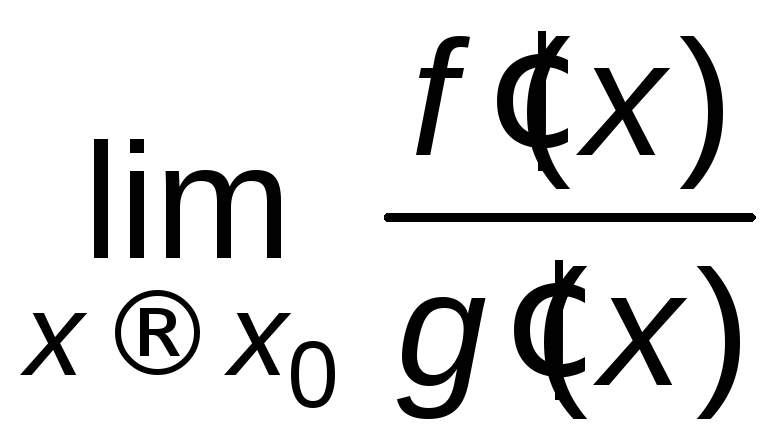Пусть функции ,дифференцируемы в окрестности точкеx₀, за исключением самой точки x₀, причем , и пусть,. Если существуетто существует и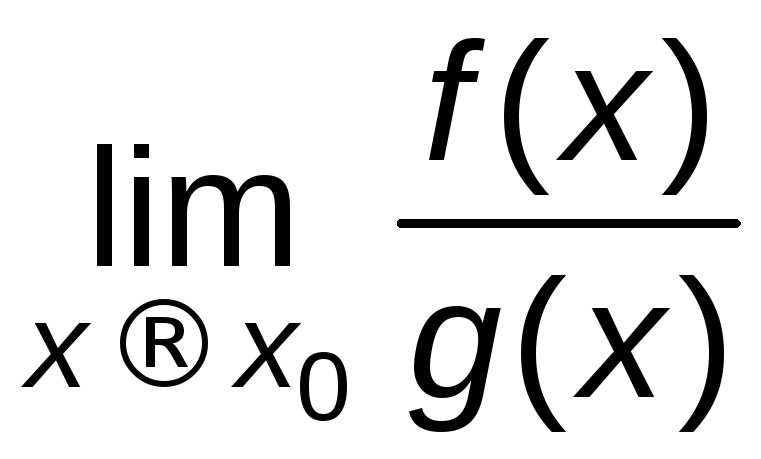, причем

=.

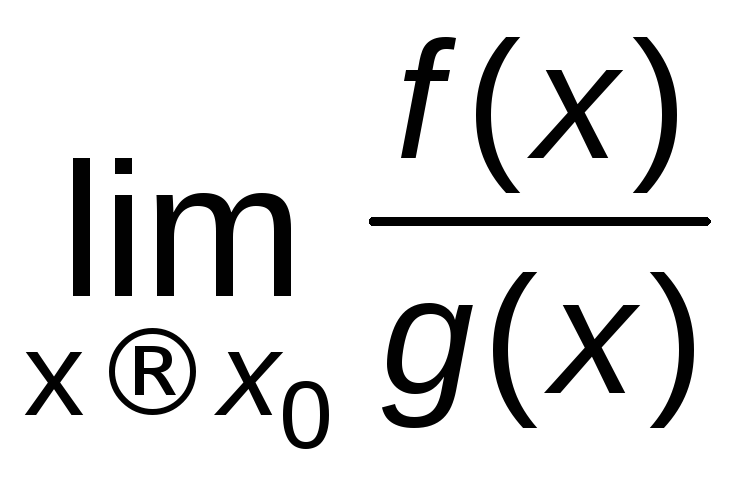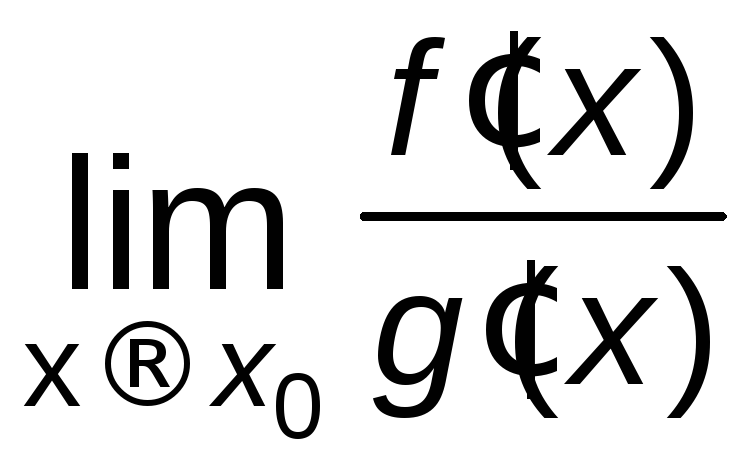Замечание 3. Предел отношения двух функций может существовать, в то время как предел отношения их производных не существует.

Например, =1, а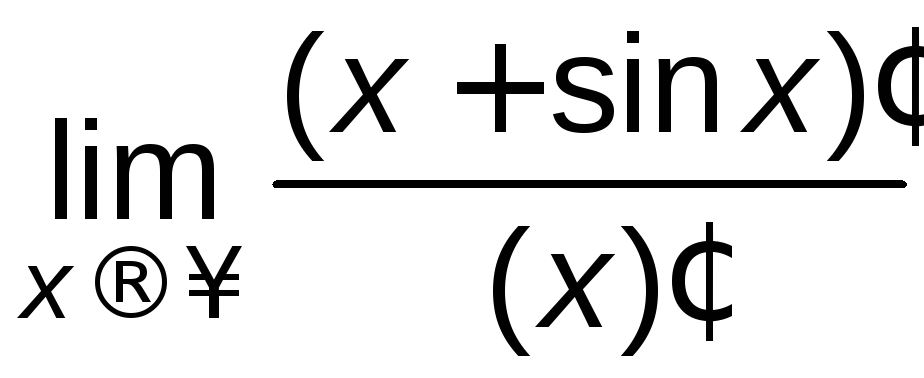=– не существует, так какне существует.

Пример 6.3. Найти .

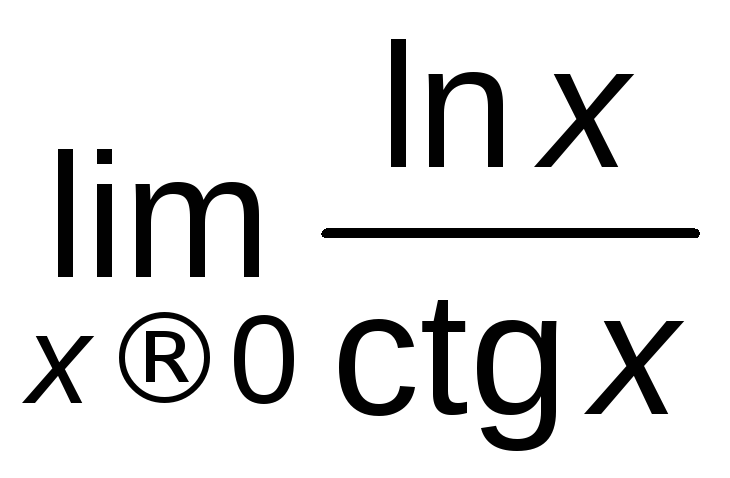Решение.

При x → 0 и x > 0 ,, следовательно, имеем отношение двух бесконечно больших приx→0 и неопределенность типа . Вычислим:

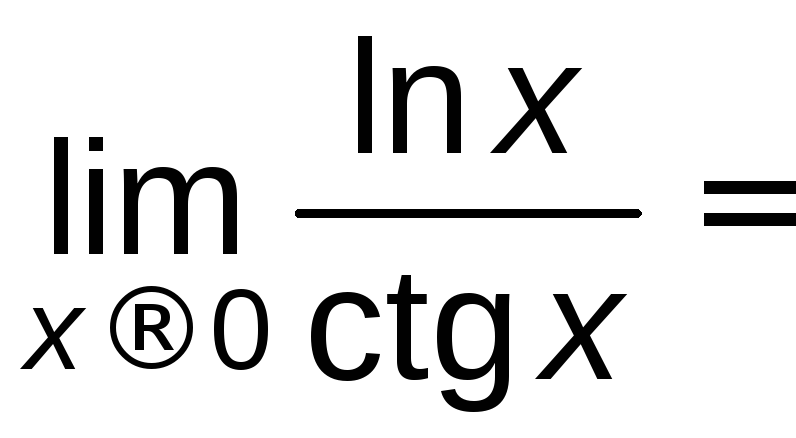
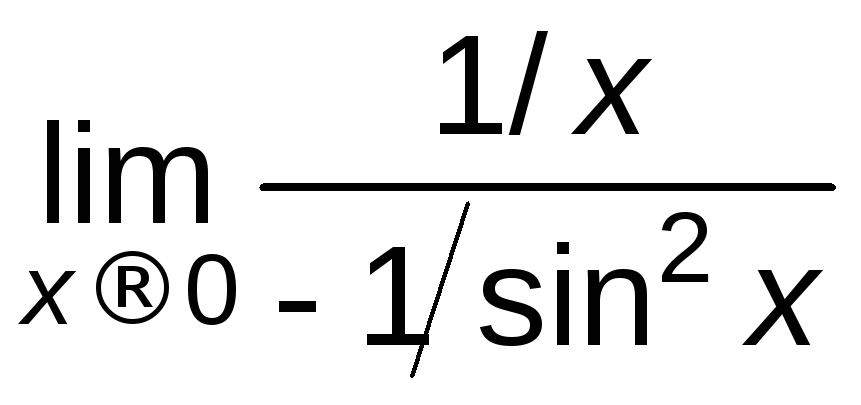= –= –= 0.

Пример 6.4. Найти .

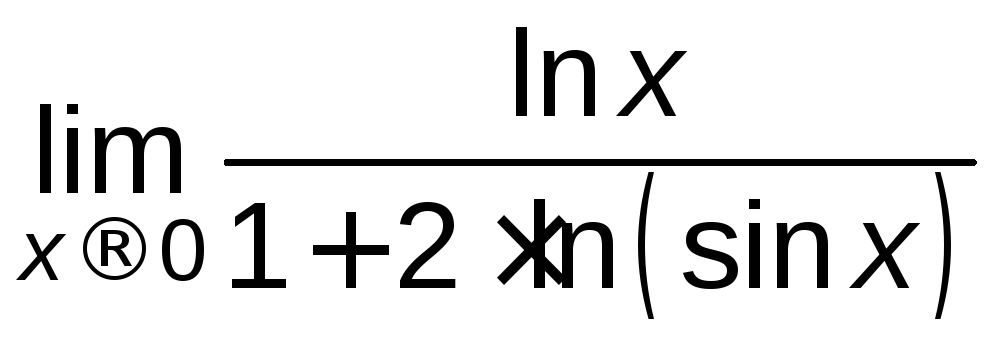Решение.

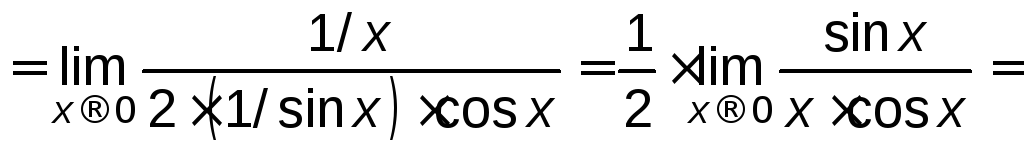
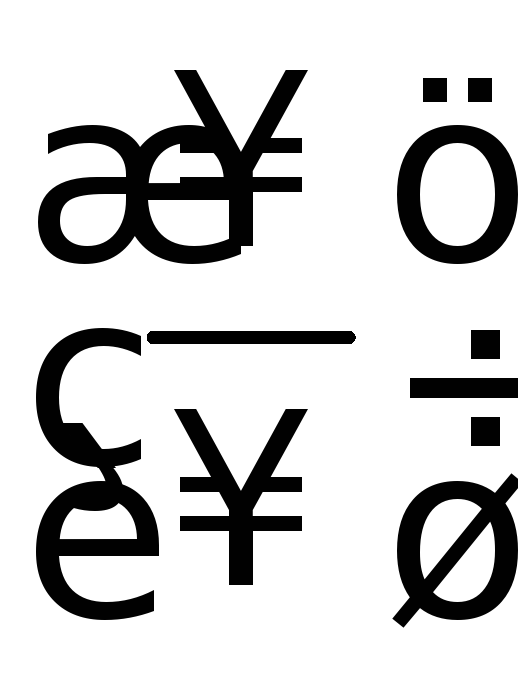Замечание 4. Если приx → x₀ () является неопределенностью типаили, и,g'(x) удовлетворяют условиям теоремы Лопиталя, то

==.

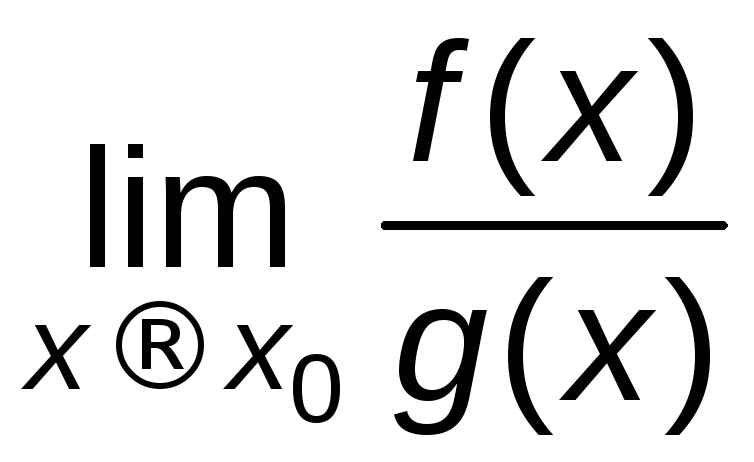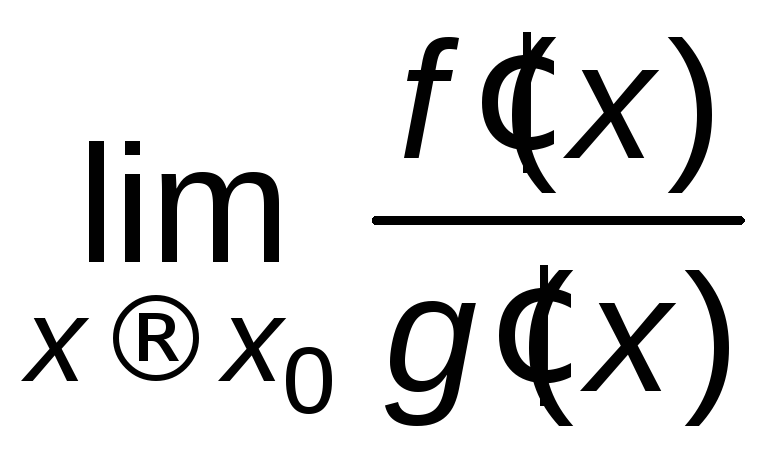Таким образом, для раскрытия неопределенностей типа илииногда приходится применять правило Лопиталя несколько раз.

Замечание 5. Теорема Лопиталя остается верной и тогда, когда =.

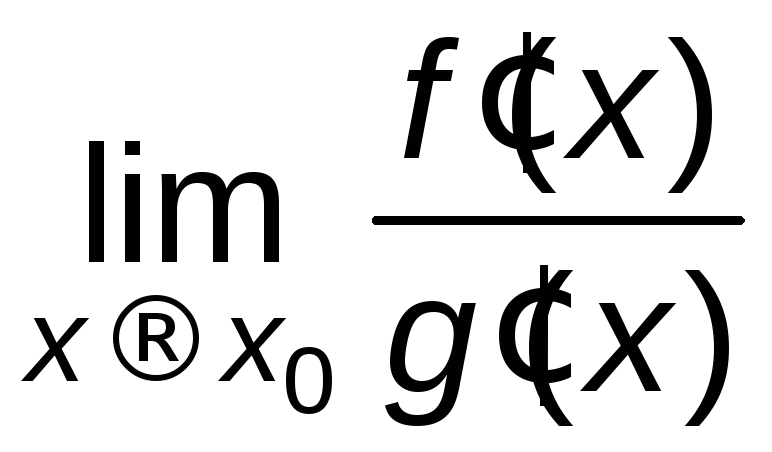Пример 6.5. Найти .

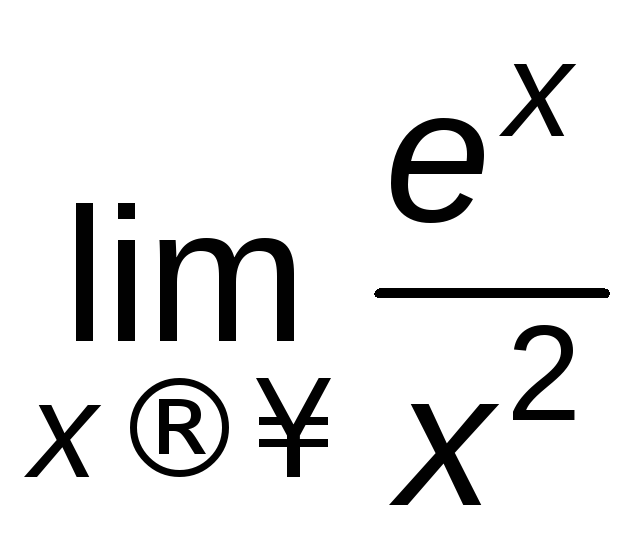Решение.

Имеем неопределенность типа . Применяя теорему Лопиталя два раза, получим:===.

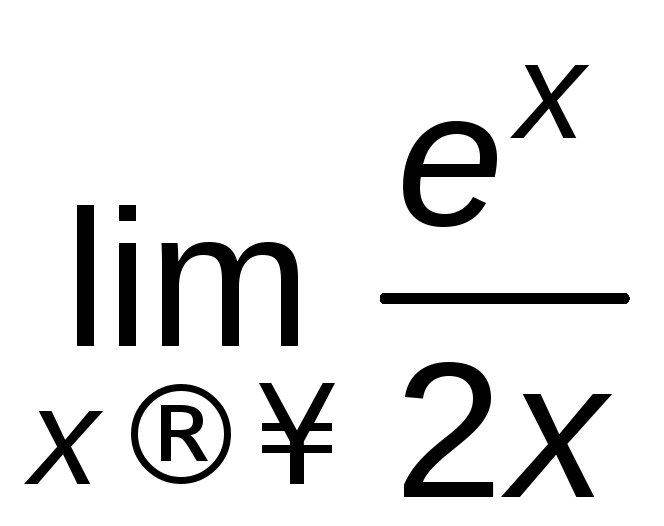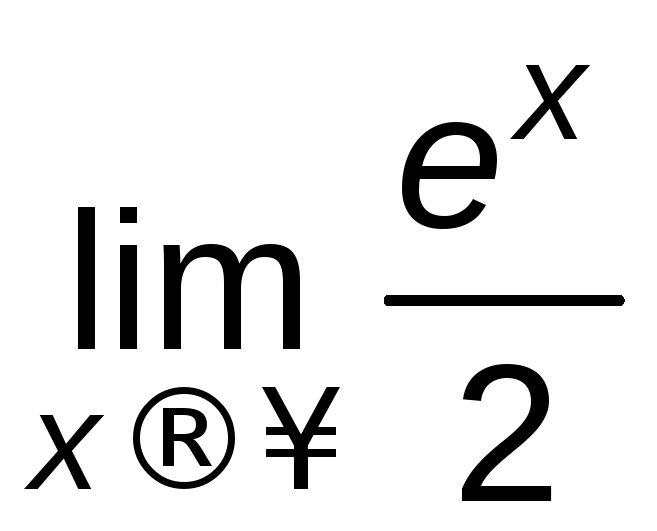Пример 6.6. Найти .

Решение.

Так как , то имеем неопределенность типа (0·). Преобразуем ее к виду :

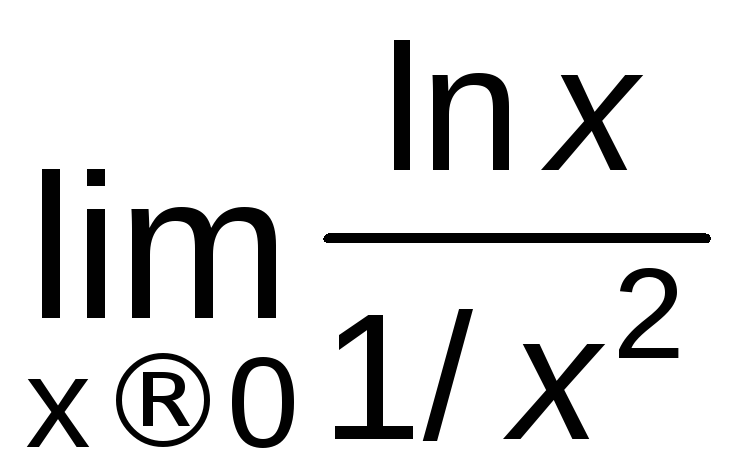=, затем применим правило Лопиталя:

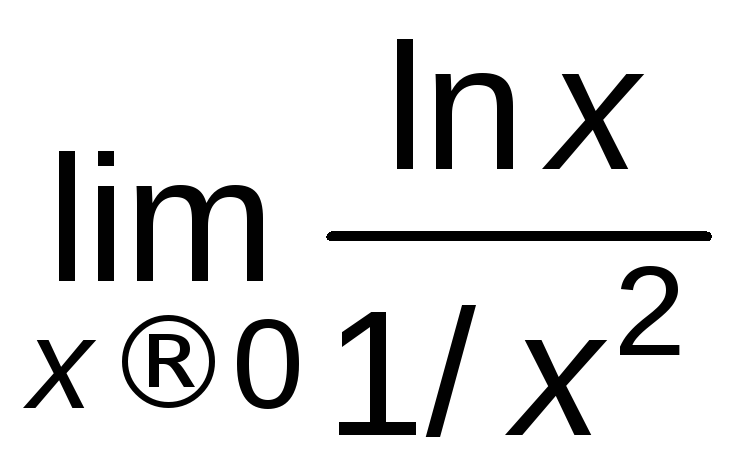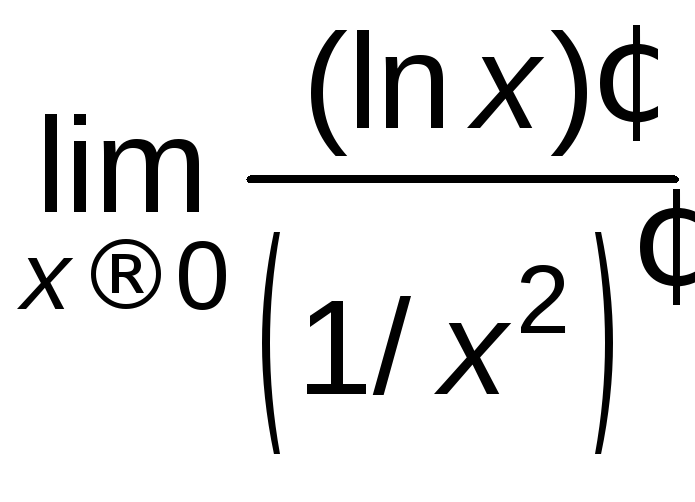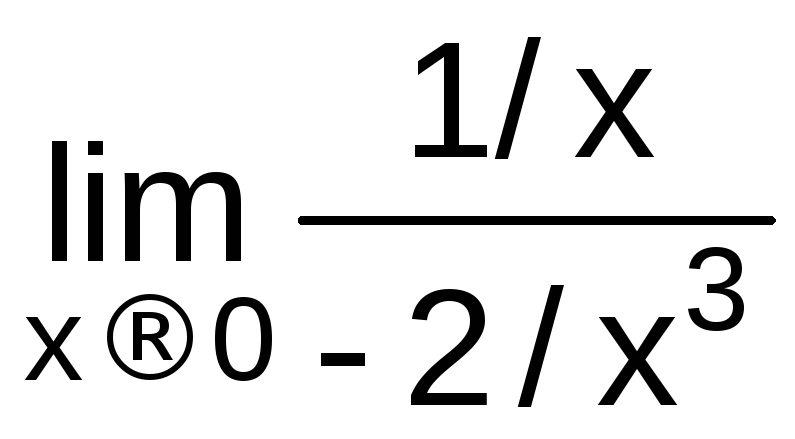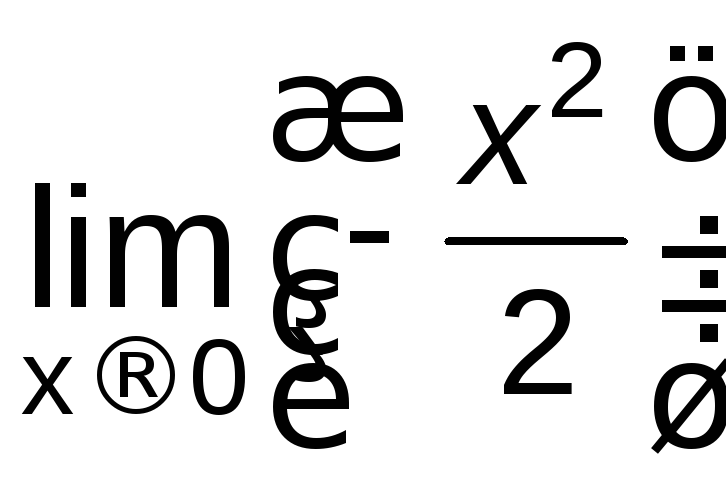====0.

Итак, .

Пример 6.7. Найти

Решение.

.

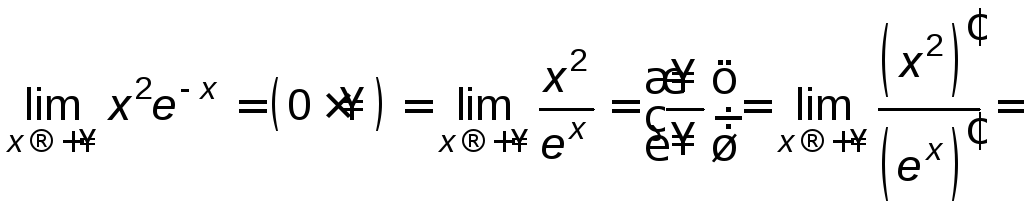
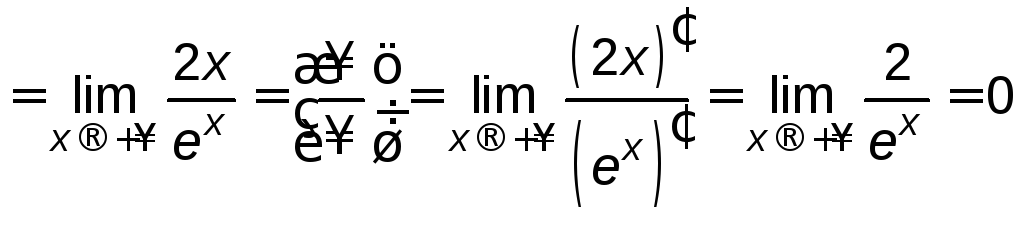Пример 6.8. Найти .

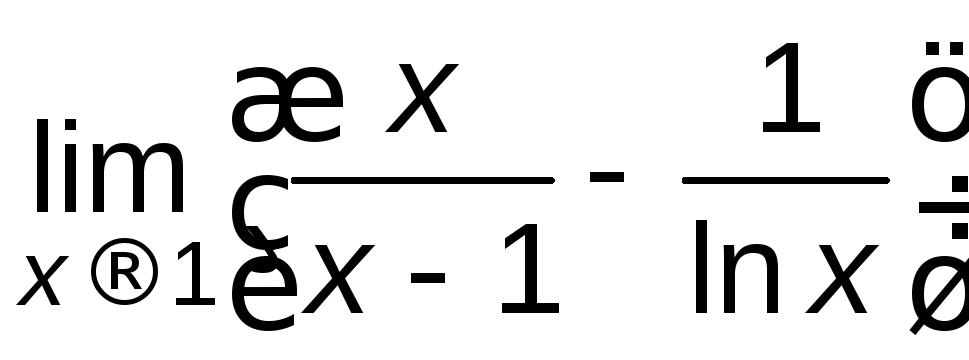Решение.

.

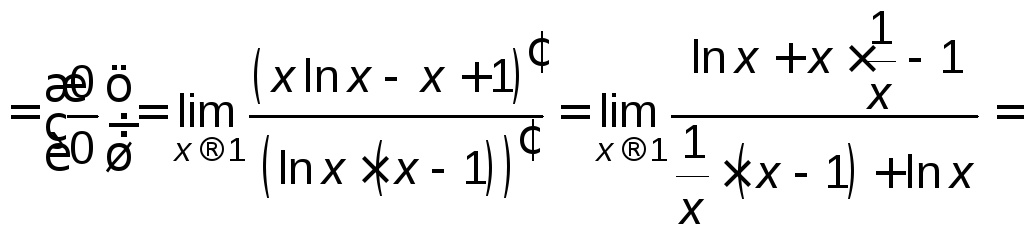
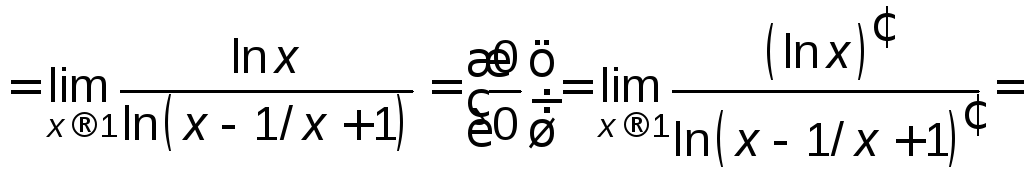
Пример 6.9.Найти.

Решение.

В данном случае имеем неопределенность типа , поэтому для раскрытия этой неопределенности применим метод логарифмирования.

Пусть 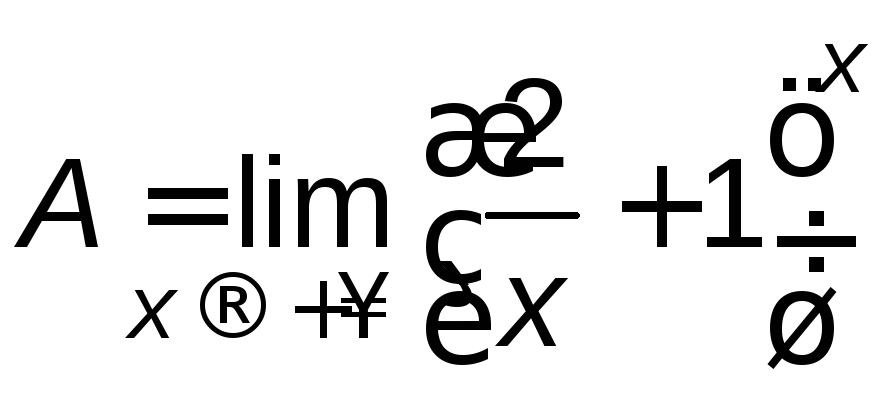. Тогда с учетом того, что логарифмическая функция  непрерывна,  имеем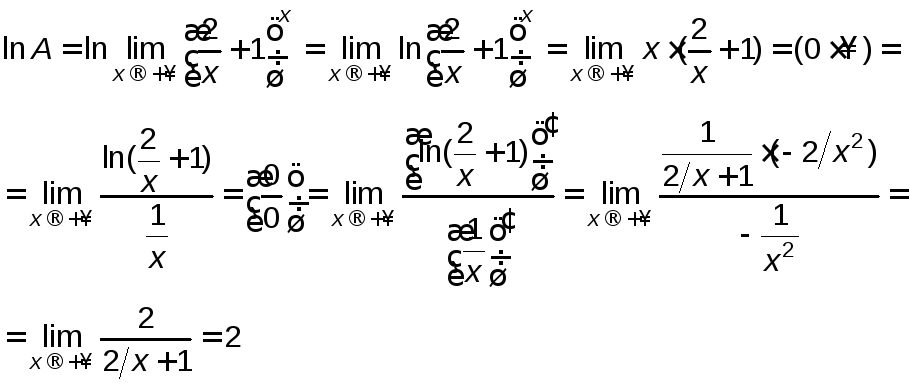

Так как , то.