ман для 1ПМ-11 / 2 курс 2011 / практика / Дослідження функції / практика № 15

Міністерство освіти і науки, молоді та спорту України

Горлівський технікум Донецького національного університету

ПРАКТИЧНЕ ЗАНЯТТЯ № 15

з теми: «Повне дослідження функції. Побудова графіка.»

Модуль КЗН-02. ПР.О.03.06 Дослідження функції

Дисципліна: «Математичний аналіз»

Розглянуто та схвалено Розробив викладач

на засіданні циклової Велікодна О. В.

комісії інформаційних технологій

та прикладної математики.

протокол № 1 від 30.08.2011 р.

Голова циклової

комісії ІТ та ПМ І. П. Сошина

ПЛАН ЗАНЯТТЯ

Дата: курс: ІІ

Викладач: Велікодна Ольга Володимирівна.

Тема: Повне дослідження функції. Побудова графіка функції.

Мета:

• Дидактична: вдосконалювати вміння досліджувати функцію на екстремум, знаходити проміжки монотонності, досліджувати на опуклість, знаходити асимптоти графіка функції та будувати її графік.

• Виховна: підвищити рівень засвоєння навчального матеріалу, розвивати наукове мислення, усне мовлення студентів.

• Методична: вдосконалювати методику проведення практичних занять з використанням технології проблемного та проектного навчання.

Тип: практичне заняття № 15

Вид: практичне заняття – дослідження.

Методи та форми проведення заняття: практичні, дедуктивні, проблемно – пошукові, фронтальна, групова робота.

Наочні посібники: -

Роздавальний матеріал: тестові завдання до актуалізації знань, картки - завдання до самостійного виконання студентами.

Обчислювальні засоби: -

Література:

1. Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.

2. Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.

3. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.

4. Марон А. И. Дифференциальное и интегральное исчисление в примерах и задачах. – М.: Наука, 1973.

ХІД ЗАНЯТТЯ.

1. Організаційна частина:

1. відсутні;

2. підготовка до заняття;

3. перевірка д/з.

2. Мотивація навчальної діяльності студентів:

3. Актуалізація опорних знань:

• Контроль за підготовкою студентів до практичного заняття:

4. Інструктаж щодо виконання практичної роботи.

5. Видача завдань для виконання роботи.

6. Виконання студентами практичної роботи.

7. Оформлення індивідуальних звітів виконаної роботи, захист практичної роботи.

8. Підведення підсумків. Оцінювання.

9. Домашнє завдання:

Конспект практичного заняття № 15.

Тема: «Повне дослідження функції. Побудова графіка.»

Інструктаж до виконання практичного завдання.

Методичні вказівки.

Загальне вивчення функції проводимо за таким планом:

1. Визначити область визначення функції.

2. Визначити відповідну область значень даної функції.

3. Перевірити функцію на парність чи непарність.

4. Перевірити функцію на періодичність.

5. Знайти точки перетину графіку функції з осями координат;

6. Перевірити функцію на неперервність, визначити тип точок розриву, якщо такі є. Перевірити поведінку функції на кінцях області визначення (знайти відповідні границі).

7. Дослідити функцію на монотонність, знайти екстремуми.

8. Дослідити функцію на випуклість, точки перегину.

9. За всіма отриманими даними викреслити графік функції в системі координат.

Приклад виконання практичного завдання.

Провести повне дослідження функції та побудувати її графік.

Розв’язок:

• Область визначення функції D(у) = .

• Функція не є парною, не є непарною, тобто функція загального виду.

• Точок перетину з віссю ОУ немає, з віссю ОХ точка перетину: .

• Точка розриву х = 0, причому , тому х = 0 – точка розриву ІІ роду.

• Так як 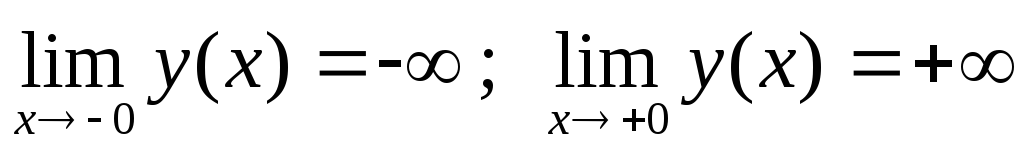, то х = 0 (вісь ОУ) є вертикальною асимптотою. Нахилені асимптоти: у = kх + b , 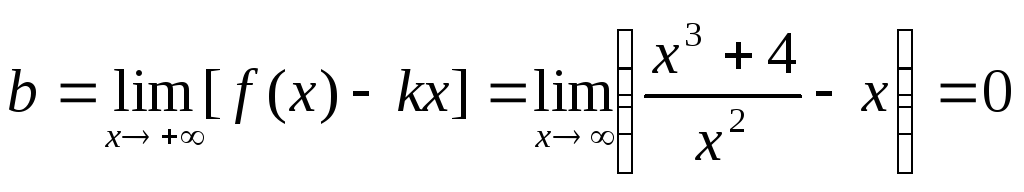. Тому, рівняння нахиленої асимптоти є у = х.

• Екстремуми та інтервали монотонності функції: , у′ = 0 при х = 2, та не існує при х = 0, яка є точкою розриву функції. Точки х = 0 та х = 2 розривають числову пряму на проміжки (-∞, 0), (0, 2), (2, +∞). y′ > 0 в проміжках (-∞, 0) та (2, +∞), y′ < 0 в проміжку (0, 2). Тобто, функція у(х) зростає на проміжках (-∞, 0) та (2, +∞), спадає на проміжку (0, 2). Окрім того, точка х = 2 є точкою мінімуму, у(2) = 3.

• Інтервали випуклості, вгнутості, точки перегину: . y′′ > 0 на всій області визначення функції у і, тому, графік функції вгнутий.

• Користуючись отриманими даними, будуємо графік функції.

Виконати практичне завдання.

Провести повне дослідження функції та побудувати її графік.