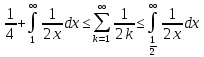Разное / Выпускная Лицей
.docxОЦІНКА СУМИ МОНОТОННОГО РЯДУ
Розглянемо
ряд
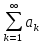 ,
що складається з невід'ємних членів
,
що складається з невід'ємних членів
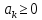 ,
причому
,
причому
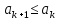 ,
для будь-якого к.
,
для будь-якого к.
Цей ряд можна оцінити за допомогою інтегралу, записавши оцінку в вигляді подвійної нерівності наступним чином
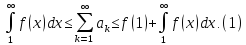
Доведення цієї нерівності обґрунтовується в доведенні інтегральної ознаки збіжності рядів.
Інтегральна ознака збіжності рядів
Якщо
функція f
спадає
на проміжку
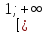 і f(1)=х1,
f(2)=х2,
…, f(к)=хк,
…,
то для збіжності ряду
і f(1)=х1,
f(2)=х2,
…, f(к)=хк,
…,
то для збіжності ряду
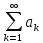 необхідно і достатньо, щоб збігався
інтеграл
необхідно і достатньо, щоб збігався
інтеграл
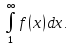
Доведення.
Розглянемо ряд
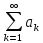 з невід'ємними убуваючими членами
з невід'ємними убуваючими членами
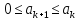 для
будь-якого к
(за умовою) та функцію
для
будь-якого к
(за умовою) та функцію
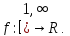 Інтеграл
Інтеграл
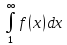 збігається, якщо
збігається, якщо
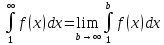 .
Введемо означення Р(b)=
.
Введемо означення Р(b)=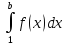 ,
де функція f(x)
невід'ємна.
Якщо розглядати проміжок (b1,
b2)
такий, що b2>b1,
то
,
де функція f(x)
невід'ємна.
Якщо розглядати проміжок (b1,
b2)
такий, що b2>b1,
то
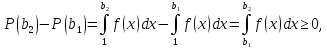
якщо
f(x)≥0.
Тоді отримаємо, що P(b2)≥P(b1),
тобто функція Р зростає. За необхідною
умовою інтегрування інтеграл збігається
тоді, і тільки тоді, коли функція обмежена.
Функція f(x)
спадає на проміжку
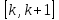 і для неї виконується нерівність:
і для неї виконується нерівність:
f(k+1)≤f(x)≤f(k).
Так як f(k+1)=aк+1, f(k)=ak i k≤x≤k+1, то нерівність перепишеться у такому вигляді
ak+1≤f(x)≤ak.
Користуючись монотонністю інтеграла (за умовою), робимо оцінку інтеграла наступним чином:
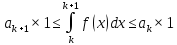
для
будь-якого k=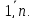
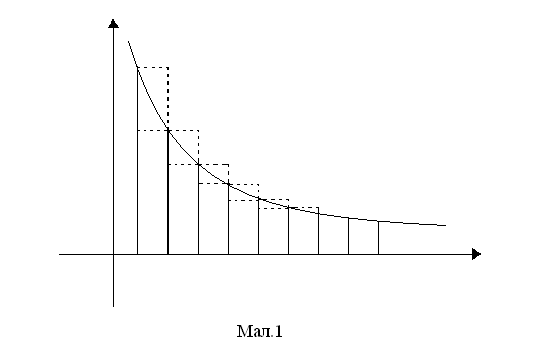
Тут (див. мал. 1):
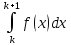 --
це площа підграфіка на проміжку
--
це площа підграфіка на проміжку
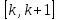 ;
;
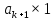 – площа
прямокутника надбудованого над
підграфіком;
– площа
прямокутника надбудованого над
підграфіком;
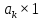 – площа
прямокутника, побудованого нижче
підграфіка.
– площа
прямокутника, побудованого нижче
підграфіка.
Складаючи
ці нерівності при k
від 1 до п,
отримаємо:
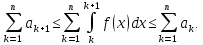
За
означенням часткові сум
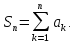
Використовуючи адитивність інтегралу, отримуємо
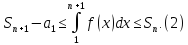
Ряд
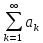 збігається, коли часткові суми
збігається, коли часткові суми
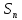 обмежені.
Отже, Р(п+1)=
обмежені.
Отже, Р(п+1)=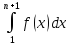 обмежена. Значить, існує границя
обмежена. Значить, існує границя
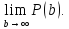 Інтеграл
Інтеграл
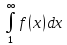 збігається, значить, функція Р(п+1)=
збігається, значить, функція Р(п+1)=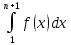 обмежена. Тепер застосовуємо нерівність
(2) і отримуємо, що
обмежена. Тепер застосовуємо нерівність
(2) і отримуємо, що
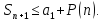 Часткова сума
Часткова сума
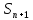 обмежена, і отже ряд
обмежена, і отже ряд
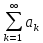 з додатніх членів збігається.
з додатніх членів збігається.
Тобто
ряд
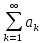 збігається тоді і тільки тоді, коли
збігається інтеграл
збігається тоді і тільки тоді, коли
збігається інтеграл
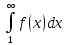 .
.
Доведення завершено.
При
цьому переходячи в нерівності (2) до
границі п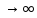 ,
отримаємо оцінку (1).
,
отримаємо оцінку (1).
Також, як видно на мал. 1, оцінка (1) може бути отримана з геометричних міркувань.
Дійсно,
сума ряду
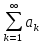 дорівнює сумі площ прямокутників, які
покривають підграфік функції f(х)
на проміжку
дорівнює сумі площ прямокутників, які
покривають підграфік функції f(х)
на проміжку
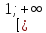 .
В той же час сума ряду
.
В той же час сума ряду
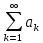 дорівнює сумі площ прямокутників, які
лежать нижче підграфіка функції f(х)
на проміжку
дорівнює сумі площ прямокутників, які
лежать нижче підграфіка функції f(х)
на проміжку
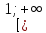 .
Враховуючи, що площа підграфіка функції
f(х)
на проміжку
.
Враховуючи, що площа підграфіка функції
f(х)
на проміжку
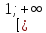 дорівнює
дорівнює
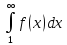 ,
отримаємо нерівність (1).
,
отримаємо нерівність (1).
УТОЧНЕННЯ ОЦІНОК ДЛЯ ОПУКЛИХ ФУНКЦІЙ
Опукла функція та її властивості
Означення. Функція f(х) називається опуклою, якщо множина точок площини, що лежать вище графіка функції f(х), є опуклою.
Означення. Функція f(х) називається опуклою вгору, якщо множина точок, що лежить нижче підграфіка функції f(х), є опуклою.
Очевидно, що:
(а) функція опукла тоді і тільки тоді, коли будь-яка дуга графіку, замкнена між точками a i b, лежить нижче хорди, що з'єднує точки (a, f(a)) та(b, f(b));
(b) функція опукла вгору тоді і тільки тоді, коли будь-яка дуга графіку, замкнута між точками a i b, лежить вище хорди, що з'єднує точки (a, f(a)) та(b, f(b)).
Означення. Диференційована на проміжку функція опукла, якщо її графік лежить не нижче будь-якої дотичної; опукла вгору, якщо її графік лежить не вище будь-якої дотичної.
Означення. Якщо функція двічі диференційована на проміжку (a, b), то, якщо друга похідна функції невід'ємна для будь-якого х з проміжку (a, b), графік функції опуклий донизу, якщо друга похідна функції від'ємна для будь-якого х з проміжку (a, b), то графік функції опуклий вгору.
У
випадку опуклої функції оцінка (1) може
бути посилена:
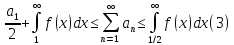
Геометричне доведення
Розглянемо мал. 2.
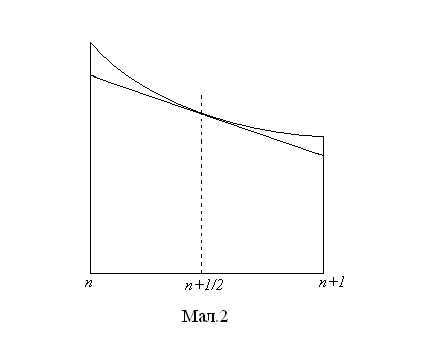
Якщо провести дотичну до графіка функції у середній точці, то площа підграфіка знизу оцінюється через площу трапеції.
Можна побачити, що ця оцінка схожа з формулами приблизного чисельного інтегрування, а саме з методом трапецій і прямокутників.
З мал. 2 видно, що
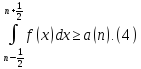
Дійсно
площа трапеції, що знаходиться під
графіком функції f(х)
(див. мал. 2) дорівнює добутку середньої
лінії трапеції на її висоту, тобто
а(п)×1,
а повна площа підграфіка дорівнює
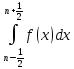 .
.
Додаючи нерівність (4) за к, отримаємо
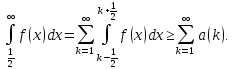
Це є лівою оцінкою нашого ряду.
Розглянемо тепер мал. 3.
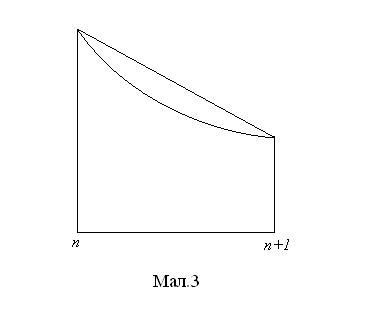
На
ньому трапеція містить підграфік
функції. Тому площа трапеції (рівна
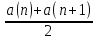 )
перевищує
площу підграфіка, тобто
)
перевищує
площу підграфіка, тобто
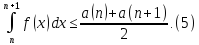
Додаючи нерівність (5) для усіх к, отримуємо
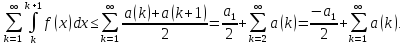
Переносячи
доданок
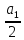 в ліву частину, отримуємо
в ліву частину, отримуємо
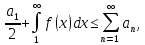
Тобто оцінку нашого ряду зліва.
Аналітичне доведення
Доведемо нерівності (4) і (5) використовуючи властивість (а) опуклих функцій.
Аналітично властивість (а) можна записати наступним чином:
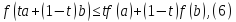
де 0<t<1.
При a=n-x, b=n+x, x=1/2 нерівність (6) отрумує такий вигляд
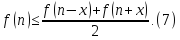
Проінтегрувавши нерівність (7) за х від 0 до ½ отрумаємо нерівність (4).
При a=n, b=n+1, t=x нерівність (6) приймає вигляд
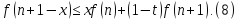
Проінтегрувавши нерівність (8) для х від 0 до 1 отримаємо нерівність (5).
Зауваження
Зауваження 1. Для скінченної суми нерівність (3) приймає вигляд:
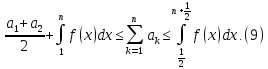
Зауваження 2. Якщо функція випукла вгору, то нерівність (9) змінює знак на протилежний, тобто приймає вигляд:
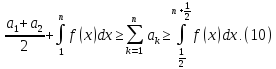
Аналізуючи
нерівності (1) і (3), можна сказати, що
друга оцінка нашого ряду
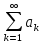 як правило точніша, а саме оцінка суми
ряду
як правило точніша, а саме оцінка суми
ряду
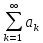 знизу. В той же час оцінка (3) суми ряду
знизу. В той же час оцінка (3) суми ряду
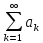 зверху може виявитися гірше, ніж оцінка
(1) суми ряду
зверху може виявитися гірше, ніж оцінка
(1) суми ряду
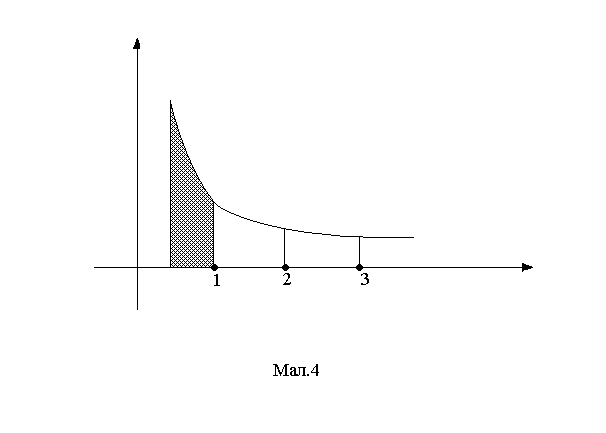
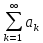 зверху. Це відбувається тоді, коли f(х)
швидко спадає на проміжку (1/2, 1) (див.
мал. 4). Як правило в цьому випадку оцінку
(3) можна зробити точніше оцінки (1) якщо
розглянути суму ряду як суму першого
доданка і залишку ряду:
зверху. Це відбувається тоді, коли f(х)
швидко спадає на проміжку (1/2, 1) (див.
мал. 4). Як правило в цьому випадку оцінку
(3) можна зробити точніше оцінки (1) якщо
розглянути суму ряду як суму першого
доданка і залишку ряду:
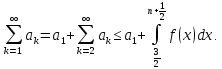
Приклади застосування отриманих оцінок
Приклад 1.
Оцінимо
ряд
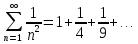
Ряд
є збіжним, оскільки за інтегральною
ознакою
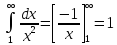 збігається.
Функція f(x)=
збігається.
Функція f(x)=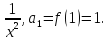 Застосуємо
формулу (1) для оцінки ряду
Застосуємо
формулу (1) для оцінки ряду
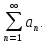
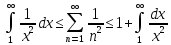
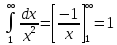
Отримуємо
оцінку 1≤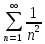 ≤2.
≤2.
Застосовуючи
другу формулу для оцінки ряду
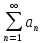 ,
можна переконатися, що друга оцінка
більш точна.
,
можна переконатися, що друга оцінка
більш точна.
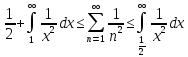
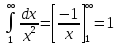
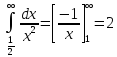
Отримуємо
оцінку
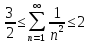 і бачимо, що вона більш точна, ніж оцінка
за допомогою формули (1).
і бачимо, що вона більш точна, ніж оцінка
за допомогою формули (1).
Приклад 2.
Нехай
дано спадаючу геометричну прогресію
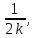 де
к=1,
2, 3… Ряд є збіжним, оскільки за інтегральною
ознакою
де
к=1,
2, 3… Ряд є збіжним, оскільки за інтегральною
ознакою
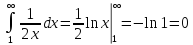 .
.
Тоді оцінимо цей ряд за допомогою формули (1).
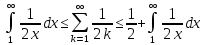
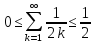
Це оцінка нашого ряду за допомогою формули (1).
Оціними ряд за формулою (3).