
ЭлектрикаОптикаЗадачи2013
.pdf
20
2. ОПТИКА
2.1. Сводка основных формул
Фотометрия
Видимый свет является электромагнитными волнами, длина которых лежит в диапазоне 380 < λ < 760 нм. Энергетические параметры света характеризуются световым потоком, силой света и освещенностью.
Световой поток Φ равен отношение энергии W света, падающего на площадку dS , к промежутку времени t , за который перенесена эта энергия
Φ = W t .
t .
Сила света I , излучаемая точечным источни- |
|
|
n |
|
||||
ком S, равна отношению светового потока |
Φ к те- |
S |
dω |
r α |
S |
|||
лесному углу |
ω (рис. 2.1) |
|
|
|
|
|
Рис. 2.1 |
|
|
I = ΔΦ |
ω. |
|
|
|
|
||
|
|
|
|
|
|
|||
Телесный угол dω равен отношению площадки |
Sn = |
S cosα, перпенди- |
||||||
кулярной направлению света, к квадрату расстояния до источника света |
|
|||||||
|
ω= |
Sn = |
S cosα . |
|
|
|
|
|
|
|
r 2 |
r 2 |
|
|
|
|
|
Освещенность Е равна отношения светового потока, падающего на пер- |
||||||||
пендикулярно |
ориентированную |
площадку |
S к |
величине этой площадки: |
||||
E = ΔΦ S . Для точечного источника освещенность определяется по закону |
|
|||||||
E = |
I cosα |
, |
|
r 2 |
|||
|
|
где I – сила света, r – расстояние от источника света до освещаемой поверхности, α - угол падения света на поверхность.
Геометрическая оптика
Геометрическая оптика рассматривает световые явления в приближении, когда длина волны λ намного меньше размеров предметов. В этом приближении распространение волн описывается лучами – кривыми, перпендикулярными волновым поверхностям. В основу геометрической оптики положены следующие законы:
− прямолинейности (в однородной среде свет распространяется прямолинейно);
− независимости (лучи при пересечении не взаимодействуют); − отражения (угол падения равен углу отражения: α = α′, рис. 2.2);
− преломления (отношение синусов углов падения и преломления равно
относительному показателю преломления второй среды: |
sin α |
= |
n2 |
= n); |
|
sinβ |
n |
||||
|
|
|
|||
|
|
1 |
|
||

|
|
21 |
|
|
|
|
|
− обратимости (при изменении направления на противопо- |
α |
|
α′ |
||||
|
|||||||
ложное, луч света пройдет по той же траектории) . |
n1 |
|
|
||||
Вся геометрическая оптика может быть построена на прин- |
n2 |
|
β |
||||
ципе Ферма: между двумя точками 1 и 2 свет распространяется за |
|
|
|
||||
Рис. 2.2 |
|||||||
минимальное время |
|
|
|
||||
2 |
= 1 |
2 |
2 |
|
|
|
|
t12 = ∫dl |
∫ndl = min , |
L12 = ∫ndl = min . |
|
|
|
||
1 v |
c |
1 |
1 |
|
|
|
|
Здесь L – оптический путь луча света. Законы прямолинейности, отражения, преломления и обратимости выводятся из принципа Ферма.
В плоском зеркале изображение симметрично относительно плоскости зеркала. В сферическом зеркале радиусом R расстояния от предмета до зеркала a и от изображения до зеркала b связаны с фокусным расстоянием f формулой
|
|
1 |
+ 1 |
= |
|
1 |
, f |
= |
R . |
|
|
|
|||
|
|
a |
|
|
|
|
|||||||||
|
|
|
b |
|
|
f |
|
2 |
|
|
|
|
|||
Формула линзы связывает расстояние от предмета а, расстояние до изо- |
|||||||||||||||
бражения b и фокусное расстояние f линзы |
|
|
|
|
|
|
|||||||||
1 |
1 |
1 |
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
, |
|
= (n − |
|
|
|
|
||||||||
a |
+ b = |
|
|
|
|
|
1) |
|
|
+ |
|
, |
|||
|
f |
|
f |
|
R |
|
R |
||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
где n – показатель преломления стекла, R1 и R2 – радиусы кривизны передней и задней поверхностей линзы.
Линейное увеличение β линзы и сферического зеркала равно
β =b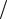 a .
a .
Интерференция света
Когерентными называются волны одинаковой частоты и постоянной разности фаз. При наложении такие волны интерферируют, что проявляется в чередовании светлых и темных полос.
Условия максимума и минимума при интерференции имеют вид
max = ±kλ, |
|
1 |
|
min = ± k + |
2 |
λ, |
|
|
|
|
где λ - длина волны, = L2 − L1 – оптическая разность хода лучей, k = 0, 1, 2…
Для двух когерентных источников света, дающих интерференцию, расстояние между соседними интерференционными полосами равно
x = dl λ,
где d - расстояние между источниками, l – расстояние до экрана.
Оптическая разность хода лучей при интерференции в тонких пленках определяется выражением
= 2d n2 − sin 2 α ± λ2 ,
где d – толщина пленки; α – угол падения; λ - длина волны. Добавка ±λ/2 появляется из-за изменения фазы волны на π при отражении.
|
22 |
|
|
|
|
|
Радиус темного кольца Ньютона в отраженном свете или светлого кольца в |
||||||
проходящем свете равен |
|
|
|
|
|
|
rk = |
kRλ, |
|
|
|
|
|
где R –радиус кривизны линзы, λ - длина волны, k = 0, 1, 2...- номер кольца. |
|
|||||
Дифракция света |
|
|
|
bi+1 = bi +λ/ 2 |
||
Дифракцией называется отклонение света от |
|
|
||||
|
|
bi |
|
|
||
прямолинейного распространения и загибание в |
|
|
|
|
||
|
|
|
|
|
||
область геометрической тени, которое наблюдает- |
S |
a |
O |
b |
P |
|
ся, когда длина волны λ сравнима с размерами |
|
|
|
|
|
|
преграды. Дифракция описывается принципом |
|
|
|
|
|
|
Гюйгенса – Френеля. Для упрощения расчетов |
|
|
Рис. 2.3 |
|
|
|
широко применяют метод зон Френеля. Зоны Фре- |
|
|
|
|
|
|
неля строят так, чтобы расстояние от соседних зон отличалось на λ/2 и волны |
||||||
от соседних зон были в противофазе (рис. 2.3). Радиус зоны Френеля под номе- |
||||||
ром i определяется выражением |
|
|
|
|
|
|
r = i ab λ ,
i |
a +b |
|
где а и b – расстояния от источника S и от точки Р до фронта волны O. Амплитуда колебаний в методе зон Френеля складывается по формуле
|
A |
|
A |
|
|
A |
|
|
A |
|
|
A |
|
A = |
1 |
+ |
1 |
− A |
+ |
3 |
|
+ |
3 |
− A |
+ |
5 |
... |
|
|
|
|
|
|||||||||
|
2 |
2 |
2 |
|
2 |
|
2 |
4 |
|
2 |
|
||
|
|
|
|
|
|||||||||
Условие минимума при дифракции на узкой щели имеет вид b sin ϕ = ±kλ,
где b – ширина щели, ϕ - угол наблюдения темной полосы, k – номер полосы, λ
-длина волны.
Вдифракционной решетке проявляются два явления: дифракция на отдельной щели и интерференция от одинаковых щелей. Условие максимума интерференции для дифракционной решетки имеет вид
d sin ϕ = ±kλ,
где d –расстояние между щелями (период решетки), k – порядок спектра. Угловая дисперсия дифракционной решетки определяется выражением
D |
= dϕ |
= |
k |
= |
k |
. |
ϕ |
dλ |
|
d cosϕ |
|
d 2 − k 2λ2 |
|
Линейная дисперсия характеризует линейный разброс лучей и равна
Dl = ddxλ .
Разрешающая способность решетки определяется выражением
R = λ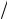 λ = kN ,
λ = kN ,
где N – количество щелей решетки.
Дифракция рентгеновских лучей на кристаллах, которые для них представляют дифракционную решетку, описывается формулой Вульфа – Брегга

23
d sin θ = kλ,
где d – расстояние между атомами, θ - угол скольжения, отсчитываемый от плоскости, в которой расположены атомы.
Поляризация и поглощение света
Интенсивность I плоско поляризованного света, прошедшего через поляризатор, определяется законом Малюса
I = I0 cos2 ϕ,
где I0 – интенсивность падающего света, ϕ - угол между плоскостью колебаний света и плоскостью поляризатора.
Естественный свет неполяризованный, но при отражении и преломлении поляризуется. Закон Брюстера определяет угол падения θБр, при котором отражённый свет полностью поляризован
tg θБр = n1 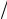 n2 .
n2 .
Интенсивность света при прохождении через вещество уменьшается вследствие его поглощения по закону Бугера
I = I0 e−χl ,
где χ - коэффициент поглощения, l – толщина слоя вещества.
Тепловое излучение
Все тела при любой температуре поглощают и излучают энергию. Абсолютно чёрным называют тело, которое поглощает полностью любое падающее на него излучение. Энергетическая светимость Re (энергия, излучаемая за еди-
ницу времени с единицы поверхности) абсолютно чёрного тела определяется законом Стефана – Больцмана
Re = σT 4 ,
где σ = 5,67 10−8 Вт м2 К4 - постоянная Стефана – Больцмана; T- абсолютная температура. Полная энергия равна W = SRe , где S - площадь поверхности тела.
м2 К4 - постоянная Стефана – Больцмана; T- абсолютная температура. Полная энергия равна W = SRe , где S - площадь поверхности тела.
Длина волны λm , которой соответствует максимум излучательной способ-
ности абсолютно чёрного тела, связана с температурой законом смещения Вина
λm = b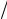 T ,
T ,
где b = 0,29 10-2 м К постоянная Вина.
Квантовая оптика
Энергия фотона определяется формулой Планка
ε = hν,
где h = 6,63 10-34 Дж с – постоянная Планка, ν - частота света.
Формула Эйнштейна для фотоэффекта выражает закон сохранения энергии hν = A + mv2 2 ,

24
где А – работа выхода электрона из металла, mv2  2 - кинетическая энергия вы-
2 - кинетическая энергия вы-
летевшего электрона.
Изменение длины волны λ рентгеновских лучей в эффекте Комптона
λ = mch (1 − cosθ),
m – масса электрона, с – скорость света в вакууме, θ - угол рассеяния.
Атомная физика
При переходе электрона в атоме с одной орбиты на другую, атом излучает или поглощает фотон с энергией
hν = En − Em ,
где n и m – номера орбит, En и Em - энергии электрона на этих орбитах.
Число атомов N радиоактивного вещества, которое распадается за время t, определяется формулой радиоактивного распада
N = N0e−λt ,
где N0 - начальное число атомов, λ - постоянная радиоактивного распада, которая связана с периодом полураспада Т выражением T = ln 2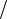 λ.
λ.
Энергия связи ядра определяется соотношением
E = mc2 ,
где m - дефект массы, который определяется по формуле m = Zmp + (A − Z )mn − m0 ,
где Z – порядковый номер изотопа (количество протонов), А – массовое число (количество протонов и нейтронов), mp и mn - масса протона и нейтрона,
m0 = mA − Zme - масса ядра, равная разности масс атома mA и электронов Zme .
2.2. Примеры решения задач
1. Лампа, подвешенная к потолку, дает в горизонтальном направлении силу света I = 60 кд. Какой световой поток падает на картину площадью S = 0,5 м2 , висящую вертикально на стене в r = 2 м от лампы, если на противоположной стене находится большое зеркало на расстоянии a = 2 м от лампы?
Решение. Как следует из условия задачи на картину К падает световой по-
ток Φ1 непосредственно от лампы Л и световой поток |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
Φ2 , отраженный от зеркала З (рис. 2.4). Общий световой |
|
|
К |
|
Л |
|
|
З |
||||
|
|
|
|
|||||||||
поток равен их сумме: Φ = Φ1 + Φ2 . Световой поток, па- |
|
|
|
Ф1 |
|
|
|
|||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||
дающий на поверхность S , |
связан с силой света соотно- |
|
|
|
|
|
|
|
|
|
||
|
|
|
r |
Ф2 |
a |
|||||||
шением |
|
|
|
|
|
|
||||||
|
I |
|
|
|
|
|
Рис. 2.4 |
|
|
|
||
Φ = ∫ |
|
dS , |
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
||
S |
|
r |
|
|
|
|
|
|
|
|
|
|
где r - расстояние от источника света до элемента поверхности dS . В нашем случае размеры картины гораздо меньше расстояния r и интегрирование дает
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
Φ1 |
= |
I |
S |
, Φ2 = |
I S |
|
|
. |
|
|
|
|||
|
|
|
|
|
r 2 |
|
|
|
|
|
(r + 2a)2 |
|
|
|
|
||
Здесь 2a + r - расстояние, которое проходит от лампы до картины, отразившись |
|||||||||||||||||
от зеркала. Окончательно имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
Φ = Φ1 + Φ2 |
|
|
|
+ |
|
2 |
|
= 8,34 лм. |
|
|
|
||||
|
|
= I S |
|
2 |
(r + 2a) |
|
|
|
|
||||||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|||
|
2. Луч света падает под углом α = 30° на плоскопараллельную стеклянную |
||||||||||||||||
пластинку и выходит из нее параллельно первоначальному лучу. Показатель |
|||||||||||||||||
преломления стекла n = 1,5. Какова толщина d пластинки, если расстояние ме- |
|||||||||||||||||
жду лучами l = 1,94 см? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Решение. Ход лучей в пластине изображен на рис. 2.5. |
α |
|
|
|||||||||||||
Толщину пластинки найдем из |
АВС: |
|
|
|
|
|
|
|
|
||||||||
|
|
|
d = AB = ACcosβ, |
|
|
(1) |
A |
|
|
||||||||
где β - |
угол преломления, который определим из закона |
d |
β |
D |
|||||||||||||
преломления |
sinβ =sin α n , |
|
|
|
|
B |
C |
l |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
где n - показатель преломления стекла. Сторону АС найдем |
Рис. 2.5 |
|
|||||||||||||||
из |
АСD по формуле |
|
|
CD |
|
|
l |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
AC = sin CAD = sin(α −β). |
|
|
|
|||||||||||
|
Подставляя полученные выражения в (1), после тригонометрических пре- |
||||||||||||||||
образований найдем толщину пластины |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
l cosβ |
|
|
|
|
|
|
|
l |
|
|
= 10 см. |
|
|
|
|
|
d = sin(α −β) |
= |
|
|
|
|
− |
|
cosα |
|
|
|
|
|||
|
|
|
|
|
sin α 1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
n2 −sin2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|||
|
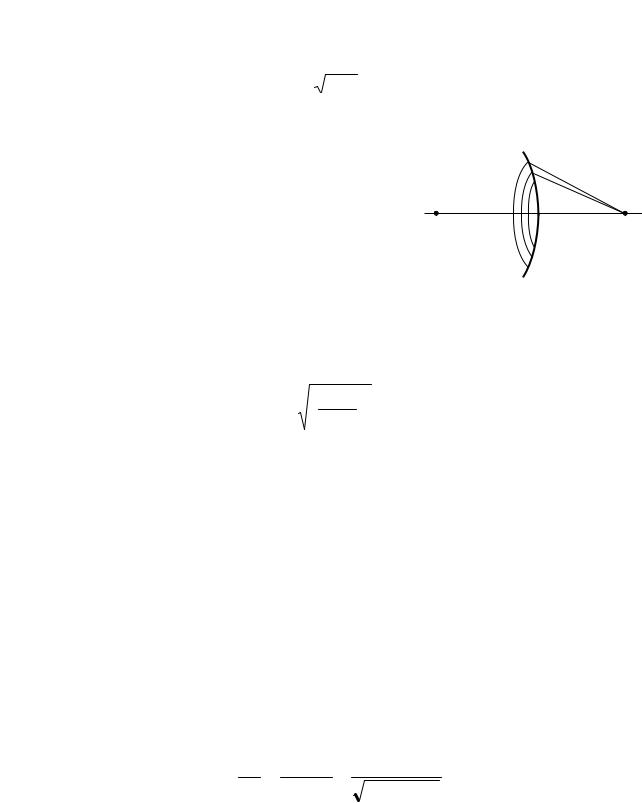
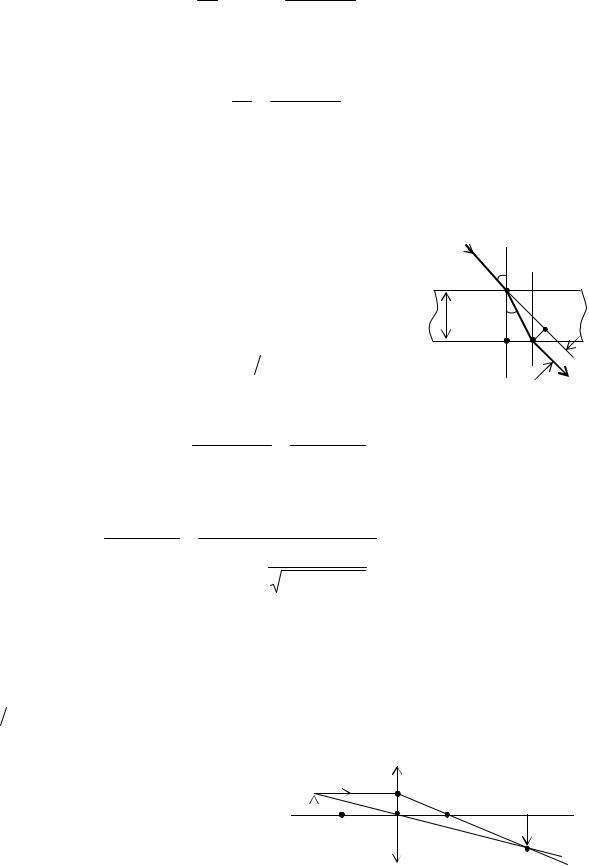
3. На расстоянии а1 = 15 см от двояковыпуклой линзы, оптическая сила кото- |
||||||||||||||||
рой D = 10 диоптрий, поставлен перпендикулярно к оптической оси предмет вы- |
|||||||||||||||||
сотой в h = 2 см. Найти положение и высоту изображения. Построить чертеж. |
|
||||||||||||||||
|
Решение. Фокусное расстояние линзы найдем по ее |
оптической |
си- |
||||||||||||||
ле: f =1 D = 10 см. Расстояние от предмета до линзы a1 = 15 см, т.е. предмет на- |
|||||||||||||||||
ходится между фокусом и двойным фокусом. Изображение предмета A2 B2 |
по- |
||||||||||||||||
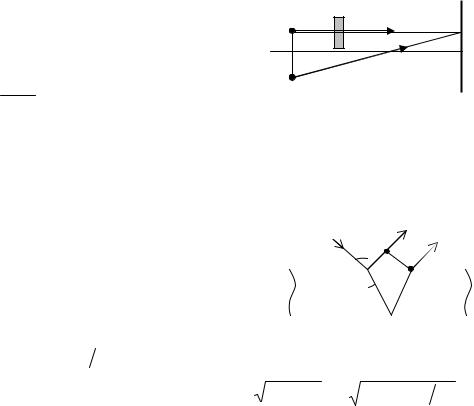
строим, |
используя |
характерные |
лучи: |
|
|
|
|
|
|
|
|||||||
A1O проходит через центр линзы и не |
A1 |
|
|
C |
F2 |
B2 |
|
||||||||||
преломляется, A1 С проходит параллель- |
B1 |
|
F |
O |
|
||||||||||||
|
|
|
|
||||||||||||||
но оптической оси, а после преломления |
|
|
|
|
|
A2 |
|
||||||||||
идет через задний фокус F |
(рис. |
2.6). |
|
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Рис. 2.6 |
|
|
|
Лучи пересекаются в т. А2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Из формулы линзы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
26 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
+ |
1 |
|
= |
|
1 |
, |
|
||||
|
|
|
|
|
|
a |
|
a |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
f |
|
|||||
находим положение изображения |
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
a1 f |
|
|
|
|
|
|
|
|
||||||||
|
|
a2 = |
|
|
|
= 0,3 м. |
||||||||||||
|
|
a1 − f |
||||||||||||||||
|
|
|
|
|
|
|
|
А1В1О и А2В2О: |
||||||||||
Размеры изображения найдем из подобия |
|
|||||||||||||||||
|
y1 |
= |
y2 |
|
→ y |
|
|
= y |
|
|
a2 |
=4 см. |
||||||
|
a |
|
|
|
|
|
||||||||||||
|
|
a |
2 |
|
|
|
|
2 |
|
|
1 a |
|
||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||
4. В опыте Юнга на пути одного из интерферирующих лучей помещалась тонкая стеклянная пластинка, вследствие чего центральная светлая полоса смещалась в положение, первоначально занятое пятой светлой полосой (не считая центральной). Луч падает на пластинку перпендикулярно. Показатель преломления пластинки n = 1,5, длина волны λ = 6 10 −7 м. Какова толщина h пластинки?
Решение. Опыт Юнга, описанный в задаче, изображен на рис. 2.7, где на |
|||||||||
пути луча 1 поставлена стеклянная пластинка. При внесении пластинки оптиче- |
|||||||||
ский путь этого луча увеличится на |
= h(n −1), поэтому интерференционная |
||||||||
картина сместится. Смещение на k |
полос соответствует |
дополнительной раз- |
|||||||
ности хода |
= kλ. |
Приравнивая |
эти |
выражения, |
|
|
|
||
получаем уравнение |
|
|
|
|
S1 |
n |
1 |
|
|
|
h(n −1)= kλ, |
|
|
|
|
||||
|
|
|
|
|
|
||||
откуда находим толщину пластинки |
|
d |
|
2 |
l |
||||
|
h = |
kλ |
|
= 6 мкм. |
|
S2 |
|
|
|
|
|
|
|
|
|
||||
|
n − |
1 |
|
|
|
Рис. 2.7 |
|
||
|
|
|
|
|
|
|
|||
5. На мыльную пленку с показателем преломления n = 1,33 падает белый свет под углом α = 45°. При какой наименьшей толщине пленки h отраженные лучи будут окрашены в желтый цвет ( λ = 6 10−5 см)?
Решение. При отражении света от пленки возни- |
|
|
|
|
2 |
||||||||
|
|
|
|
||||||||||
кает интерференция потому, что лучи 2 и 2′ , отражен- |
|
|
α |
D |
|||||||||
1 |
2′ |
||||||||||||
ные от верхней и нижней поверхностей пленки прохо- |
|
|
|||||||||||
|
|
A |
|
C |
|||||||||
дят разные пути и приобретают разность хода. Из |
|
n |
β |
||||||||||
|
|
|
|||||||||||
рис. |
2.8 |
видно, |
что разность |
хода |
лучей |
будет |
|
|
|
|
|
||
= L2 |
− L1 = 2АB – AD, где L1 и L2 - оптические пути |
|
|
|
B |
|
|||||||
лучей. Из |
ABC находим AB = h cosβ, где β- угол пре- |
|
|
Рис. 2.8 |
|||||||||
|
|
|
|
|
|||||||||
ломления. По закону преломления |
sin α |
= n и cosβ = 1 −sin2 β = |
1 −sin2 α n2 . |
||||||||||
|
|||||||||||||
|
|
|
|
sinβ |
|
|
|
|
|
|
|
||
Из |
АСD |
находим оптический |
путь |
луча |
2: |
L1 = AC sin α = |
|||||||
= 2AB sinβ sin α. Окончательно для оптических путей лучей получим |
|
||||||||||||
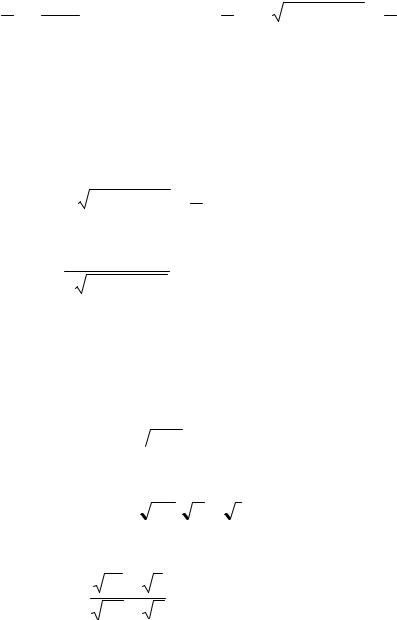
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L = |
2h |
sinβ sin α; L = |
2h |
|
n . |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
cosβ |
2 |
cosβ |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Оптическая разность хода лучей после преобразований будет |
|
|
|
||||||||||||||
= L |
|
+ |
λ |
= |
2h |
(n −sin α sinβ) − |
λ |
= |
2h n |
2 |
−sin |
2 |
α − |
λ |
. |
(1) |
|
− L |
|
cosβ |
2 |
|
|
2 |
|||||||||||
2 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
В выражении (1) для луча 2 добавлена разность хода λ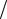 2 , т.к. при отраже-
2 , т.к. при отраже-
нии от оптически более плотной среды происходит изменение фазы на π, что эквивалентно дополнительному пути λ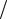 2 . Для луча 2' такое не наблюдается.
2 . Для луча 2' такое не наблюдается.
Максимум интерференции наблюдается при условии = kλ, где k = 0,1, 2 … . Минимальная толщина пленки будет при k = 0 для первого максимума, таким образом с учетом (1) получаем уравнение
2h |
n2 |
−sin2 α − |
λ |
= 0 , |
|
откуда находим толщину пленки |
|
|
2 |
|
|
λ |
|
|
|
||
h = 4 |
|
= 0,13 мкм. |
|||
n2 |
−sin2 α |
||||
6. Найти расстояние l2 между третьим и шестнадцатым темными кольцами Ньютона, если расстояние l1 между вторым и двадцатым темными кольцами равно 4,8 мм. Наблюдение проводится в отраженном свете.
Решение. Радиус k - го темного кольца при наблюдении в отраженном свете определяется формулой
rk =  kRλ,
kRλ,
где R – радиус кривизны линзы. Расстояние между кольцами с номерами i и k (k > i) найдем по формуле
lki |
= rk − ri = |
Rλ( k − i ). |
(1) |
||
Используя формулу (1), найдем расстояние между 3 и 16 кольцами, зная |
|||||
расстояние между 2 и 20 кольцами: |
|
|
|||
l |
|
=l |
16 − |
3 =3,66 мм. |
|
|
2 |
1 |
20 − |
2 |
|
7. На дифракционную решетку нормально падает пучок света. Угол дифракции для натриевой линии с длиной волны λ1 = 589 нм в спектре первого порядка был найден равным α1 = 17°8'. Некоторая линия дает в спектре второго порядка угол дифракции, равный α2 = 24°12'. Найти длину волны λ2 этой линии и число штрихов t на 1 мм решетки.
Решение. Из условия максимума для дифференциальной решетки d sin ϕ= 2λ для первой и второй линий имеем
d sin ϕ1 = λ1, d sin ϕ2 = 2λ2 .
Решая эти уравнения относительно d и λ2 , получим
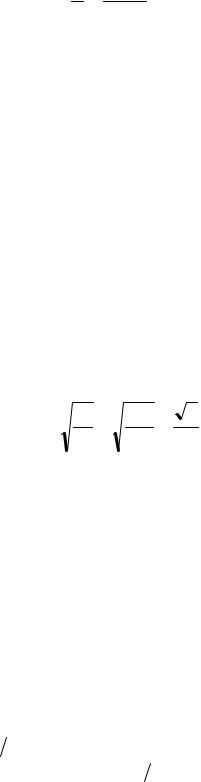
|
|
|
|
|
28 |
|
|
|
λ |
|
= λ |
|
sin ϕ2 |
= 400 нм, |
d = |
λ1 |
. |
2 |
1 2sin ϕ |
|
||||||
|
|
|
|
sin ϕ |
||||
|
|
|
1 |
|
|
1 |
|
|
Количество штрихов t решетки на единицу длины обратно периоду d решетки
t = 1 = sin ϕ1 d λ1
8. Найти угол ϕ между главными плоскостями поляризатора и анализатора, если интенсивность естественного света, проходящего через поляризатор и анализатор, уменьшается в 4 раза.
Решение. Естественный свет не поляризован, в нем направления колебаний ориентированы произвольно. Поляризатор пропускает колебания только в одном направлении и на выходе поляризатора будет линейно поляризованный свет с колебаниями вдоль плоскости поляризатора. Разложим колебания естественного света интенсивности I0 по двум направлениям: вдоль и поперек плоскости поля-
ризатора. Через поляризатор пройдут только продольные колебания. Поэтому интенсивность I1 прошедшего через поляризатор света будет в два раза меньше:
I1 = I0 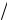 2. Далее этот поляризованный свет проходит через анализатор. Интенсивность I2 прошедшего света определяется законом Малюса
2. Далее этот поляризованный свет проходит через анализатор. Интенсивность I2 прошедшего света определяется законом Малюса
I2 = I1 cos2 ϕ,
где ϕ - искомый угол между плоскостями поляризатора и анализатора. Отсюда с учетом условия задачи находим
cosϕ= |
I2 |
= |
2I2 = |
2 |
, ϕ = 45°. |
|
I1 |
|
I0 |
2 |
|
9. Мощность излучения абсолютно черного тела N = 10 кВт. Найти величину излучающей поверхности S тела, если максимум спектральной плотности его энергетической светимости приходится на длину волны λm = 7 10-5 см.
Решение. По закону Стефана-Больцмана энергетическая светимость абсолютно черного тела равна
R = σT 4 . |
(1) |
e |
|
Эта величина определяет мощность излучения с единицы поверхности. Мощность излучения с поверхности S равна: N = RэS . Отсюда можно найти пло-
щадь излучающей поверхности
S = |
N |
. |
(2) |
|
|||
|
R |
|
|
|
e |
|
|
Из закона Вини λm =b T находим температуру излучающего тела |
|
||
T =b λm , |
(3) |
||
где λm - длина волны, на которую приходится максимум излучения, b - посто-
янная Вина.
Подставляя (3) и (1) в (2) получим

29
S = |
Nλ4m |
2 |
|
= 6 см . |
|
σb4 |
10. Найти постоянную Планка h, если известно, что электроны, вырываемые из металла светом с частотой ν1 = 2,2 1015 Гц, полностью задерживаются разностью потенциалов U1 = 6,6 В, а вырываемые светом с частотой ν2 = 4,6 1015 Гц - разностью потенциалов U2 = 16,5 В.
Решение. Для решения задачи воспользуемся уравнением Эйнштейна для фотоэффекта
hν = A + mv2 2 ,
где hν - энергия фотона, А – работа выхода электрона, mv2 2
энергия выбитого электрона. Чтобы затормозить выбитые электроны, надо совершить работу eU , где U - задерживающее напряжение. Для разных частот света на основании (1) имеем
hν1 = A + eU1 , hν2 = A + eU2 .
Отсюда, исключив работу А, находим постоянную Планка
h= e(U1 −U2 ) = 6,62·10-34 Дж·с.
ν1 − ν2
11.Какую энергию W можно получить от деления массы m = 2 г урана 23592U , если при каждом акте распада ядра урана выделяется энергия Q = 200
МэВ?
Решение. Чтобы найти энергию, которая выделится при распаде ядер урана, найдем количество атомов урана N в данной массе вещества по формуле
N = mμ N A ,
где N A = 6,02 1023 моль-1 – число Авогадро, μ = 0,235 кг/моль – молярная масса
урана.
Зная количество распавшихся ядер урана, найдем полную энергию
W =QN =Q mμ N A =1,64 1011 Дж = 4,55 104 кВт час.
Это очень большая энергия. Для сравнения, чтобы получить такую же энергию, надо сжечь 5,5 т угля, т.е. в 2,7 миллиона раз больше по массе.
2.3. Задачи для работы в аудитории
1. Свет от электрической лампочки с силой света I = 200 кд падает под углом α = 45° на рабочее место, создавая освещенность Е = 141 лк. На каком расстоянии r от рабочего места находится лампочка? На какой высоте h от рабочего места она висит?
