
ЭлектрикаОптикаЗадачи2013
.pdf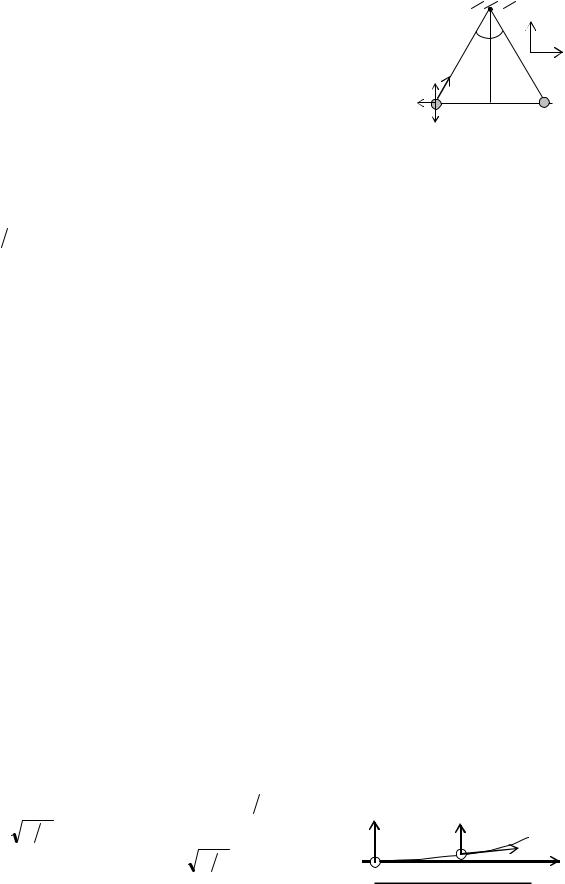
|
|
|
|
10 |
|
|
|
|
|
Решение. На каждый из шариков действуют силы: тяжести mgG, натяжения |
|||||||||
нити T , Кулона FK и Архимеда FA |
(рис. 1.2). Под действи- |
|
|
|
|
|
|||
ем этих сил шарик находится в равновесии, условие кото- |
|
|
|
|
y |
||||
|
|
|
|
||||||
|
|
|
|
||||||
рого имеет вид |
|
G |
|
|
|
|
|
|
|
G |
|
|
|
|
2α |
||||
|
|
|
|
|
|||||
|
mq |
+ FK +T + FA |
= 0. |
|
|
|
|
x |
|
Спроектировав эти силы на оси x |
и |
y , получим следую- |
FA |
TG |
|||||
щие уравнения: |
T cosα − FK = 0, |
FA +T sin α − mg = 0. |
FK |
mgG |
|||||
|
|
|
Рис. 1.2 (1) |
||||||
По закону Кулона и Архимеда имеем:
|
F = k |
q2 |
, F |
=ρ |
Vg = |
ρ |
k |
m |
g , |
|
(2) |
||||||
|
|
|
|
|
|
|
|||||||||||
|
|
К |
εr2 |
|
A |
|
k |
|
|
|
ρ |
|
|
|
|
||
где q = q0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 - заряд каждого шарика, который распределился между шариками |
|||||||||||||||||
поровну, |
r = 2l sin α - расстояние между шариками, ρk |
|
и ε- плотность и отно- |
||||||||||||||
сительная диэлектрическая проницаемость керосина, |
ρ,m и V - плотность, мас- |
||||||||||||||||
са и объем шарика. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Плотность шарика найдем из второго уравнения (2) |
|
|
|||||||||||||||
|
|
|
|
|
ρ = |
ρk mg . |
|
|
|
|
|
|
(3) |
||||
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
Из уравнений (1) и (2) найдем силу Архимеда |
|
|
|
|
q2 |
|
|||||||||||
|
F = mg −T sin α = mg − F tg α = mg − k |
|
tg α. |
||||||||||||||
|
|
|
|||||||||||||||
|
A |
|
|
|
|
К |
|
|
|
|
|
|
εr 2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
После подстановки в (3), получим выражение для плотности |
|||||||||||||||||
|
|
|
|
ρk mg |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
ρ = |
|
|
|
|
|
|
|
|
= 4200 кг/м . |
|
||||||
|
mg − k |
|
q2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
tg α |
|
|
|
|
|
|
|
|||||
|
|
ε(2l sin α)2 |
|
|
|
|
|
|
|
||||||||
3. Электрон с некоторой начальной скоростью v0 влетает в плоский конденсатор параллельно пластинам на равном расстоянии от них. К пластинам конденсатора приложена разность потенциалов U = 300 В. Расстояние между пластинами d = 2 см, длина конденсатора l =10 см. Какова должна быть предельная начальная скорость v0 электрона, чтобы электрон не вылетел из конденсатора?
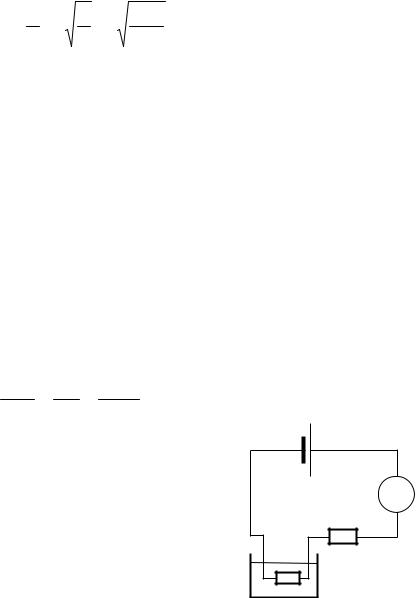
Решение. На электрон при движении между пластинами конденсатора действует электрическая сила F = eE , направленная перпендикулярно пластинам, где E =U d - напряженность электрического поля (рис. 1.3). Двигаясь в
d - напряженность электрического поля (рис. 1.3). Двигаясь в
этом направлении с ускорением |
a = e E m , электрон достигнет пластины за |
|||||
время t = d a . За это время он пролетит вдоль у |
FG |
|
+ |
|
||
1 |
|
|
|
|
v |
|
пластин расстояние x1 = v0t1 = v0 |
d |
a . Траекторией |
|
|
||
|
|
|
х |
|||
электрона будет парабола. Если |
x1 |
<l , то электрон |
- |
|
||
не вылетит из конденсатора. Из этого неравенства |
Рис. 1.3 |
|||||
|
|
|
|
|||
11
находим ограничение для скорости
v0 |
< l |
=l |
a |
=l |
eU |
|
t |
|
d |
|
md 2 |
|
1 |
|
|
|
|
4. Элемент с ЭДС ε = 1,1 В и внутренним сопротивлением r = 1 Ом замкнут на внешнее сопротивление R = 9 Ом. Найти силу тока в цепи, напряжение U R во внешней цепи и напряжение Ur внутри элемента. С каким КПД η рабо-
тает элемент?
Решение. Из закона Ома для замкнутой цепи найдем силу тока
I = |
ε |
= 0,11 А. |
(1) |
|
R + r |
||||
|
|
|
Напряжение UR на внешней цепи и Ur внутри элемента найдем из закона Ома для участка цепи
U R = IR = |
εR |
= 0,99 В, |
Ur = Ir = |
εr |
=0,11 В. |
(2) |
|
R + r |
R + r |
||||||
|
|
|
|
|
КПД источника тока найдем по отношению полезной мощности IUR к затра-
ченной Iε:
η= IUIεR =UεR = RR+ r = 0,9.
Здесь U R и ε определены из формулы (1) и (2).
ε
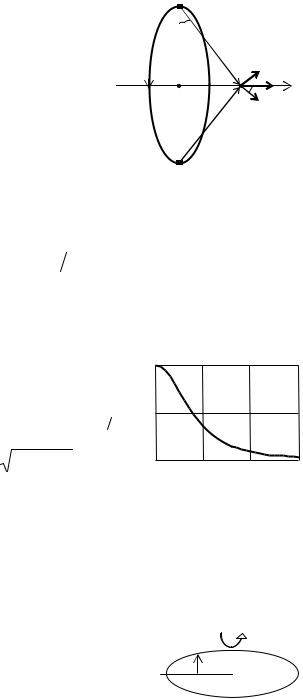
5. В схеме на рис. 1.4 батарея с ЭДС ε = 120 В, |
A |
|
R 2 = 10 Ом, В — электрический чайник. Амперметр пока- |
||
R2 |
||
зывает I = 2 А. Через сколько времени закипит V = 0,5 л |
||
|
||
воды, находящейся в чайнике при начальной температуре |
R1 |
|
t0 = 4° С? Сопротивлением батареи и амперметра пренеб- |
В |
|
речь. КПД чайника η = 76 %. |
||
|
||
Решение. Мощность нагревателя определим по закону |
Рис. 1.4 |
|
Джоуля-Ленца |
||
|
|
|
P = I |
2 R . |
|
(1) |
|
1 |
1 |
|
|
|
Сопротивление нагревателя определим из закона Ома для замкнутой цепи |
|
||||
I = |
ε |
→ R = |
ε − R = 50 Ом. |
|
|
|
|
||||
|
1 |
I |
2 |
|
|
|
R1 + R2 |
|
|
||
Время нагревания воды τ1 найдем из уравнения теплового баланса, которое с учетом КПД нагревателя имеет вид
ηP1τ1 = cm(tк −t0 ), |
(2) |
где с = 4200 Дж/кг м3 - теплоемкость воды, m =ρV - масса воды, ρ =1000 кг/м3 - плотность, tк =100o C - температура кипения. Из уравнения (2) с учетом (1) получим
τ = |
cρv(tк −t0 ) |
|
≈22 мин. |
|
|
||||
1 |
ηI |
2 R |
|
|
|
|
|||
|
|
1 |
|
|
12
6. Найти распределение индукции магнитного поля вдоль оси кругового витка диаметром D = 10 см, по которому течет ток силой I = 10 А. Построить примерный график этой зависимости с нанесением масштаба.
Решение. Для расчета воспользуемся законом Био-Савара-Лапласа и принципом суперпозиции. Выделим на витке два симметрично расположенных
элемента dl и |
dl′ |
(рис. 1.5.). По закону Био-Савара- |
|
|
|
dl |
|
|
|
||||||||||||||||
Лапласа |
|
|
|
|
μ0 I[dl ,rG] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
G |
, |
|
|
|
|
|
|
|
|
R |
α |
dB |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
dB = |
4π |
|
r3 |
|
|
|
dB и dB′, ко- |
I |
|
r |
dBΣ |
||||||||||||
эти элементы создают поля с индукцией |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
O |
x |
|
α |
x |
||||||||||||||||||
торые в силу симметрии направлены под одинаковыми |
|
|
′ |
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
углами к оси х. Поэтому их сумма будет направлена |
|
|
|
r′ |
dB |
|
|
||||||||||||||||||
вдоль этой оси. Отсюда следует, что круговой виток в |
|
|
|
|
|
|
|
||||||||||||||||||
силу симметрии создает магнитное поле, индукция ко- |
|
|
|
dl′ |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
торого направлена вдоль оси х. Этот факт существенно |
|
|
Рис. 1.5 |
|
|
|
|||||||||||||||||||
упрощает решение задачи. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Проекцию |
dB |
на ось |
|
х |
найдем |
|
по |
формуле |
|
|
|
|
|
|
|
||||||||||
dBx = dBcosα. Учитывая, что |
r |
dl , |
|
cosα = R r , получим выражение для |
|||||||||||||||||||||
проекции |
|
|
|
|
|
|
|
|
|
μ0 |
|
IR dl |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
dB |
x |
= |
|
. |
|
|
|
|
|
|
|
(1) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
4π |
|
r3 |
|
|
|
|
|
|
|
|
|
|||||
Индукцию В найдем, проинтегрировав (1) по длине B |
|
|
|
|
|
|
|||||||||||||||||||
контура |
|
μ0 IR |
|
|
μ0 IR2 |
|
|
μ0 |
IR2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
B = ∫dBx = 4π |
|
|
∫l |
dl = |
2 |
|
= |
|
|
|
. |
|
|
|
|
|
|
|
|||||||
r3 |
r3 |
2 |
|
(R2 + x2 )3 2 |
|
|
|
|
|
|
|
||||||||||||||
Здесь при преобразованиях учтено, что r = |
R2 + x2 . |
|
0 |
|
R |
2R x |
|||||||||||||||||||
График этой зависимости приведен на рис. 1.6. |
|
|
|||||||||||||||||||||||
|
|
|
Рис. 1.6 |
|
|
||||||||||||||||||||
7. В магнитном поле, индукция которого равна В = 0,05 Тл, вращается стержень длиною l = 1 м (рис. 1.7). Ось вращения, проходящая через один из концов стержня, параллельна силовым линиям магнитного поля. Найти магнитный поток Φ, пересекаемый стержнем при каждом обороте.
Решение. Магнитный поток определяется выражением |
|
|
|
||
G G |
S . |
За один |
O1 |
|
ω |
|
|||||
Φ = ∫BdS . По условию задачи B = const и B |
G |
|
l |
||
оборот стержень очерчивает круг площадью S = πl 2 |
, как по- |
B |
|
||
|
|
|
|||
казано на рис. 1.7. Тогда для потока получим |
|
|
O2 |
|
|
Φ = Bπl2 =0,15 Вб. |
|
|
|
|
|
|
|
Рис. 1.7 |
|||
|
|
|
|||
8. Электрон, ускоренный разностью потенциалов U = 1000 В, влетает в однородное магнитное поле, перпендикулярное направлению его движения. Индукция магнитного поля B = 1,19 10 −3 Тл. Найти радиус R кривизны траектории

13
электрона, период T обращения его по окружности, момент импульса L электрона.
Решение. При ускорении электрона электрическое поле совершает работу A = eU , которая идет на сообщение ему кинетической энергии mvср2  2. При-
2. При-
равнивая выражения, найдем скорость электрона v = 2eU m . |
|
= e[vG, B]. По II |
|
В магнитном поле на электрон действует сила Лоренца FG |
|||
закону Ньютона движение электрона описывается уравнением |
Л |
|
|
|
|
||
maG = e[vG, B]. |
G |
|
G |
Сила Лоренца перпендикулярна v и B . По условию v |
B и магнитное |
||
поле однородное. Поэтому электрон будет двигаться по окружности с ускорением a = v2  R . Такое движение описывается уравнением
R . Такое движение описывается уравнением
m v2 = evB . R
Отсюда найдем радиуса орбиты электрона
R = mveB =9 см.
Момент импульса электрона найдем по формуле L = mvR =1,5·10-24кг·м-2/с. Период обращения электрона найдем, наделив длину окружности (путь) на
скорость: T = 2πvR = 2eBπm
трона не зависит от его скорости.
9. В цепь переменного тока напряжением U = 220 В включены последовательно емкость С, резистор R и индуктивность L. Найти напряжение U R на ре-
зисторе, если известно, что напряжения на конденсаторе UC = 2UR , а на индуктивности U L =3U R . Определить сдвиг фаз ϕ между током и напряжением и
мощность Р в цепи для R = 100 Ом.
Решение. По закону Ома для переменного тока имеем
I = UZ , Z =  R2 + (X L − XC )2 , (1)
R2 + (X L − XC )2 , (1)
где Z - полное сопротивление, R , X C и X L активное, емкостное и индуктивное
сопротивления отдельных элементов цепи.
При последовательном соединении через все элементы цепи протекает одинаковый ток. Напряжения на отдельных элементах найдем согласно закону Ома найдем по формулам
U R = IR , UC = I XC , U L = I X L . |
(2) |
Отсюда с учетом условия задачи UC = 2U R и U L =3U R определим сопротивления конденсатора, катушки и полное сопротивление цепи
X C = 2R , X L =3R , Z =  2R .
2R .
Из уравнений (1) и (2) найдем силу тока в цепи и напряжение на резисторе

|
|
|
14 |
I = U |
= |
U , |
U R = IR = U = 156 В. |
Z |
|
2R |
2 |
Сдвиг фаз между током и напряжением найдем по формуле
tg ϕ = |
X L − X C |
= 1, ϕ = 45°. |
|
||
|
R |
|
Мощность определим по закону Джоуля-Ленца для переменного тока
P = IU cosϕ= U 2 cosϕ = 242 Вт.  2R
2R
1.3. Задачи для работы в аудитории
1. В центре квадрата, в вершинах которого находится по заряду q = 2,33 нКл, помещен отрицательный заряд q0. Найти величину этого заряда, если результирующая сила, действующая на каждый заряд, равна нулю.
Ответ: q0 = -2,23 нКл.
2. Два небольших шарика одинакового радиуса и массы подвешены на нитях так, что их поверхности соприкасаются. После сообщения шарикам заряда q0 = 0,4 мкКл они оттолкнулись друг от друга и разошлись на угол 2α = 60°. Найти массу шариков m, если расстояние от точки подвеса до центра каждого шарика l = 20 см.
Ответ: m = 15,6 г.
3.Медный шарик диаметром d = 1 см помещен в масло. Плотность масла
ρ= 0,8 103 кг/м3. Чему равен заряд шарика q, если в однородном электрическом поле шарика оказался взвешенным в масле? Электрическое поле направлено вертикально вверх и его напряженность E = 3,6 МВ/м.
Ответ: q = 11 нКл.
4.Кольцо радиусом R = 3 см заряжено равномерно зарядом q = 2 нКл.
Найти |
напряженность электрического поля на оси кольца на расстоянии |
||||
x = 4 см от его центра. Построить примерный график зависимости Е(х). |
|
||||
Ответ: E = |
qx |
= 5,8 103 В/м . |
Е |
|
|
4πε0 (x2 + R2 )3 2 |
|
х |
|||
5. |
Шарик |
массой в m = |
40 мг, заряженный |
положительным |
зарядом |
q = 1 нКл, движется со скоростью v = 10 см/с. На какое минимальное расстояние r может приблизиться шарик к положительному точечному заряду q0 = 1,33 нКл?
Ответ: r = 6 см.
6. В плоском горизонтально расположенном конденсаторе, расстояние между пластинами которого d = 10 см, находится заряженная капелька массой m = 5 10-11 г. При отсутствии электрического поля капелька вследствие сопротивления воздуха падает с некоторой постоянной скоростью. Если к пластинам конденсатора приложено напряжение U = 600 В, то капелька падает вдвое мед-

15
ленней. Найти заряд q капельки. Считать, что сила сопротивления пропорциональна скорости капельки.
Ответ: q = 4,1 10-17 Кл.
7. В плоский конденсатор параллельно пластинам на равном расстоянии от них влетает α частица с некоторой начальной скоростью v0. К пластинам конденсатора приложено напряжение U = 3000 В. Расстояние между пластинами d = 2 см, длина конденсатора l = 10 см. Какова должна быть предельная на-
чальная скорость v0 α частицы, чтобы она не вылетел из конденсатора?
Ответ: v0 = 3,64 107 м/с.
8. Элемент с ЭДС в ε = 1,1 В и внутренним сопротивлением в r = 1 Ом замкнуты на внешнее сопротивление R = 9 Ом. Найти ток I в цепи, напряжение UR во внешней цепи, напряжение Ur внутри элемента и КПД η элемента.
Ответ: I = 0,11 А; UR = 0,99 В; Ur = 0,11 В; η = 0,9.
9. |
В схеме, изображенной на рис. 1.8, ЭДС батареи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
R2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||
ε = 100 В, сопротивления R1 = R3 = 40 Ом и R4 = 34 Ом. Найти |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
R1 |
|
|
|
|
|
|
|
|
R3 |
|||
ток I |
|
через резистор R2 = 80 Ом и мощность P , выделяющую- |
|
|
|
R4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ся на нем. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Рис. 1.8 |
|
|
|
|||||||||
Ответ: I2 = 0,4 А; U2 = 32 В. |
|
|
|
|
|
|
|||||||||
10. Батарея с ЭДС ε = 240 В и внутренним сопротивлением r = 1 Ом замкнута на внешнее сопротивление R = 23 Ом. Найти полную мощность P0, полезную мощность Р и КПД η батареи.
Ответ: P0 = 2,4 кВт; P = 2,3 кВт; η = 96 %.
11. На рис. 1.9 изображено сечение двух прямолинейных бесконечно длин-
ных проводников с током. Расстояние AB |
I1 |
|
I2 |
|
|
между проводниками равно 10 см, I1 = 20 |
|
|
+ |
М3 |
|
А и I2 = 30 А. Найти напряженность маг- М1 |
А |
М2 |
B |
||
|
|||||
нитного поля Н, вызванного токами I1 и I2 |
|
Рис. 1.9 |
|
|
вточках М1, М2 и М3. Расстояния М1А = 2 см, АМ2 = 4 см, BМ3 = 3 см.
Ответ: H1=120 А/м; H2 = 159 А/м; H3 = 135 А/м.
12.Два прямолинейных длинных проводника расположены параллельно на расстоянии a = 5 см друг от друга. По проводникам текут токи I = 5 А в одном направлении. Найти величину и направление индукции магнитного поля В
вточке, находящейся на расстоянии l = 10 см от каждого проводника.
Ответ: В = 5 мкТл, направлено В вдоль прямой, соединяющей проводники.
13. В однородном магнитном поле с индукцией В = 0,5 Тл, движется равномерно проводник длиной l = 10 см. По проводнику течет ток I = 2 А. Скорость движения проводника v = 20 см/с и направлена перпендикулярно к направлению магнитного поля. Найти работу А перемещения проводника за время t = 10 с и мощность Р, затраченную на это перемещение.
Ответ: A = 0,2 Дж; P = 20 мВт.
16
14. Скорость самолета с реактивным двигателем v = 950 км/ч. Найти ЭДС индукции ε, возникающую на концах крыльев такого самолета, если вертикальная составляющая напряженности земного магнитного поля Нв = 39,8 А/м и размах крыльев самолета l = 12,5 м.
Ответ: ε = 165 мВ.
15. Круговой проволочный виток площадью S = 100 см2 находится в однородном магнитном поле, индукция которого B = 1 Тл. Плоскость витка перпендикулярна направлению магнитного поля. Определить среднее значение ЭДС индукции ε, возникающей в витке при выключении поля за время t = 0,01 с.
Ответ: ε = 1 В.
16. Катушка с активным сопротивлением R = 10 Ом и индуктивностью L включена в цепь переменного тока напряжением U = 127 В и частотой f = 50 Гц. Найти индуктивность L катушки, если известно, что катушка потребляет мощность Р = 400 Вт и сдвиг фаз между током и напряжением ϕ = 60°.
Ответ: L = 55 мГн.
1.4. Задачи для самостоятельной работы
1.Два одинаковых металлических заряженных шарика массой m = 0,2 кг каждый находятся на некотором расстоянии друг от друга. Найти заряд шариков q, если известно, что на этом расстоянии их электростатическая энергия в миллион раз больше их взаимной гравитационной энергии.
Ответ: q = 17 нКл.
2.Два точечных заряда q1 = 7 нКл и q2 = - 13 нКл расположены на рас-
стоянии a = 5 см. Найти напряженность электрического поля Е в точке, находящейся на расстояниях b = 3 см и c = 4 см от зарядов. Рассмотреть различные
варианты. Сделать чертеж. Ответ: Е = 105 В/м.
3.В вершинах правильного шестиугольника со стороной a = 3 см расположены три положительных и три отрицательных заряда. Найти напряженность электрического поля в центре шестиугольника для двух случаев расположения зарядов: а) заряды разного знака чередуются, б) заряды одного знака расположены группой из трех зарядов. Каждый заряд q = 1,5 нКл.
Ответ: а) Е = 0, б) Е = 60 кВ/м.
4.Найти плотность ρ материала шариков одинакового радиуса и массы, подвешенных на нитях так, что их поверхности соприкасаются, если известно, что при погружении этих шариков в керосин угол расхождения нитей стал ра-
вен 2α = 54°.
Ответ: ρ = 2,55 103 кг/м3.
5. В плоском горизонтально расположенном конденсаторе заряженная капелька ртути находится в равновесии при напряженности электрического поля E = 60 кВ/м. Заряд капли q = 8 10-19 Кл. Найти радиус капли R.
Ответ: R = 0,44 мкм.
17
6.До какого расстояния r могут сблизиться два электрона, если они дви-
жутся навстречу друг другу с относительной скоростью v0 = 106 м/с?
Ответ: r = 5,1 10-10 м.
7.Шарик массой m = 1 г и зарядом q = 10 нКл перемещается из точки A,
потенциал которой ϕ1 = 600 В, в точку B, потенциал которой ϕ2 = 0. Чему была равна его скорость v1 в точке A, если в точке B она стала равной v2 = 20 см/c.
Ответ: v1 = 16,7 см/с.
8.Между двумя вертикальными пластинами на одинаковом расстоянии от них падает пылинка. Вследствие сопротивления воздуха скорость падения пылинки постоянна и равна v = 2 см/с. Через какое время t после подачи на пластины напряжения U = 3 кВ пылинка достигает одной из пластин? Какое расстояние l по вертикали пылинка пролетит до попадания на пластину? Расстоя-
ние между пластинами d = 2 см, масса пылинки m = 2 10-9 г, заряд ее q = 6,5 10-17 Кл. Примечание: сила сопротивления при движении пылинки в воздухе пропорциональна ее скорости.
Ответ: t = 1 с, l = 2 см.
9. Протон и α-частица, двигаясь с одинаковой скоростью, влетают в плоский конденсатор параллельно пластинам. Во сколько раз отклонение протона полем конденсатора будет больше отклонения α-частицы?
Ответ: в 2 раза.
10.Элемент с ЭДС ε = 1,6 В имеет внутреннее сопротивление r = 0,5 Ом. Найти КПД η элемента при силе тока I = 2,4 А.
Ответ: η = 25 %.
11.Элемент с ЭДС ε = 2 В имеет внутреннее сопротивление r = 0,5 Ом. Найти напряжение на внутреннем Ur и внешнем U R участках цепи при токе в
цепи I = 0,25 А. Чему равно внешнее сопротивление R и какая на нем выделяется мощность P?
Ответ: R = 7,5 Ом; U R = 1,875 В; Ur = 0,125 В; Р = 0,47 Вт. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
12. Сопротивления резисторов в схеме на рис. 1.10 |
одинаковы и |
|
|
|
|
V |
|
|
|||
равны R = 200 Ом, сопротивление вольтметра RV = 1 |
кОм. Вольт- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
метр показывает напряжение U = 100 В. Найти ЭДС ε батареи. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
Рис. 1.10 |
|
||||||||||
Ответ: ε = 170 В. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
13. Найти внутреннее сопротивление r генератора, если известно, что мощность, выделяемая во внешней цепи, одинакова при двух значениях внешнего сопротивления R1 = 5 Ом и R2 = 0,2 Ом. Найти КПД η генератора в каждом из этих случаев.
Ответ: r = 1 Ом; η1 = 83,3 %; η2 = 16,7 %.
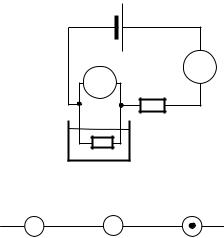
14. Калориметр К имеет спираль сопротивлением R1, которая включена, как показано на рис. 1.11. ЭДС батареи ε = 110 В, КПД спирали η = 80 %. В калориметр налит керосин массой m = 500 г. Амперметр показывает ток I = 2 А, а
|
18 |
|
|
|
вольтметр напряжение U = 10,8 В. Чему равно сопротивле- |
|
ε |
||
ние спирали? Найти удельную теплоемкость с керосина, ес- |
|
|||
|
|
|||
ли через время τ = 5 мин после пропускания тока через спи- |
V |
A |
||
раль керосин нагрелся на |
t = 5 °C. Сопротивлением бата- |
R2 |
||
реи и амперметра пренебречь. Сопротивление вольтметра |
R1 |
|
||
считать бесконечно большим. |
|
|
||
|
|
K |
||
Ответ: R1 = 5,4 Ом; с = |
2,1 кДж/(кг К). |
|
|
|
|
|
|
||
15. На рис. 1.12 изображено сечение трех пря- |
|
Рис. 1.11 |
||
молинейных бесконечно длинных проводников с |
I1 |
I2 |
I3 |
|
током. Расстояния AB = BC = 5 см, токи I1 = I2 = I и |
+ |
+ |
|
|
I3 = 2I. Найти точку на прямой AC, в которой ин- |
A |
B |
C |
|
дукция магнитного поля этих токов равна нулю. |
|
Рис. 1.12 |
||
Ответ: на расстоянии а = 3,3 см от точки А. |
|
|
|
|
16.Найти распределение индукции В магнитного поля вдоль оси соленоида длиной L = 3 см и диаметром D = 2 см. По соленоиду течет ток I = 2 А, ка-
тушка имеет N = 100 витков. Составить таблицу значений В для значений x в интервале 0 ≤ x ≤3 см через каждые 0,5 см и построить график.
17.Электрон, ускоренный разностью потенциалов U = 1000 В, влетает в однородное магнитное поле, перпендикулярное направлению его движения c
индукцией В = 1,19 10-3 Тл. Найти радиус кривизны R траектории электрона, период обращения T его по окружности, момент импульса L электрона.
Ответ: R = 9 см; T = 30 нс; L = 1,5 10-24 кг м2/с.
18.В однородном магнитном поле с индукцией В = 1 Тл движется равномерно проводник длиной l = 20 см со скоростью v = 20 см/с перпендикулярно направлению магнитного поля. По проводнику течет ток I = 1 А. Найти работу A при перемещении проводника за время t = 10 c.
Ответ: А = 0,2 Дж.
19.Горизонтальный стержень длиной l =1 м вращается вокруг вертикальной оси, проходящей через один из его концов. Ось вращения параллельна си-
ловым линиям магнитного поля c индукцией B = 5 10-5 Тл. При какой частоте
вращения n разность потенциалов на концах этого стержня U = 1 мВ? Ответ: n = 6,4 с-1.
20. В цепь переменного тока напряжением U = 220 В и частотой f = 50 Гц включены последовательно емкость С = 35,4 мкФ, резистор R = 100 Ом и индуктивность L = 0,7 Гн. Найти ток I в цепи и напряжения U R , UC и U L на от-
дельных элементах. Определить мощность Р и сдвиг фаз ϕ между током и напряжением.
Ответ: I = 1,34 А, U R = 134 В, UC = 121 В, U L = 295 В,P = 180 Вт, ϕ = 52°.

19
1.5. Задачи для контроля
1.Кольцо диаметром d = 10 см заряжено равномерно зарядом q = 5 нКл. Найти потенциал ϕ электрического поля на оси кольца как функцию расстояния x до его центра. Построить примерный график зависимости.
2.В плоском горизонтальном конденсаторе заряженная капелька ртути находится в равновесии при напряженности электрического поля E = 60 кВ/м. За-
ряд капли q = 8 нКл. Найти радиус капли. Плотность ртути ρ = 13,6 г/см3.
3. Пластины плоского конденсатора имеют заряды q1 = 2 нКл и q2 = – 4 нКл. Площадь пластин S = 100 см2. Найти напряженность электрического поля E внутри и снаружи конденсатора.
4. Элемент с ЭДС ε = 1,6 В имеет внутреннее сопротивление r = 0,6 Ом. Найти КПД η элемента при токе в цепи I = 2,4 А.
5. На рис. 1.13 приведена схема, для которой проведены измерения. По данным измерений I = 0,1 A и U = 6 B определить ЭДС батареи, мощность на резисторе и КПД батареи. Сопротивление резистора R = 100 Ом, внутреннее сопротивление батареи r = 0,1 Ом.
ε, r 

V R
A  Рис. 1.13
Рис. 1.13
6. Найти внутреннее сопротивление генератора, если известно, что мощность, выделяемая во внешней цепи, одинакова при двух значе-
ниях внешнего сопротивления 5 Ом и 0,2 Ом. Найти КПД генератора в каждом из этих случаев.
7. Два прямолинейных длинных проводника расположены параллельно на расстоянии a = 10 см друг от друга. По проводникам текут токи I = 5 А в противоположных направлениях. Найти величину и направление индукции магнитного поля В в точке, находящейся на расстоянии r = 10 см от каждого проводника.
8. На рис. 1.14 изображены сечения двух пря- |
I1 |
I2 |
молинейных бесконечно длинных проводников с |
|
|
M1 А M2 |
В M3 |
|
током. Расстояние между проводниками a = 10 см, |
Рис. 1.14 |
|
токи I1 = 20 А, I2 = 30 А. Найти напряженности |
|
магнитного поля в точках М1, М2 и М3. Расстояния АМ1 = 2 см, АМ2 = 4 см, ВМ3 = 3 см.
9.В магнитном поле с индукцией B = 0,05 Тл вращается стержень длиной l = 1 м с угловой скоростью ω = 20 рад/с. Ось вращения проходит через конец стержня и параллельна магнитному полю. Найти ЭДС ε на концах стержня.
10.Электрон, ускоренный разностью потенциалов U = 1000 В, влетает в однородное магнитное поле, перпендикулярное направлению его движения. Индукция магнитного поля B = 1,19 мТл. Найти радиус кривизны R траектории электрона.
