
ЭлектрикаОптикаЗадачи2013
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ КАФЕДРА ОБЩЕЙ ФИЗИКИ И ДИДАКТИКИ ФИЗИКИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ для проведения практических занятий
по физике для студентов биологического факультета (электричество и оптика)
Донецк 2013
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ КАФЕДРА ОБЩЕЙ ФИЗИКИ И ДИДАКТИКИ ФИЗИКИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ для проведения практических занятий по физике
для студентов биологического факультета (электричество и оптика)
Рекомендовано к изданию решением Ученого совета физическо-технического факультета ДонНУ
(протокол № 10 от 25.06.13)
Донецк 2013
УДК 378. 147:52
Методические указания для проведения практических занятий по физике для студентов биологического факультета (электричество и оптика) / Б.И. Бешевли, О.Б. Демина, А.Н. Семко / Под ред. А.Н. Семко – Донецк:
ДонНУ, 2013. – 46 с.
В методических указаниях приведены задачи по электричеству и оптике в рамках рабочей программы курса физики для студентов биологического факультета университета. В соответствии с программой курса тематика и количество задач рассчитаны для аудиторной и самостоятельной работы и для контроля знаний и умений. По каждой теме дана сводка основных формул и приведены примеры решения типовых задач с подробным объяснением. Рассмотрена организация самостоятельной работы студентов. Приведены графики проведения практических и лабораторных занятий, модульного контроля, программа курса общей физики по электричеству и оптике и список вопросов для контроля. Представлены образцы контрольных работ, тестов и экзаменационных билетов по электричеству и оптике.
Предназначены для студентов биологического факультета университета.
Ответственный за выпуск: доцент, к.ф.-м.н., А. Е. Зюбанов
Составители:
Б.И. Бешевли, О.Б. Демина, А.Н. Семко
Рецензент: д.ф.-м.н., профессор В. М. Юрченко
3
СОДЕРЖАНИЕ
1. |
Электричество..................................................................................... |
4 |
|
1.1. Сводка основных формул.............................................................. |
4 |
|
1.2. Примеры решения типовых задач................................................. |
9 |
|
1.3. Задачи для работы в аудитории.................................................. |
14 |
|
1.4. Задачи для самостоятельной работы......................................... |
16 |
|
1.5. Задачи для контроля.................................................................... |
19 |
2. |
Оптика................................................................................................. |
20 |
|
2.1. Сводка основных формул............................................................ |
20 |
|
2.2. Примеры решения типовых задач............................................... |
24 |
|
2.3. Задачи для работы в аудитории.................................................. |
29 |
|
2.4. Задачи для самостоятельной работы......................................... |
31 |
|
2.5. Задачи для контроля.................................................................... |
33 |
3. |
Организация самостоятельной работы........................................ |
35 |
|
3.1. Программа курса........................................................................... |
35 |
|
3.2. График лабораторных и практических занятий.......................... |
37 |
|
3.3. Вопросы для контроля.................................................................. |
39 |
|
3.4. Критерии оценивания знаний....................................................... |
41 |
|
3.5. Образцы типовых заданий для контроля.................................... |
43 |

4
1. ЭЛЕКТРИЧЕСТВО
1.1. Сводка основных формул
Электрическое поле в вакууме
В природе существует два вида зарядов: положительные и отрицательные. По закону Кулона точечные заряды q1 и q2, взаимодействуют с силой
F = q1q2 , 4πε0r2
где r - расстояние между зарядами, ε0 = 8,85 10-12 Ф/м – электрическая постоянная. Сила направлена вдоль прямой, соединяющей заряды. Одноименные заряды отталкиваются, а разноименные – притягиваются.
Напряженность электрического поля E равна отношению силы, действующей на заряд, к величине заряда
EG = Fq .
Напряженность поля точечного заряда определяется выражением
EG = 4πεq 0 rr3 .
По принципу суперпозиции напряженности полей складываются
EG = ∑n EGi .
i=1
По теореме Остроградского – Гаусса поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на ε0
G |
G |
= |
1 |
n |
q |
. |
∫EdS |
|
∑qi = |
ε0 |
|||
S |
|
|
ε0 i=1 |
|
||
Напряженность поля бесконечной равномерно заряженной плоскости с по-
верхностной плотностью σ равна
E = σ . 2ε0
Потенциал поля точечного заряда равен
ϕ= 4πεq 0r
Для потенциала поля системы зарядов справедлив принцип суперпозиции
n |
n |
qi |
|
|
ϕ= ∑ϕi = ∑ |
|
. |
||
4πε |
r |
|||
i=1 |
i=1 |
|
0 i |
|
Проекция вектора напряженности E на произвольную прямую х в пространстве связана с потенциалом выражением

5
Ex = −ddxϕ .
Работа сил электрического поля по перемещению заряда q из точки с по-
тенциалом ϕ1 в точку с потенциалом ϕ2 равна
A = q(ϕ1 − ϕ2 ).
Электрическое поле в веществе
ЭлектрическоеG поле в диэлектриках характеризуют электрическим смещением D , которое определяется соотношением
D = εε0 E ,
где ε - относительная диэлектрическая проницаемость вещества. Теорема Остроградского-Гаусса для вектора D имеет вид
∫DdS = ∫ρdV .
S V
где ρ = dq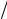 dV - объемная плотность заряда.
dV - объемная плотность заряда.
Для однородного и изотропного диэлектрика сила Кулона, напряженность и потенциал поля точечного заряда в ε раз меньше чем в вакууме
F = |
q1q2 |
, |
|
|
− |
qr |
, ϕ = |
q |
. |
|
E |
||||||||||
4πεε0r2 |
|
4πεε0 r 3 |
4πεε0 r |
|||||||
|
|
|
|
|
|
|
Проводники имеют свойство накапливать заряд. Емкость C уединенного проводника определяется отношением его заряда q к потенциалу ϕ
C = ϕq .
Емкость конденсатора равна отношению его заряда q к напряжению U между обкладками
C = ϕ1 −q ϕ2 = Uq .
Емкость плоского конденсатора равна
C = εεd0 S ,
где S – площадь пластин конденсатора, d - расстояние между пластинами. Заряженный конденсатор имеет энергию
W = CU 2 = qU = q 2 . 2 2 2C
Конденсаторы соединяют в батареи последовательно и параллельно. При последовательном соединении заряд конденсаторов одинаковый, напряжения складываются, емкость батареи определяется выражением
1 |
= ∑ |
1 |
, |
U = ∑Ui , q1 = q2 =... = qn . |
C |
|
|||
i Ci |
i |
|||
При параллельном соединении емкость батареи и заряды складываются, а напряжение на конденсаторах одинаковое

6
C = ∑Ci , |
q = ∑qi , |
U1 =U2 =... =Un . |
|||||
i |
|
i |
|
|
|
|
|
Электрическое поле обладает энергией. Плотность энергии w электриче- |
|||||||
ского поля (энергия единицы объема) определяется выражением |
|||||||
|
w = |
ED |
= |
εε |
0 |
E 2 |
. |
|
2 |
|
2 |
||||
|
|
|
|
|
|||
Постоянный ток
Сила тока равна отношению заряда dq, перенесенного через поперечное сечение проводника, ко времени dt, за которое перенесен заряд
I = dq . G dt
Плотность тока j определяется величиной заряда носителей тока, их кон-
центрацией n и средней скоростью упорядоченного движения uG j = qnuG.
Сила тока выражается через плотность тока интегрированием по поперечному сечению проводника
I = ∫ jdS .
S
По закону Ома сила тока I на участке цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R
I = UR .
Сопротивление цилиндрического проводника длиной l с площадью поперечного сечения S рассчитывается по формуле
R =ρSl ,
где ρ- удельное сопротивление материала проводника. G
В дифференциальной форме закона Ома плотность тока j пропорцио-
нальна напряженности электрического поля E j = E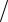 ρ
ρ
Количество теплоты dQ , выделяющееся в проводнике с сопротивлением R
при прохождении по нему тока I за малое время dt, по закону Джоуля-Ленца, равно
dQ = I 2 Rdt = IUdt .
Для замкнутой цепи по закону Ома сила тока пропорциональна ЭДС и обратно пропорциональна полному сопротивлению
I = R ε+ r ,
где ε - ЭДС источника тока, R и r – внешнее и внутреннее сопротивление цепи. При последовательном соединении проводников сила тока в проводниках
одинакова, а напряжения и сопротивления складываются

7
R = ∑Rk , U = ∑Uk , I1 = I2 =... = Ik .
При параллельном соединении проводников напряжение на проводниках одинаковое, а сила тока и величины, обратные сопротивлению, складываются
U1 =U2 =... =Uk , I = ΣIk , |
1 |
= Σ |
1 |
. |
R |
|
|||
|
|
Rk |
||
Для расчета разветвленных цепей используются два правила Кирхгофа. Первое правило: алгебраическая сумма токов в узле равна нулю
∑Ik = 0 .
k
Втекающие в узел токи - положительные, а вытекающие - отрицательные. Второе правило: для любого замкнутого контура алгебраическая сумма
произведений Ik Rk в ветвях равна алгебраической сумме ЭДС εk
∑Ik Rk = ∑εk . k k
Положительными считаются токи и ЭДС, направление которых совпадает с направлением обхода контура.
Магнитное поле
По закону Био–Савара–Лапласа элемент тока Idl создает магнитное поле с индукцией
dBG = μ0 I[dl ,rG] . 4π r3
Здесь r - радиус вектор, проведенный от элемента тока до точки наблюдения, μ0 = 4π 10-7 Гн/м – магнитная постоянная.
Для магнитного поля справедлив принцип суперпозиции
G |
G |
|
μ0 |
|
I[dli ,rGi ] |
|
||
B = ∑Bi = ∑ |
|
|
|
|
|
, |
||
4π |
r |
3 |
|
|||||
i |
i |
|
|
|
|
|
||
|
|
|
|
|
i |
|
|
|
где BGi - индукция магнитного поля отдельного проводника. |
||||||||
Индукция магнитного поля бесконечного прямого проводника равна |
||||||||
|
B = |
μ0 I |
, |
|
|
|
|
|
|
2πr |
|
|
|
|
|||
|
|
|
|
|
|
|
||
где r – расстояние до проводника. Линии индукции - концентрические окружности, их направление согласовано с током правилом правого винта.
Индукция магнитного поля в центре кругового тока радиуса R равна
B = μ20RI .
Циркуляция вектора магнитной индукции по любому замкнутому контуру L пропорциональна алгебраической сумме токов, охваченных контуром
∫L |
BG,dlG =μ0 |
∑Ii . |
|
|
n |
|
|
i=1 |
Ток считается положительным, если его направление согласовано с обходом контура по правилу правого винта.

8
На элемент тока Idl в магнитном поле с индукцией B действует сила Ам-
пера
dF = I[dl , B].
Направление силы определяется по правилу правого винта.
На контур с током в магнитном поле действует момент сил, равный
M =[ pGm , B], G
где pm = ISn - магнитный момента контура, S – его площадь, n - нормаль.
Магнитным потоком через поверхность S называется интеграл по поверхности
Φ = ∫BnGdS ,
где nG |
S |
- нормаль к поверхности. |
Электромагнитная индукция
При изменении магнитного потока, пронизывающего замкнутый контур, в нем возникает индукционный ток (явление электромагнитной индукции). По закону Фарадея ЭДС индукции в контуре равна скорости изменения магнитного потока
εin = −ddtΦ .
Знак «минус» соответствует правилу Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей.
Самоиндукция – возникновение ЭДС индукции при изменении тока в контуре. По закону Фарадея ЭДС самоиндукции определяется выражением
εci = −L dIdt ,
где L – индуктивность (коэффициент самоиндукции) контура.
Магнитное поле длинного соленоида однородное, сосредоточено внутри
соленоида, индукция магнитного поля направлена вдоль оси соленоида и равна
B =μμ0nI ,
где μ - относительная магнитная проницаемость вещества внутри соленоида, n = N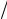 l - количество витков на единицу длины соленоида, N и l –количество
l - количество витков на единицу длины соленоида, N и l –количество
витков и длина соленоида.
Индуктивность и энергия длинного соленоида, объем которого V, равны
L =μμ0n2VI , |
W = |
LI |
2 |
. |
2 |
|
|||
|
|
|
|
Переменный ток
Переменным называется ток, изменяющийся со временем по гармоническому закону
U =U m cos ωt .
9
В цепи из последовательно соединённых конденсатора, катушки индуктивности и резистора сила тока изменяется по закону
I= I m cos(ωt − ϕ) ,
аамплитудные значения силы тока и напряжения связаны законом Ома
I m |
= |
U m |
|
, |
|
|
|
|
|
|
|||
|
R 2 + (X L − X C )2 |
|||||
X L = ωL , X C = |
1 |
, |
tg ϕ= |
X L − XC |
. |
|
|
|
|||||
|
|
ωC |
|
R |
||
Здесь XL и XC – индуктивное и ёмкостное сопротивления, ϕ - сдвиг фаз между током и напряжением, ω= 2πf - циклическая частота, f – частота.
Средняя мощность в цепи переменного тока зависит от сдвига фаз ϕ и определяется законом Джоуля – Ленца
P = IeUe cosϕ,
где Ie = Im  2 и Ue =Um
2 и Ue =Um  2 - действующие значения тока и напряжения.
2 - действующие значения тока и напряжения.
1.2. Примеры решения типовых задач
1. В центр квадрата, в вершинах которого находятся заряды q = 2,33 нКл, помещен отрицательный заряд q0 . Найти величину этого заряда, если резуль-
тирующая сила, действующая на каждый заряд, равна нулю. |
|
|
|
|
||||||
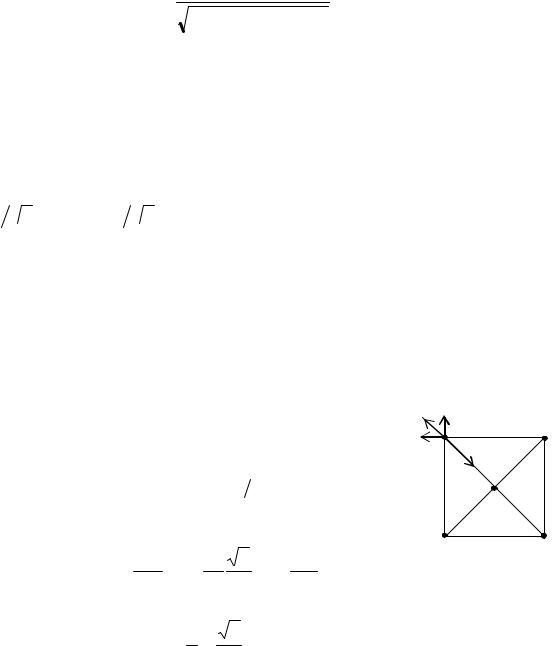
Решение. На рис. 1.1 приведено расположение зарядов и силы, действую- |
||||||||||
щие на заряд 1 со стороны остальных зарядов. По условию эти силы скомпен- |
||||||||||
сированы |
|
|
|
|
|
|
FG3 |
|
FG4 |
|
F2 + F3 + F4 + F0 = 0 . |
|
FG |
|
1 |
2q |
|||||
Спроектируем это равенство на прямую, совпадающую с |
q |
|||||||||
диагональю квадрата |
|
|
|
|
|
|
2 |
|
FG0 |
|
|
|
|
|
|
|
|
|
|
||
F3 + 2F4 cos(π 4)− F0 = |
0 . |
|
|
|
q |
|||||
Обозначив сторону квадрата a и используя закон Кулона, |
|
|
|
|||||||
|
|
|
|
|||||||
преобразуем это уравнение к виду |
|
|
|
|
qq0 |
|
|
q 4 |
3 q |
|
q2 |
q2 |
2 |
− k |
2 |
= 0 . |
|
|
|
Рис. 1.1 |
|
k 2a2 + 2k a2 2 |
|
a2 |
|
|
|
|
||||
Отсюда найдем искомый заряд |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
q0 |
|
|
+ |
|
|
=2,23 нКл. |
= q |
4 |
2 |
|
|||
|
|
|
|
|
2. Два шарика одинакового радиуса и массы m = 10 г подвешены на нитях так, что их поверхности соприкасаются, и погружены в керосин. После сооб-
щения шарикам заряда q0 = 2 10−6 Кл они оттолкнулись друг от друга и разо-
шлись на угол 2α = 45°. Найти плотность материала шариков, если расстояние от точки, подвеса до центра шарика l = 20 см. Плотность и относительная диэлектрическая проницаемость керосина ρk = 800 кг/м3, ε = 2.
