Лекции_ТУ

7.3.6 Апериодическое звено

Передаточная функция интегрирующего звена:

W (p) = 1 .

τ p + 1

Операторное уравнение системы:

(τ p + 1)X (p) = Y (p);

тогда дифференциальное уравнение системы (при нулевых начальных

условиях) имеет вид:

τ x′(t )+ x(t ) = y(t ).

Рассмотрим решение соответствующего однородного уравнения:

−1 t

τx′(t )+ x(t ) = 0 : xoo (t ) = c1e τ , c1 R.

Полученная функция не является периодической, что объясняет название звена.

ϕ (ω) = ArgW (iω) = arctg −τω = − arctgτω . 1

Запишем ЛАЧХ системы: L(ω ) = 20lgW (iω ) = −20lg 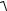1 + τ 2 ω 2 . График ЛАЧХ апериодического звена приведен на рис. 7.9 (пунктирная линия – график ЛАЧХ, сплошные линии – графики сопрягающих асимптот).

Рис. 7.9 – График ЛАЧХ апериодического звена

7.3.7 Колебательное звено

Передаточная функция интегрирующего звена:

Операторное уравнение системы:

(S 2 p 2 + 2ψ S p + 1)X (p) = Y (p);

тогда дифференциальное уравнение системы (при нулевых начальных условиях) имеет вид:

S 2 x′′(t )+ 2ψ S x′(t )+ x(t ) = y(t ).

Рассмотрим решение соответствующего однородного уравнения:

S 2 x′′(t ) + 2ψ S x′(t ) + x(t ) = 0 . Несложно показать, что корни характеристического

График ЛАЧХ колебательного звена приведен на рис. 7.10 (пунктирная линия – график ЛАЧХ, сплошные линии – графики сопрягающих асимптот).

Рис. 7.10 – График ЛАЧХ колебательного звена

Рассмотрим пример применения свойств и характеристик типовых звеньев.

Пример 7.2. Изобразить эскиз ЛАЧХ для системы с передаточной функцией:

Динамическая система содержит 5 типовых звеньев: 1) усилительное звено с параметром K = 3 ;

2) дифференцирующее звено первого порядка с параметром T1 = 1 ;

2

3) дифференцирующее звено первого порядка с параметром T2 = 1 ; 3

4) апериодическое звено с параметром τ1 = 1;

5) апериодическое звено с параметром τ 2 = 1 .

4

Изобразим отдельно графики ЛАЧХ каждого типового звена, составляющего систему (рис. 7.11–7.15).

Рис. 7.11 – График ЛАЧХ усилительного звена с параметром K = 3

Рис. 7.12 – График ЛАЧХ дифференцирующего звена первого порядка

с параметром T = 1 2

Рис. 7.13 – График ЛАЧХ дифференцирующего звена первого порядка

с параметром T = 1 3

Рис. 7.14 – График ЛАЧХ апериодического звена с параметром τ = 1

Рис. 7.15 – График ЛАЧХ апериодического звена с параметром τ = 1 4

Выпишем уравнения ЛАЧХ и их сопрягающих асимптот для каждого типового звена.

Вычислим значения ЛАЧХ системы в характерных точках.

Определим наклоны сопрягающих асимптот на различных участках:

ω(0;1): наклон 0 + 0 + 0 + 0 + 0 = 0 дБдек;

ω(1; 2): наклон 0 + 0 + 0 − 20 + 0 = −20 дБдек ;

ω(2; 3): наклон 0 + 20 + 0 − 20 + 0 = 0 дБдек;

ω(3; 4): наклон 0 + 20 + 20 − 20 + 0 = 20 дБдек;

ω(4; ∞): наклон 0 + 20 + 20 − 20 − 20 = 0 дБдек.

Для корректного расположения значений 2, 3, 4 на логарифмической оси частот требуется расчет значений: lg 2 ≈ 0,30, lg3 ≈ 0,48 , lg4 ≈ 0,60 .

Проведенные исследования позволяют построить эскиз ЛАЧХ системы как сумму графиков ЛАЧХ типовых звеньев, составляющих эту систему. Результирующий эскиз ЛАЧХ приведен на рис. 7.16.

Рис. 7.16 – Эскиз ЛАЧХ системы для примера 7.2

Контрольные вопросы к теме 7

Основной уровень

1.Что называется типовым звеном системы?

2.Перечислите названия типовых звеньев динамических систем и их передаточные функции.

Продвинутый уровень

1.Сформулируйте свойства типовых звеньев системы.

2.Как определить, какие типовые звенья и с какими параметрами содержит динамическая система?

3.Для чего применяется информация о типовых звеньях, составляющих систему?

8. Устойчивость линейных динамических систем

Понятие устойчивости системы связано со способностью системы возвращаться в положение (состояние) равновесия после исчезновения внешних сил, которые вывели систему из этого положения. Рассмотрим понятие устойчивости и его интерпретацию с точки зрения устойчивости механических систем.

Понятие устойчивости наглядно иллюстрируется на рис. 8.1–8.3, где изображен шар, лежащий в некотором углублении (рис. 8.1), на выпуклой поверхности (рис. 8.2), на плоскости (рис. 8.3). Положение равновесия шара характеризуется точкой A0 . При отклонении шара в точку A1 он будет стре-

миться возвратиться к положению равновесия – в точку A2 .

Определение. Динамическая система называется устойчивой, если после исчезновения возмущений она возвращается в исходное положение равновесия

(рис. 8.1).

Рис. 8.1 – Иллюстрация понятия устойчивой системы

Определение. Динамическая система называется неустойчивой, если после исчезновения возмущений она не возвращается ни в какое положение равновесия (рис. 8.2).

Рис. 8.2 – Иллюстрация понятия неустойчивой системы

Определение. Динамическая система называется нейтральной, если после исчезновения возмущений она возвращается в положение равновесия, отличное от исходного (рис. 8.3).

Рис. 8.3 – Иллюстрация понятия нейтральной системы

Определение. Система называется устойчивой «в большом», если определены границы области устойчивости, т. е. определены границы начальных отклонений, при которых система возвращается в исходное положение равновесия (рис. 8.4).

Рис. 8.4 – Иллюстрация понятия устойчивость «в большом»

На рис. 8.4 состояние равновесия устойчиво лишь до тех пор, пока отклонение не вышло за некоторую границу, определяемую точкой B . Выйдя за эту границу, шар уже не вернется в точку A0 .

Определение. Система называется устойчивой «в малом», если констатируется только факт устойчивости, но границы области устойчивости не определены.

Определение. Система называется устойчивой «в целом», если она возвращается в исходное положение равновесия для любых начальных отклонений.

Для линейных стационарных динамических систем, функционирование которых во времени описывается с помощью обыкновенных дифференциальных уравнений, рассматривается понятие асимптотической устойчивости.

8.1 Понятие асимптотической устойчивости

Определение. Динамическая система называется асимптотически устой- чивой, если свободное движение системы (свободные колебания системы) после снятия возмущения с течением времени затухают.

Пусть функционирование системы описывается дифференциальным уравнением вида:

Факт снятия возмущения означает y(t ) ≡ 0 , тогда свободное движение системы является решением уравнения:

с учетом некоторых начальных условий.

Таким образом, фраза «свободное движение системы с течением времени

затухает» означает, что lim xсв (t ) = 0 , где xсв (t ) – решение дифференциального

t→∞

уравнения (8.2).

Пример 8.1. Исследовать на асимптотическую устойчивость по определению систему, которая описывается дифференциальным уравнением: dx + 4x(t ) = 5 y(t ),

Свободное движение системы с течением времени затухает, следовательно, система асимптотически устойчива.

Пример 8.2. Исследовать на асимптотическую устойчивость по определению систему, которая описывается дифференциальным уравнением:

Следовательно, система не является асимптотически устойчивой.

8.2 Признак асимптотической устойчивости

Рассмотрим линейную стационарную ДС, которая описывается дифференциальным уравнением (8.1). Свободное движение этой системы описывается решением уравнения (8.2). Исследуем поведение xсв (t ) и выведем признак асимптотической устойчивости.

70 8. Устойчивость линейных динамических систем

Характеристическое уравнение для дифференциального уравнения (8.2) имеет вид:

корня λk . Изучим поведение xk (t ) при t → ∞ в случаях, когда:

1)λk – простой действительный корень;

2)λk – кратный действительный корень;

3)λk – простой комплексный корень;

4)λk – кратный комплексный корень.

1. Пусть λk – простой действительный корень, тогда xk (t ) имеет вид: xk (t ) = Сk eλk t , Ck R .

2. Пусть λk – кратный действительный корень, тогда xk (t ) имеет вид:

3. Пусть λk – простой комплексный корень, тогда существует сопряжен-

ный комплексный корень λ j = λ*k , и сумма соответствующих функций xk (t ) + x j (t ) имеет вид: