
лекция 5
.pdf1 ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В КОМПЬЮТЕРЕ
1. Формальные языки в курсе информатики
Информацию, циркулирующую в компьютере, можно разделить на два вида: обрабатываемая информация (данные) и информация, управляющая работой компьютера (команды, программы, операторы).
Информацию, представленную в форме, пригодной для хранения, передачи и обработки компьютером принято называть данными. Для каждого типа данных различается внешнее и внутреннее представление данных. Внешнее представление ориентировано на человека, определяет вид данных на устройствах вывода: на экране, на распечатке. Внутреннее представление — это представление на носителях информации в компьютере, т.е. в памяти, в линиях передачи информации. Компьютер непосредственно оперирует с информацией во внутреннем представлении, а внешнее представление используется для связи с человеком.
В самом общем смысле можно сказать, что языком представления данных ЭВМ является язык двоичных кодов. Однако с точки зрения приведенных выше свойств, которыми должен обладать всякий язык: алфавита, синтаксиса, семантики, прагматики, нельзя говорить об одном общем языке двоичных кодов. Общим в нем является лишь двоичный алфавит: 0 и 1. Но для различных типов данных различаются правила синтаксиса и семантики языка внутреннего представления. Одна и та же последовательность двоичных цифр для разных типов данных имеет совсем разный смысл. Например, двоичный код «0100000100101011» на языке представления целых чисел обозначает десятичное число 16683, а на языке представления символьных данных обозначает два символа «А+». Таким образом, для разных типов данных используются разные языки внутреннего представления. Все они имеют двоичный алфавит, но различаются интерпретацией символьных последовательностей.
Внутренним языком представления действий над данными (языком управления работой компьютера) является командный язык процессора ЭВМ. К внешним языкам представления действий над данными относятся языки программирования высокого уровня, входные языки пакетов прикладных программ, командные языки операционных систем, языки манипулирования данными в СУБД и пр.
Следует иметь в виду, что любой язык программирования высокого уровня включает в себя как средства представления данных (раздел данных), так и средства представления действий над данными (раздел операторов). То же самое относится и к другим перечисленным выше типам компьютерных языков.
2. Языки представления чисел: системы счисления
Тема «Системы счисления» имеет прямое отношение к математической теории чисел. Однако в школьном курсе математики она, как правило, не изучается. Необходимость изучения этой темы в курсе информатики связана с тем фактом, что числа в памяти компьютера представлены в двоичной системе счисления, а для внешнего представления содержимого памяти, адресов памяти используют шестнадцатеричную или восьмеричную системы.
Система счисления — это определенный способ представления чисел и соответствующие ему правила действия над числами.
Системы счисления делятся на позиционные и непозиционные. В позиционных системах любое число записывается в виде последовательности цифр, количественное значение которых зависит от места (позиции), занимаемой каждой из них в числе. Примеры: десятичная, восьмеричная, двоичная система и т.д.
Пример непозиционной системы счисления - римская система.
Информация в вычислительной машине представляется в двоичном коде (0 и 1), (да, нет), (вкл., выкл.). 0 и 1 - это 1 бит информации или 1 двоичный разряд. 1 байт - это 8 бит (8 двоичных разрядов). В компьютере 1 байт является наименьшей единицей информации, что соответствует одному знаку в командной строке (цифре, букве, специальному символу или пробелу).
1 Кбит = 1024 бит = 210 бит =~ 1000 бит (1 килобит).
1 Мбит = 1048576 бит = 220 бит =~ 1 000 000 бит (1 мегабит).
1 Гбит = 230 бит =~ 109 бит = 1 000 000 000 (1 гигабит).
В компьютерах IBM PC используются следующие единицы измерения информации: 1 б (1 байт), 1 Кб (1 килобайт или часто просто 1 К), 1 Мб (1 мегабайт или часто просто 1 М), 1 Гб (1 гигабайт). Между ними существуют следующие соотношения:
1 Кб = 210 б = 1024 б =~ 1000 б.
1 Мб = 220 б = 1024 Кб = 1048576 б =~ 1 000 000 б.
1 Гб = 230 б = 1024 Мб =~ 109 б = 1 000 000 000 б.
Представление информации, хранящейся в компьютерной памяти в ее истинном двоичном виде весьма громоздко из-за большого количества цифр. Имеется в виду запись такой информации на бумаге или вывод ее на экран. Для этих целей принято использовать восьмеричную или шестнадцатеричную системы счисления. В современных ПК чаще всего используется шестнадцатеричная система.
Существует простая связь между двоичным и шестнадцатеричным представлением числа. При переводе числа из одной системы в другую, одной шестнадцатеричной цифре соответствует 4-разрядный двоичный код. Это соответствие отражено в двоично-шестнадцатеричной таблице:
Двоично-шестнадцатеричная таблица
16 |
2 |
16 |
2 |
0 |
0000 |
8 |
1000 |
1 |
0001 |
9 |
1001 |
2 |
0010 |
А |
1010 |
3 |
0011 |
В |
1011 |
4 |
0100 |
С |
1100 |
5 |
0101 |
D |
1101 |
6 |
0110 |
Е |
1110 |
7 |
0111 |
F |
1111 |
Такая связь основана на том, что 16 = 24, и число различных 4-разрядных комбинаций из цифр 0 и 1 равно 16: от 0000 до 1111. Поэтому перевод чисел из «16» в «2» и обратно производится путем формальной перекодировки. Принято считать, что если дано шестнадцатеричное представление внутренней информации, то это равносильно наличию двоичного представления. Преимущество шестнадцатеричного представления состоит в том, что оно в 4 раза короче двоичного.
3. Язык логики и его место в базовом курсе
Логика — наука, изучающая методы установления истинности или ложности одних высказываний на основе истинности или ложности других высказываний. Основы логики как науки были заложены в IV в. до н.э. древнегреческим ученым Аристотелем. Правила вывода истинности высказываний, описанные Аристотелем (силлогизмы) оставались основным инструментом логики вплоть до второй половины XIX в., когда в трудах Дж. Буля, О. де Моргана и др. возникла математическая логика. Средствами этой новой науки все прежние достижения логики были переведены на точный язык математики. Развивается аппарат алгебры логики (булевой алгебры), исчисления высказываний, исчисления предикатов. Логика относится к числу дисциплин, образующих математический фундамент информатики. Знакомство учащихся с элементами математической логики в рамках кypca информатики может происходить в следующих аспектах:
•процедурно-алгоритмическом;
•в логическом программировании;
•схемотехническом.
К первому аспекту относится использование логических величин и логических выражений в языках программирования процедурного типа, а также в работе с электронными таблицами, с базами данных.
Под схемотехническим аспектом понимается знакомство с логическими схемами элементов компьютера: вентилей, сумматоров, триггера, предназначенных для обработки и хранения двоичной информации. При изучении данной темы следует обратить внимание учеников на то обстоятельство, что основой внутреннего языка компьютера является язык логики, булева алгебра. Это связано с двумя обстоятельствами: во-первых, внутренний язык компьютера и язык логики используют двоичный алфавит (0 и 1); во-вторых, все команды языка процессора реализуются через три логические операции: И, ИЛИ, НЕ.
Основные понятия математической логики
Высказывание (суждение) — это повествовательное предложение, в котором что-либо утверждается или отрицается. По поводу любого высказывания можно сказать, истинно оно или ложно. Например: «Лед — твердое состояние воды» — истинное высказывание.
Логические величины: понятия, выражаемые словами: ИСТИНА, ЛОЖЬ (true, false). Следовательно, истинность высказываний выражается через логические величины.
Логическая константа: ИСТИНА или ЛОЖЬ.
Логическая переменная: символически обозначенная логическая величина. Следовательно, если известно, что А, В, X, У и пр. — переменные логические величины, то это значит, что они могут принимать значения только ИСТИНА или ЛОЖЬ.
Логическое выражение — простое или сложное высказывание. Сложное высказывание строится из простых с помощью логических операций (связок).
Логические операции. В математической логике определены пять основных логических операций: конъюнкция, дизъюнкция, отрицание,
импликация, эквивалентность. Первые три из них составляют полную систему операций, вследствие чего остальные операции могут быть выражены через них (нормализованы). В информатике обычно используются эти три операции.
Конъюнкция (логическое умножение). В русском языке она выражается союзом И. В математической логике используются знаки & или Ù. Конъюнкция
— двухместная операция; записывается в виде: А Ù В. Значение такого выражения будет ЛОЖЬ, если значение хотя бы одного из операндов ложно.
Дизъюнкция (логическое сложение). В русском языке этой связке соответствуют союз ИЛИ. В математической логике она обозначается знаком
Ú. Дизъюнкция — двухместная операция; записывается в виде: A Ú В. Значение такого выражения будет ИСТИНА, если значение хотя бы одного из операндов истинно.
Отрицание
—
.
Логическая формула (логическое выражение) — формула, содержащая лишь логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА или ЛОЖЬ.
Правила выполнения логических операций отражены в следующей таблице, которая называется таблицей истинности
|
А |
В |
Ø |
А&В |
AÚ В |
|
|
|
|
|
|
1 |
и |
и |
л |
и |
и |
|
|
|
|
|
|
2 |
и |
л |
л |
л |
и |
|
|
|
|
|
|
3 |
л |
и |
и |
л |
и |
|
|
|
|
|
|
4 |
л |
л |
и |
л |
л |
|
|
|
|
|
|
Последовательность выполнения операций в логических формулах определяется старшинством операций. В порядке убывания старшинства логические операции расположены так: отрицание, конъюнкция, дизъюнкция. Кроме того, на порядок операции влияют скобки, которые можно использовать в логических формулах. Например: (А и Б) или (не А и В) или (не А и не Б)
4. Представление числовой информации в компьютере
Числа в памяти ЭВМ хранятся в двух форматах: в формате с фиксированной точкой и в формате с плавающей точкой. Под точкой здесь и в дальнейшем подразумевается знак разделения целой и дробной части числа. Формат с фиксированной точкой используется для хранения в памяти целых чисел.
1. Рассмотрим перевод целого десятичного числа в двоичную систему счисления.
Пусть Ац = а n-1 х 2 n-1 +... + а 1 х 2 1 + а 0 х 2 0
-поделим Ац на 2, тогда неполное частное будет а n-1 х 2 n-1 + … +а1 ,а остаток а0
-полученное неполное частное опять разделим на 2, остаток от деления будет а1 и т.д.
-на n-м шаге получим набор остатков а 0, а 1, а 2, ..., а n-1, которые входят в
двоичное представление числа Ац и совпадают с остатками от
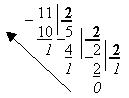
последовательного деления данного числа на 2. Но мы получим их в обратном порядке. Нужно только переписать их .
Ац = а n-1 а n-2 ... а 1 а 0
Пример 1. Перевести число 11 из десятичной системы счисления в двоичную систему.
Соберем остатки от деления в направлении, указанной стрелкой, начиная с последней единицы и получим число в двоичной системе счисления:
2. Задача перевода чисел из двоичной системы счисления в десятичную чаще всего возникает уже при обратном преобразовании вычисленных либо обработанных компьютером значений в более понятные пользователю десятичные цифры.
Пример 2: требуется перевести двоичное число 10110110 в десятичное. В этом числе 8 цифр и 8 разрядов (разряды считаются, начиная с нулевого, которому соответствует младший бит). В соответствии с уже известным нам правилом представим его в виде суммы степеней с основанием 2:
101101102 = (1·27)+(0·26)+(1·25)+(1·24)+(0·23)+(1·22)+(1·21)+(0·20) = 128+32+16+4+2 = 18210
3.Для записи внутреннего представления целого отрицательного числа (-
N)нужно: получить внутреннее представление положительного числа N; получить обратный код этого числа заменой 0 на 1 и 1 на 0; к полученному числу прибавить 1.
Пример 3: Определим по этим правилам внутреннее представление числа
160710.
1)0000 0110 0100 0111
2)1111 1001 1011 1000
3)_______________ +1
1111 1001 1011 1001 - результат
Описанный способ представления целого отрицательного числа называют дополнительным кодом. Старший разряд в представлении любого отрицательного числа равен 1. Следовательно, он указывает на знак числа и поэтому называется знаковым разрядом.
4. В разных типах ЭВМ используются разные варианты организации формата с плавающей точкой. Формат с плавающей точкой используется как для представления целочисленных значений, так и значений с дробной частью.

В математике такие числа называют действительными, в программировании — вещественными.
Формат с плавающей точкой предполагает представление вещественного числа R в форме произведения мантиссы (т) на основание системы счисления (л) в некоторой целой степени, которую называют порядком (р):
Порядок указывает, на какое количество позиций и в каком направлении должна сместиться («переплыть») точка в мантиссе. Например, 25,32410 = 0,25324´102. Чтобы не было неоднозначности, в ЭВМ используют нормализованную форму с плавающей точкой. Мантисса в нормализованной форме должна удовлетворять условию:
Для рассмотренного числа нормализованной формой будет: 0,25324 хЮ2.
В памяти ЭВМ мантисса представляется как целое число, содержащее только ее значащие цифры (нуль целых и запятая не хранятся). Следовательно, задача внутреннего представления вещественного числа сводится к представлению пары целых чисел: мантиссы (т) и порядка (р). В рассмотренном нами примере т = 25324, р = 2.
5. Представление символьной информации в компьютере. Кодовые таблицы
Начиная с конца 60-х годов компьютеры все больше стали использоваться для обработки текстовой информации, и в настоящее время большая часть персональных компьютеров в мире значительную часть времени занято обработкой именно ТЕКСТОВОЙ информации.
Для представления текстовой информации обычно используется 256 различных символов (прописные и заглавные буквы русского и латинского алфавита, цифры, знаки, графические символы и т. д.). Следовательно, для двоичного кодирования 1 символа необходим 1 байт информации или 8 двоичных разрядов. Таким образом, каждому символу соответствует своя уникальная последовательность из восьми нулей и единиц.
Присвоение символу конкретного двоичного кода — это вопрос соглашения, которое фиксируется в кодовой таблице. К сожалению, существуют пять различных кодировок русских букв, поэтому тексты — созданные в одной кодировке, не будут правильно отображаться в другой.
Структура таблицы кодировки ASCII
|
|
Порядковый номер |
|
|
Код |
|
|
|
|
Символ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Символы с номерами от 0 |
|
|
||||||
|
|
|
|
|
|
|
|
до 31 |
|
принято |
|
называть |
|
|
||
|
|
|
|
|
|
|
|
управляющими. |
|
|
|
|
|
|||
|
|
0 - 31 |
|
|
00000000 - 00011111 |
|
|
Их функция – управление |
|
|
||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
процессом |
вывода |
текста |
на |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
экран или печать, подача |
|
|
||||||
|
|
|
|
|
|
|
|
звукового |
сигнала, |
разметка |
|
|
||||
|
|
|
|
|
|
|
|
текста и т.п. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Стандартная |
|
часть |
|
|
||||
|
|
|
|
|
|
|
|
таблицы (английский). Сюда |
|
|
||||||
|
|
|
|
|
|
|
|
входят строчные и прописные |
|
|
||||||
|
|
|
|
|
|
|
|
буквы |
латинского |
алфавита, |
|
|
||||
|
|
|
|
|
|
|
|
десятичные |
цифры, |
знаки |
|
|
||||
|
|
32 - 127 |
|
|
00100000 - 01111111 |
|
|
препинания, |
всевозможные |
|
|
|||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
скобки, коммерческие и другие |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
символы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Символ 32 - пробел, т.е. |
|
|
||||||
|
|
|
|
|
|
|
|
пустая |
позиция |
в |
тексте. |
|
|
|||
|
|
|
|
|
|
|
|
Все остальные отражаются |
|
|
||||||
|
|
|
|
|
|
|
|
определенными знаками. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Альтернативная |
часть |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
таблицы |
|
|
|
(русская). |
|
|
||
|
|
|
|
|
|
|
|
Вторая половина |
кодовой |
|
|
|||||
|
|
|
|
|
|
|
|
таблицы |
|
ASCII, |
называемая |
|
|
|||
|
|
|
|
|
|
|
|
кодовой страницей (128 кодов, |
|
|
||||||
|
|
|
|
|
|
|
|
начиная с 10000000 и кончая |
|
|
||||||
|
|
|
|
|
|
|
|
11111111), |
|
может |
иметь |
|
|
|||
|
|
|
|
|
|
|
|
различные |
варианты, |
каждый |
|
|
||||
|
|
128 - 255 |
|
|
10000000 - 11111111 |
|
|
вариант имеет свой номер. |
|
|
||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
Кодовая |
страница |
в |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
первую |
очередь используется |
|
|
|||||
|
|
|
|
|
|
|
|
для размещения национальных |
|
|
||||||
|
|
|
|
|
|
|
|
алфавитов, |
|
отличных |
от |
|
|
|||
|
|
|
|
|
|
|
|
латинского. |
В |
|
русских |
|
|
|||
|
|
|
|
|
|
|
|
национальных |
кодировках |
в |
|
|
||||
|
|
|
|
|
|
|
|
этой |
|
части |
|
таблицы |
|
|
||
|
|
|
|
|
|
|
|
размещаются |
|
|
символы |
|
|
|||
|
|
|
|
|
|
|
|
русского алфавита. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
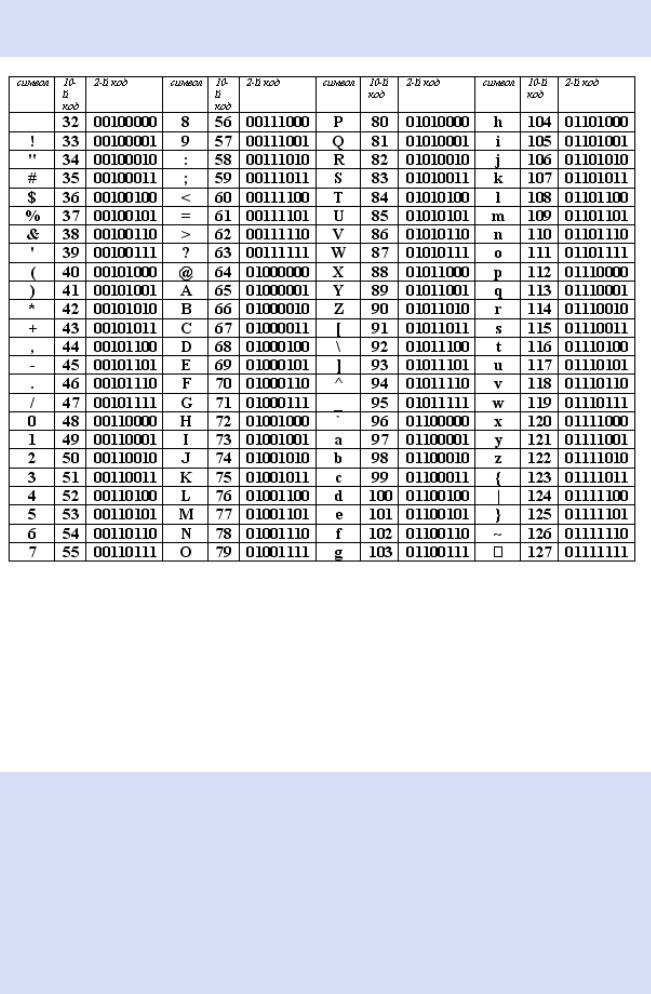
Первая половина таблицы кодов ASCII
Обращаю ваше внимание на то, что в таблице кодировки буквы (прописные и строчные) располагаются в алфавитном порядке, а цифры упорядочены по возрастанию значений. Такое соблюдение лексикографического порядка в расположении символов называется принципом последовательного кодирования алфавита.
Для букв русского алфавита также соблюдается принцип последовательного кодирования.
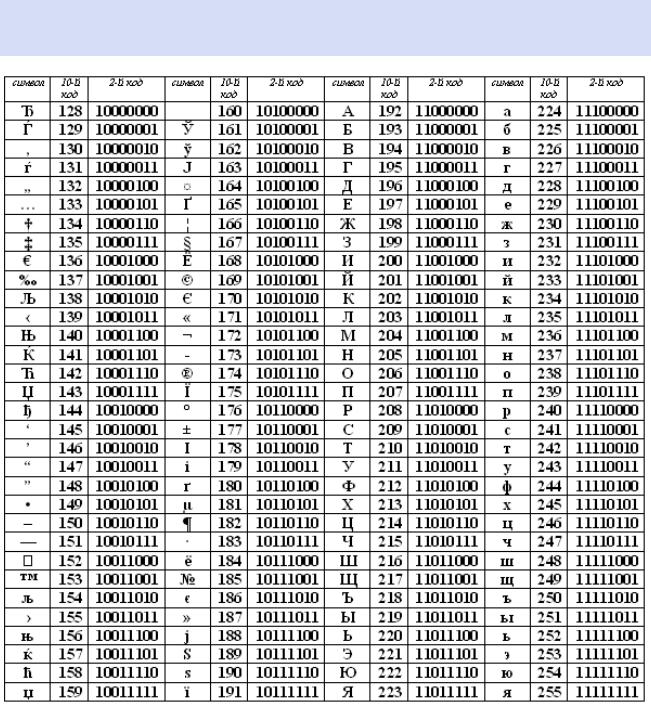
Вторая половина таблицы кодов ASCII
Хронологически одним из первых стандартов кодирования русских букв на компьютерах был КОИ8 («Код обмена информацией, 8-битный»). Эта кодировка применяется на компьютерах с операционной системой UNIX.
Наиболее распространенная кодировка — это стандартная кириллическая кодировка Microsoft Windows, обозначаемая сокращением СР1251 («СР» означает «Code Page», «кодовая страница»). Все Windows-приложения, работающие с русским языком, поддерживают эту кодировку. 28 = 256 символов
