
схеми геометрия 10 -11 класс
.doc
|
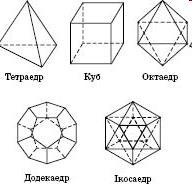
Типи правильних многогранників |
|||||
|
Назва |
Зображення |
Вид грані |
Число |
||
|
граней |
вершин |
ребер |
|||
|
Тетраедр
|
|
|
4 |
4 |
6 |
|
Гексаедр (куб)
|
|
|
6 |
8 |
12 |
|
Октаедр
|
|
|
8 |
6 |
12 |
|
Додекаедр
|
|
|
12 |
20 |
30 |
|
Ікосаедр |
|
|
20 |
12 |
30 |
|
Правильні многокутники |
||||||||||||||||||
|
Трикутник |
Співвідношення між |
Площа |
||||||||||||||||
|
а і R, а –сторона, R- радіус описаного кола |
R і r, r – радіус вписаного кола |
|||||||||||||||||
|
|
R = 2r |
S
=
|
||||||||||||||||
|
Квадрат |
|
R
= r |
S = a2 |
|||||||||||||||
|
Шестикутник |
a = R |
r
=
|
S
=
|
|||||||||||||||
|
Площа многокутників та круга |
||||||||||||||||||
|
Трикутник |
Довільний |
S
=
|
||||||||||||||||
|
Прямокутний |
S
=
|
|||||||||||||||||
|
Рівносторонній |
S
=
|
|||||||||||||||||
|
Паралелограм |
S
= ahа;
S =
|
|||||||||||||||||
|
Прямокутник |
S = ab |
|||||||||||||||||
|
Квадрат |
S = a2 |
|||||||||||||||||
|
Трапеція |
S
=
|
|||||||||||||||||
|
Коло |
S = πR2 |
|||||||||||||||||
|
Метричні співвідношення |
||||||||||||||||||
|
Прямокутний трикутник b=csinβ =atgβ = ccos = actg a= ccosβ = bctgβ= csin= btg
теорема
Піфагора:
a2
+b2=c2
A
Наслідки CB2=DBAB
C CD= ACCB: AB |
Трикутник
Теорема
синусів
Теорема
косинусів |
Паралелограм
А |
Теорема Птоломея
A |
|||||||||||||||
|
Призма |
|
|||||||||||||||||
|
Призмою називається многогранник, який складається з двох плоских многокутників, які лежать у різних площинах і суміщаються паралельним перенесенням, та всіх відрізків, що сполучають відповідні точки цих многокутників. Многокутники називаються основами призми, а відрізки, які сполучають відповідні вершини, - бічними ребрами призми. Висотою призми називається відстань між площинами її основ. Відрізок який сполучає дві вершини призми, що не належать одній грані, називається діагоналлю призми. |
|
|||||||||||||||||
|
Похила Якщо бічні ребра призми нахилені до основи під кутом - призма називається похилою і її бічні грані – паралелограми. |
Пряма Призма називається прямою, якщо її бічні ребра перпендикулярні до основ. Бічні грані прямої призми – прямокутники. |
|
||||||||||||||||
|
Т
перпендикулярний переріз
|
П’ятикутна Трикутна Чотирикутна
Пряма призма називається правильною , якщо її основи є правильними многокутниками |
|
||||||||||||||||
|
Я
А1 У паралелепіпеда всі грані паралелограми. Протилежні грані паралельні і рівні. Всі чотири діагоналі перетинаються в одній точці і точкою перетину діляться навпіл.
Т
А d12+ d22+ d32+ d42 = 4a2 +4b2+4c2 |
|
|||||||||||||||||
|
П Бічні ребра перпендикулярні до основ. Бічні грані - прямокутники, а основи – паралелограми.
|
П Бічні грані - прямокутники. Всі діагоналі рівні. d2 = a2 + b2 + c2 Sповн. = 2(ab+dc+ac) V = a b c |
К Всі грані - квадрати. Всі ребра рівні.
d
=
Sповн. = 6a2 V = a3 |
|
|||||||||||||||
|
Площа поверхні та об’єм призми |
|
|||||||||||||||||
|
Похила призма |
Пряма призма |
|
||||||||||||||||
|
Бічна поверхня |
Sосн. = Pпер. l, Росн. - периметр перпендикулярного перерізу; l – довжина бічного ребра. |
Sбіч. = Pосн. Н, Росн. - периметр основи; Н – висота. |
|
|||||||||||||||
|
Повна поверхня |
Sповн.= Sбіч. + 2Sосн. |
Sповн.= Sбіч. + 2Sосн. |
|
|||||||||||||||
|
Об’єм |
V = Sпер. l, l – бічне ребро |
V = Sосн. Н |
|
|||||||||||||||
|
Піраміда |
|
|||||||||||||||||
|
Пірамідою називається многогранник, який складається з плоского многокутника - основи піраміди і всіх відрізків, що сполучають вершину піраміди з вершинами основи, називаються бічними ребрами. Бічні грані – трикутники.
В
верхня основа
висота |
|
|||||||||||||||||
|
П Віссю правильної піраміди називається пряма (SO), яка містить її висоту. Бічні ребра рівні, бічні грані - рівні рівнобедрені трикутники. Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою (SF) й позначається l. |
Зрізаною пірамідою називається частина піраміди, яка міститься між її основою і перерізом піраміди, яке паралельне основі. Правильна зрізана піраміда: бічні грані - рівні рівнобічні
т
Б
нижня основа Апофеми рівні. |
|
||||||||||||||||
|
Площі поверхні і об’єм піраміди |
|
|||||||||||||||||
|
|
Піраміда |
Зрізана піраміда |
|
|||||||||||||||
|
Бічна поверхня |
Sбіч.= n – кількість сторін основи Правильна піраміда
Sбіч.= |
Sбіч.= n – кількість сторін основи Правильна зрізана піраміда
Sбіч.= р – периметр верхньої основи |
|
|||||||||||||||
|
Повна поверхня |
Sповн.= Sбіч. + Sосн. |
Sповн.= S + S +s, S- площа нижньої основи, s – площа верхньої основи |
|
|||||||||||||||
|
Об’єм |
V
=
|
V
=
|
|
|||||||||||||||
|
Тіла обертання |
||||||||||
|
Циліндр Круговим циліндром називається тіло, що складається з двох кругів, які не лежать в одній площині і суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів. Круги називаються основами циліндра, а відрізки, що сполучають точки кіл кругів, -твірними циліндра
У
|
Конус
одного з катетів
|
Зрізаний конус Зрізаним конусом називається частина конуса, яка лежить між основою і перерізом, паралельним основі конуса.
Утворений обертанням прямокутної трапеції навколо перпендикулярної до основ бічної сторони
|
Куля. Сфера. Кулею називається тіло, що складається з усіх точок простору, які знаходяться від даної точки на відстані, не більшій за дану. Ця точка називається центром кулі, а дана, відстань - радіусом кулі.
С
Утворена обертанням півкола наколо діаметра
|
|||||||
|
Частини кулі |
||||||||||
|
К
a2=h(2R-h) |
||||||||||
|
Площа поверхні та об’єм тіл обертання |
||||||||||
|
|
Циліндр |
Конус |
Зрізаний конус |
Куля. Сфера |
Кульовий сегмент |
Кульовий спектр |
||||
|
Бічна поверхня |
Sбіч. = 2RH |
Sбіч. = Rl |
Sбіч. = (R+r)l |
- |
Sбіч. = 2RH=(а2+Н2) |
- |
||||
|
Повна поверхня |
Sбіч. = 2R(R+H) |
Sбіч. = R(R+l) |
Sбіч. = (R+r)l +(R2+r2) |
S = 4R2 |
|
|
||||
|
Об’єм |
V = R2 H |
V
=
|
V
=
|
V
=
|
|
|
||||
|
Координати в просторі |
|
|||||||||
|
Н Ці координатні прямі називаються координатними осями: вісь х, вісь у, вісь z або вісь абсцис, вісь ординат, вісь аплікат відповідно, точку О називають початком координат. Кожна вісь точкою О розбивається на дві півосі — додатну, позначену стрілкою, і від'ємну. Площини, які проходять через х і у, х і z, у і z, називають координатними площинами і позначають відповідно: ху, хz, уz. Координатні площини розбивають весь простір на вісім частин, які називають октантами.
Відстань
між двома точками
А
(XA;
YA;
ZA)
i B (XB;
YB;
ZB)
обчислюється за формулою:
Координати середини відрізка точки С (Xс; Yс; Zс) - середини відрізка АВ:
|
|
|||||||||
Перетворення симетрії в просторі
|
Симетрія відносно |
А (x; y; z) |
1) точці А відносно точки О; 2) точці L відносно осі z; 3) точці N відносно площини ху; 4) точці К відносно площини уz; 5) точці М відносно точки О; 6) точці О відносно точки К. |
|
|
|
Точки О |
А1 (-x; -y; -z) |
|
||
|
Осі х |
А2 (x; -y; -z) |
|
||
|
Осі у |
А3 (-x; y; -z) |
|
||
|
Осі z |
А4 (-x; -y; z) |
|
||
|
Площини ху |
А5 (x; y; -z) |
|
||
|
Площини xz |
А6 (x; -y; z) |
|
||
|
Площини yz |
А7 (-x; y; z) |
|
||
|
Паралельним перенесенням у просторі називається таке перетворення, при якому довільна точка (х; у; z) фігури переходить у точку (х+ а; у + b; z + с), де числа а, b, с — одні і ті самі для всіх точок.
Паралельне
перенесення в просторі задають
формулами:
що виражають координати х1, у1, z1 точки, в яку переходить точка (х; у; z) при паралельному перенесенні.
|
|
|||
|
Вектори в просторі |
||||
|
Означення |
Вектором
називається
величини, які характеризуються
невід'ємним числом при даній одиниці
вимірювання (модулем) та напрямом,
(
Координатами
вектора
з
початком у точці А (XА,YA,
ZA)
і
кінцем у точці В (XB,
YB,
ZВ)
називають
числа
Рівність
векторів:
Нульовим
вектором
називається
вектор, кінець якого співпадає з
початком.(позначають
Довжина відрізка називається модулем (абсолютною величиною) вектора.
Вектор називається одиничним, якщо його абсолютна величина дорівнює одиниці. Одиничні вектори, які мають направлення додатних координатних півосей, називаються ортами. Орти прийнято називати е1(1; 0; 0); е12 (0; 1; 0); е3(0; 0; 1).
Для
вектора у просторі є місце
розкладання
,тобто кожен вектор можна представити
у вигляді:
|
|||
|
Дії над векторами |
Сума векторів
Різниця векторів
Добуток вектора на число
λ·
Скалярний
добуток векторів
Кут
між векторами
|
|||





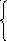

 D2=
ADDB;
D2=
ADDB;
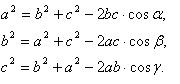


 Е2
+ ВС2
= 2(АВ2
+ ВЕ2)
Е2
+ ВС2
= 2(АВ2
+ ВЕ2)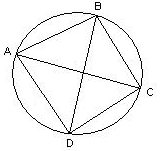 CBD=ABCD+BCAD
CBD=ABCD+BCAD
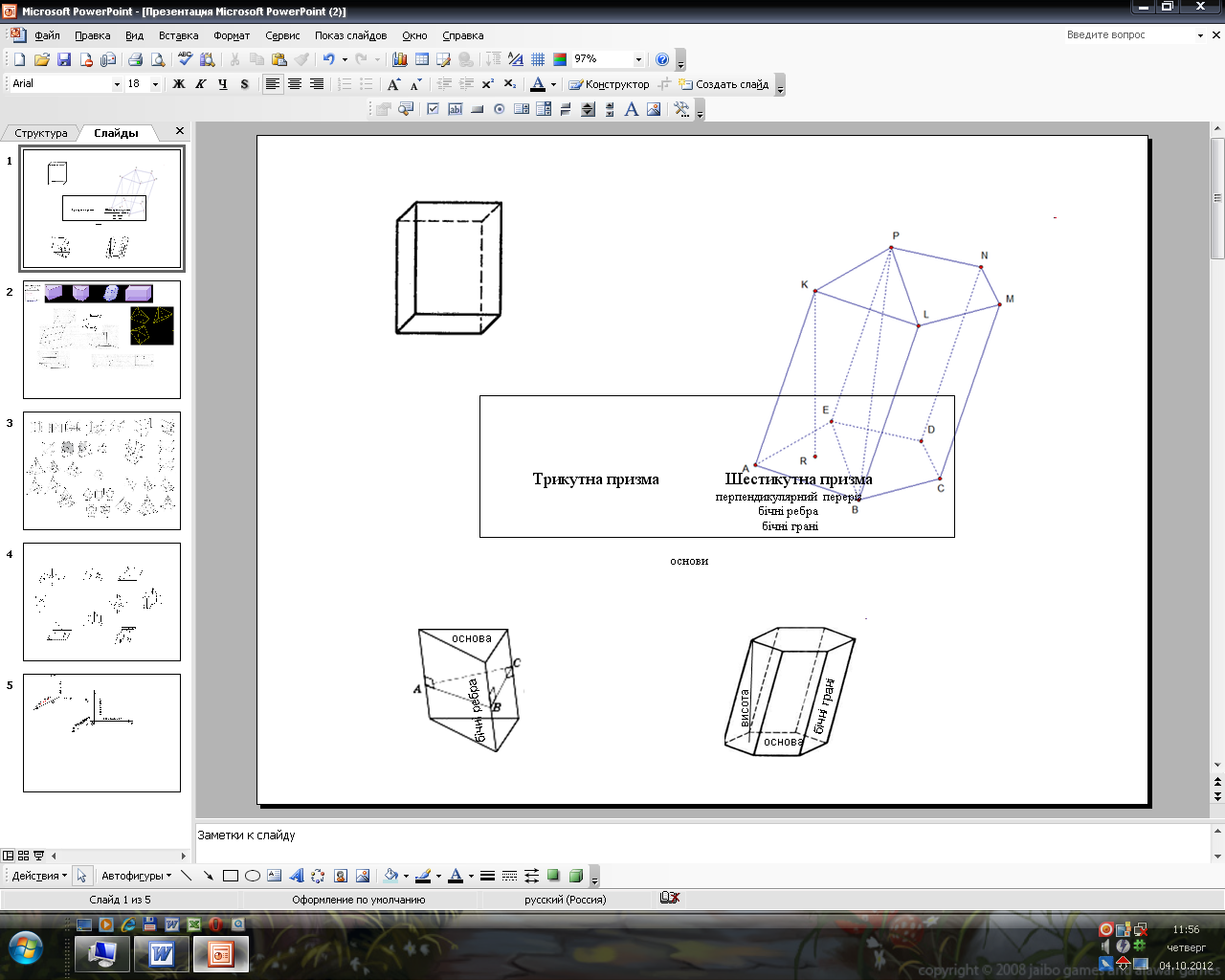
 рикутна
призма Шестикутна
призма
рикутна
призма Шестикутна
призма


 рямий
паралелепіпед:
рямий
паралелепіпед: рямокутний
паралелепіпед:
рямокутний
паралелепіпед:
 уб:
уб:
 исотою
піраміди називається
перпендикуляр, опущений з вершини
піраміди на площину о
исотою
піраміди називається
перпендикуляр, опущений з вершини
піраміди на площину о
 снови.
снови.
 іраміда
називається правильною,
якщо її основою є правильний многокутник,
а основа висоти збігається з центром
цього многокутника.
іраміда
називається правильною,
якщо її основою є правильний многокутник,
а основа висоти збігається з центром
цього многокутника.
 рапеції.
рапеції.
 ічні
ребра рівні.
ічні
ребра рівні.

 творений
обертанням прямокутника навколо
однієї з своїх сторін
творений
обертанням прямокутника навколо
однієї з своїх сторін Круговим
конусом
називається
тіло, яке складається з круга
-
основи конуса,
точки,
яка не
лежить у площині цього
круга
-
вершини конуса і всіх відрізків,
що сполучають вершини
конуса
з
точками основи.
Відрізки, що сполучають вершину
конуса
з точками кола основи, називаються
твірними
конуса
(l).
Круговим
конусом
називається
тіло, яке складається з круга
-
основи конуса,
точки,
яка не
лежить у площині цього
круга
-
вершини конуса і всіх відрізків,
що сполучають вершини
конуса
з
точками основи.
Відрізки, що сполучають вершину
конуса
з точками кола основи, називаються
твірними
конуса
(l). Утворений
обертанням прямокутного трикутника
навколо
Утворений
обертанням прямокутного трикутника
навколо

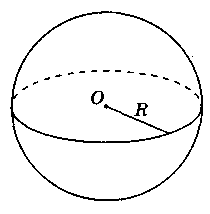 фера
є поверхнею
кулі.
фера
є поверхнею
кулі.

 ульовий
сектр Кульовий сегмент
ульовий
сектр Кульовий сегмент
 ехай
х,
у, z —
три попарно перпендикулярні координатні
прямі, які перетинаються в точці
О.
ехай
х,
у, z —
три попарно перпендикулярні координатні
прямі, які перетинаються в точці
О.
 Запишіть
координати точки, яка симетрична:
Запишіть
координати точки, яка симетрична:

