схеми геометрия 10 -11 класс
.doc|
Основні поняття і аксіоми стереометрії та найпростіші наслідки з них |
|||||||||
|
Стереометрія – це розділ геометрії, в якому вивчаються властивості просторових фігур. Основними фігурами в просторі є точка (А, В, С,…), пряма (a, b, c,…) і площина (, β, ,…). |
|||||||||
|
Способи задання точки в просторі |
Способи задання прямої в просторі |
||||||||
|
Двома прямими, які перетинаються |
|
b c Трьома попарно перетинаючимися площинами, якщо прямі перетину площин перетинаються |
Двома точками
|
Двома площинами, які перетинаються |
|||||
|
Способи задання площини в просторі |
|||||||||
|
Трьома точками, які не лежать на одній прямій |
Двома прямими, які перетинаються |
b
Двома паралельними прямими |
П
|
||||||
|
Група аксіом, які виражають основні властивості площин у просторі |
|||||||||
|
С1 |
С2 |
С3 |
|||||||
|
Яка б не була площина, існують точки, які належать цій площині, і точки, які не належать їй.
, |
Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку.
я а, |
Якщо дві різні прямі мають спільну точку, то через них можна провести площину, і до того ж тільки одну.
а,b β |
|||||||
|
Взаємне розміщення двох прямих у просторі |
|||||
|
Прямі а і b |
|
|
|||
|
|
|
|
|
|
|
|
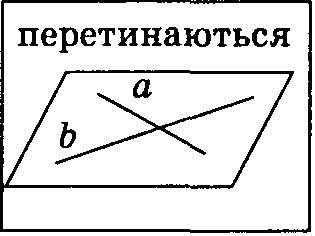
лежать в одній площині |
не лежать в одній площині |
|
|||
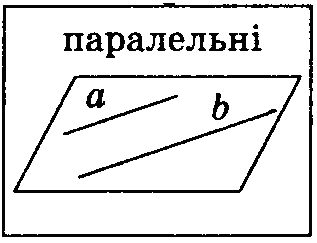
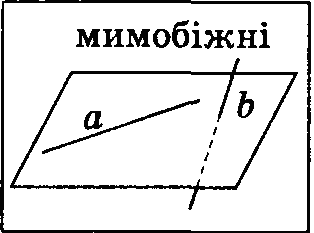
Прямі,
які не перетинаються і не лежать в
одній
площині, називаються мимобіжними.
Ознака мимобіжності прямих
Якщо одна з двох
прямих
лежить у площині,
а друга
перетинає цю
площину в точці,
яка
не лежить на першій прямій, то ці прямі
мимобіжні.





b
a
ab
a![]() b
b![]() b
b
|
|
Теореми існування площини |
Взаємне розміщення прямої ї площини |
|
|
|---|---|---|---|---|
|
|
1) яка проходить через дану пряму і дану точку Через пряму і точку, яка не належить їй, можна провести площину, і до того ж тільки одну.
2
А Через три точки, які не лежать на одній прямій, можна провести площину, і до того ж тільки одну.
|
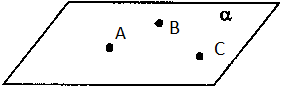
Теорема про належність площині прямої, дві точки якої належать площині Якщо дві точки прямої належать площині, то вся пряма належить цій площині.
Н
А |
|
|
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
Паралельність прямих і площин у просторі |
||||
|
Паралельні прямі |
Паралельні прямі і площини |
Паралельні площини |
||
|
Дві прямі в просторі називаються паралельними, якщо вони лежать в одній площині і не перетинаються. ОЗНАКА:
Теорема
Дві прямі, паралельні третій, паралельні
між собою.
(c||a, a||b) c || b Теорема про існування і єдність прямої, яка проходить через дану точку і паралельна даній прямій
Ч Ab, Aa, a||b |
Пряма і площина називаються паралельними, якщо вони не перетинаються. ОЗНАКА:
Я
(b,
b||a,
a
)
b||
ВЛАСТИВІСТЬ: Будь-яка площина, яка проходить через пряму паралельну даній площині або |
ОЗНАКИ:
1 2. Якщо кожна з двох даних площин паралельна третій площині, то дані дві площини паралельні між собою. Теорема про існування площини, що паралельна даній площині Через точку поза даною площиною можна провести площину, паралельну даній, і до того ж тільки одну. ВЛАСТИВОСТІ: |
||
|
паралельна цій площині
(b||, bβ) β || |
перетинає її по прямій, паралельній даній прямій
β
b
(b β , b||) a || b |
Якщо дві паралельні площини перетинаються третьою, то прямі перетину паралельні.
( a || b |
Відрізки паралельних прямих, які містяться між двома паралельними площинами, рівні.
(
|
|
|
Паралельне проектування та його властивості |
||
|
h α, A α, А А1|| h, А1 α А1 – паралельна проекція А на площину α. h - проектуюча пряма, α - площина проекції.
Щ |
Властивості паралельного проектування:
|
Зображенням фігури
н фігура, подібна до паралельної проекції даної фігури на деяку площину.
|
|
Перпендикулярність прямих і площин у просторі |
||||||
|
Перпендикулярність прямих |
Перпендикулярність прямої і площин. |
Перпендикулярність площин. |
||||
|
Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.
ОЗНАКА: Якщо дві прямі, які перетинаються, паралельні відповідно двом перпен-дикулярним прямим, то вони теж перпендикулярні.
(a
а1||а,
b1||b,
а1
а1
|
Пряма, яка перетинає площину, називається перпендикулярною до цієї площини, якщо вона перпендикулярна до буд-якої прямої, що лежить у цій площині й проходить через точку перетину. ОЗНАКА: Якщо пряма, перпендикулярна до двох прямих, які лежать у площині і перетинаються , то вона перпендикулярна до даної площини.
(a
ВЛАСТИВОСТІ: 1. Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна й до другої.
(a||b,
α
2. Дві прямі, перпендикулярні до однієї і тієї самої площини, паралельні.
(а
3
(
||
β, а
4
(α |
Д
ОЗНАКА: Якщо площина проходить через пряму, перпендикулярну до другої площини, то площини перпендикулярні.
(b
α
ВЛАСТИВІСТЬ:
Я площині.
а
|
||||
|
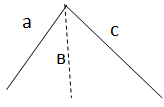
Перпендикуляр та похила у просторі |
|
|||||
|
ОЗНАЧЕННЯ |
Перпендикуляром, опущеним з даної точки на дану площину, називається відрізок, що сполучає дану точку з точкою площини і лежить на прямій, перпендикулярній площині . Основа перпендикуляра – кінець цього відрізка, який лежить у площині (т.С) Відстанню від точки до площини називається довжина перпендикуляра, опущеного з цієї точки на площину.
П Основа похилої – кінець відрізка, що лежить у площині (т.В). Проекцією похилої називається відрізок, який сполучає основи перпендикуляра і похилої, проведених з однієї і тієї самої точки(СВ). Відстанню від прямої до паралельної їй площини називається відстань від будь-якої точки цієї прямої до площини. Відстанню між паралельними площинами називається відстань від будь-якої точки однієї площини до другої площини. |
|
||||
|
ВЛАСТИВОСТІ |
П AD=AB DC=CD
|
П АВ > AC |
З AC>AD CB>BD |
|
||
|
Теорема про три перпендикуляри |
|
|||||
|
Якщо пряма , проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до похилої.
(АВ І навпаки, якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна до проекції похилої.
(АВ
|
|
|||||
|
Многогранники |
|
|
Двогранним кутом називається фігура, утворена двома півплощинами із спільною прямою, що їх обмежує. Півплощини називаються гранями, а пряма, що їх обмежує, - ребром двогранного кута. Площина перпендикулярна до ребра двогранного кута, перетинає його грані по двом пів прямим. Кут, утворений цими пів прямими, називається лінійним кутом двогранного кута. За міру двогранного кута приймається міра відповідного йому лінійного кута
Якщо
φ – лінійний кут двогранного кута, то
0º
|
Двогранний кут
Лінійний кут
двогранного кута |
|
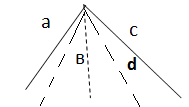
Тригранним кутом (аbс)називається фігура, яка складається з трьох плоских кутів (аb), (bс), (ас). Ці кути називаються гранями тригранного кута, а їх сторони – ребрами. Спільна вершина плоских кутів називається вершиною тригранного кута. Двогранні кути, утворені гранями тригранного кута, називаються двогранними кутами тригранного кута. |
Тригранний кут
Багатогранний кут |
|
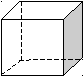
Многогранник – це таке тіло, поверхня якого складається із скінченої кількості плоских многокутників. Многогранник називається опуклим, якщо він лежить по один бік від площини кожного з плоских многокутників на його поверхні. Спільна частина такої площини і поверхні опуклого многогранника називається гранню. Грані опуклого многогранника є плоскими опуклими многокутниками. Сторони граней називаються ребрами многогранника, а вершини – вершинами многогранника. Найпростішими многогранниками є призма (паралелепіпед, куб, піраміда.) |
Многогранники
ребра
грань
вершини |
|
Опуклий многогранник називається правильним, якщо його грані є правильними многогранниками з однією й тією самою кількістю сторін, а в кожній вершині многогранника збігається одне й те ж саме число ребер. |
|


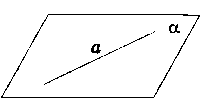
 Прямою
і площиною, які перетинаються
Прямою
і площиною, які перетинаються





 кщо
,
,
кщо
,
,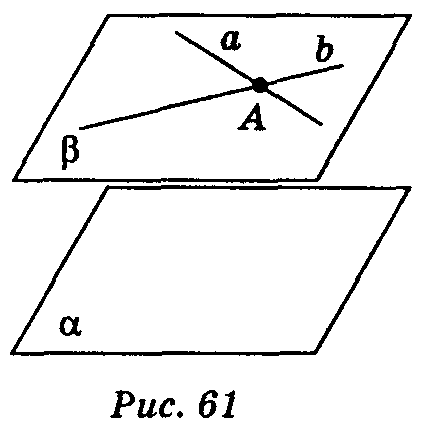 b,
а
b,
а



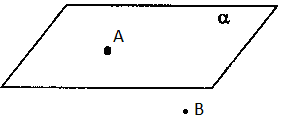
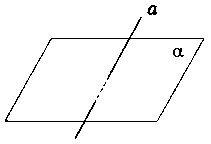 аслідок:
Площина
і пряма, яка не лежить на ній, або
аслідок:
Площина
і пряма, яка не лежить на ній, або

 ерез
будь яку точку простору, яка не лежить
на даній прямій, можна провести пряму,
паралельну даній, і тільки одну.
ерез
будь яку точку простору, яка не лежить
на даній прямій, можна провести пряму,
паралельну даній, і тільки одну.
 .
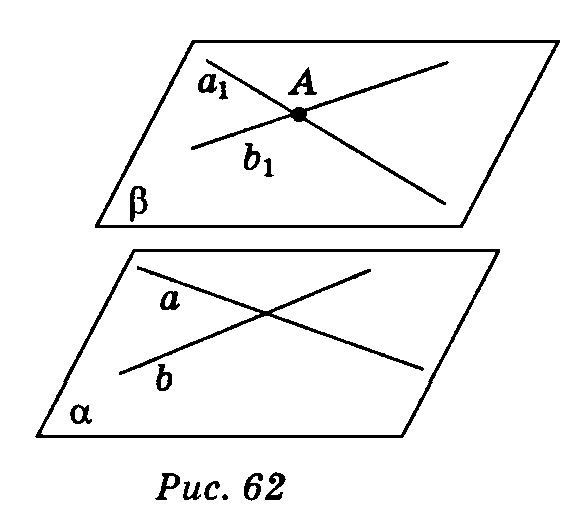
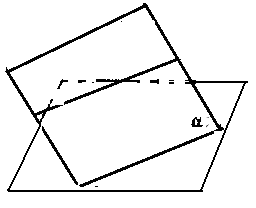
Якщо дві прямі, які перетинаються,
однієї площини відповідно паралельні
двом прямим другої площини, то ці
площини паралельні.
.
Якщо дві прямі, які перетинаються,
однієї площини відповідно паралельні
двом прямим другої площини, то ці
площини паралельні.
||
β, β,
,
b
β, a)
||
β, β,
,
b
β, a)
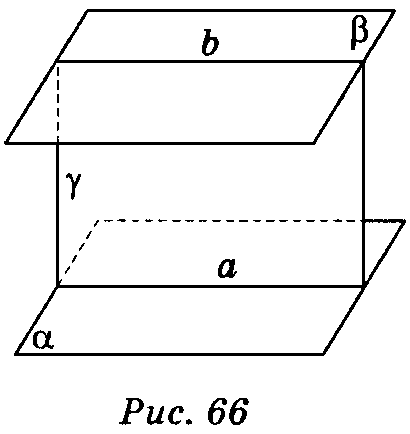
 1
||
2,
a ||
b)
A1A2
= B1В2
1
||
2,
a ||
b)
A1A2
= B1В2
 азивається
будь-яка
азивається
будь-яка


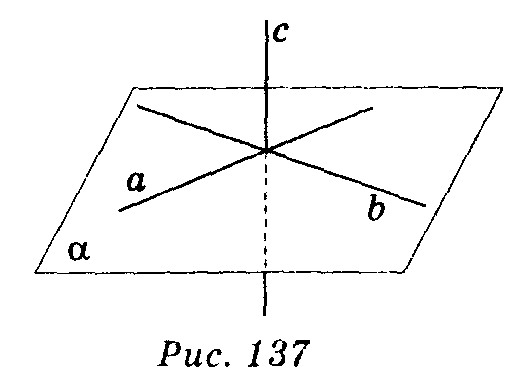 .
Пряма, яка перпендикулярна однієї з
двох паралельних площин, перпендикулярна
і іншій площині.
.
Пряма, яка перпендикулярна однієї з
двох паралельних площин, перпендикулярна
і іншій площині.
 .
Дві площини, які перпендикулярні
одній і тій самій прямій, паралельні
між собою.
.
Дві площини, які перпендикулярні
одній і тій самій прямій, паралельні
між собою.
 ві
площини,
що перетинаються, називаються
перпендикулярними,
якщо третя площина, проведена
перпендикулярно до лінії перетину
цих площин, перетинає їх по
перпендику-лярним прямим.
ві
площини,
що перетинаються, називаються
перпендикулярними,
якщо третя площина, проведена
перпендикулярно до лінії перетину
цих площин, перетинає їх по
перпендику-лярним прямим.
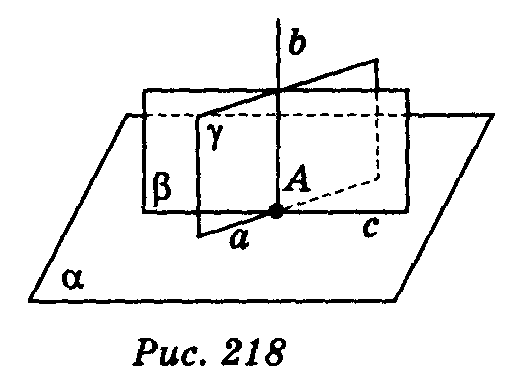 кщо
площини перпендикулярні, то пряма,
яка лежить в одній з них і перпендикулярна
лінії перетину площин, перпендикулярна
іншій
кщо
площини перпендикулярні, то пряма,
яка лежить в одній з них і перпендикулярна
лінії перетину площин, перпендикулярна
іншій
 (α
(α

 охилою,
проведеною з даної точки до даної
площини, називається будь-який
відрізок, який сполучає дану точку з
точкою площини і не є перпендикуляром
до площини (АВ).
охилою,
проведеною з даної точки до даної
площини, називається будь-який
відрізок, який сполучає дану точку з
точкою площини і не є перпендикуляром
до площини (АВ). охилі
до площини, які проведені з однієї
точки,
рівні тоді і тільки тоді, коли рівні
їх проекції.
охилі
до площини, які проведені з однієї
точки,
рівні тоді і тільки тоді, коли рівні
їх проекції.
 ерпендикуляр
завжди менший за будь-яку похилу, яка
буде проведена до площини з тієї ж
самої точки.
ерпендикуляр
завжди менший за будь-яку похилу, яка
буде проведена до площини з тієї ж
самої точки. двох похилих, які проведені з однієї
точки, більше та, в якій більша проекція.
двох похилих, які проведені з однієї
точки, більше та, в якій більша проекція.