Решение типовых примеров

1

Рис. 1.8

. Представить формулой функцию, заданную схемой

Р

Рис. 2.4

ешение. Имеем: Отсюда

2. Построить схему, реализующую функцию

Решение. Положим Схема, реализующая функцию, выглядит так:

3

Рис. 1.9

. Упростить схему (рис. 1.10).

Р

Рис. 1.10

ешение. Требуется построить схему с меньшим числом функциональных элементов, реализующую ту же функцию Для этого выразим формулой и упростим формулу. Имеем:

Рис. 1.11

Следовательно, функция может быть реализована схемой из 2 функциональных элементов (рис. 1.11).

(1)

Пусть V – произвольное множество, V² – множество всех его двухэлементных подмножеств, т.е. множество неупорядоченных пар {а, b}, где а, b  V. Пара (V, E), где Е – произвольное подмножество V², называется графом (неориентированным графом). При этом элементы множества V называются вершинами графа, элементы множества E – ребрами. Множества вершин и ребер графа G обозначаются символами V(G) и E(G) соответственно. Вершины и ребра графа называются его элементами. В дальнейшем рассматриваются только конечные графы, т.е. множество E предполагается конечным. Число | V(G) | вершин называется его порядком и обозначается через |G|. Если |G| = п, |E(G)| = т, то G называют (п, т)-графом.

(2)

Очевидно, что отношение изоморфизма графов является эквивалентностью, т.е. оно симметрично, рефлексивно и транзитивно. Следовательно, все графы разбивается на классы так, что графы из одного класса попарно изоморфны, а графы из разных классов не изоморфны. Изоморфные графы естественно отождествлять, т.е. считать совпадающими (их можно изобразить одним рисунком). Они могли бы различаться конкретной природой своих элементов, но именно это игнорируется при введении понятия графа. Класс изоморфных графов принято называть абстрактным графом.

(3)

Д

Рис. 2.1 Рис. 2.2 Рис. 2.3

ва ребра называются смежными, если они имеют общий конец. Вершина е и ребро v называются инцидентными, если v является концом ребра е, и не инцидентными в противном случае. Графы удобно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. При этом точки соответствуют вершинам графа, а соединяющие пары точек линии – ребрам. В качестве иллюстрации рассмотрим граф G, изображенный на рис. 2.1.

Это (5, 6)-граф, V(G) = {1, 2, 3, 4, 5}, E(G) = {{1, 2}, {1, 5}, {2,3}, {2, 4}, {2, 5}, {4, 5}}. Вершины 1и 2 смежны, а 1 и 3 не смежны. Вершина 1 и ребро {1, 2} инцидентны.

Иногда в графах допускается наличие петель, т.е. ребер {а, а} (рис. 2.2), и кратных ребер, т.е. ребро {а, b} учитывается несколько раз (рис. 2.3). Мы будем рассматривать графы без петель и кратных ребер.

Ориентированный граф – это пара (V, А), где V – множество вершин, А – множество ориентированных ребер (или дуг), т.е. упорядоченных пар (u, v), где u, v  V. При этом и называется началом дуги, v – концом. На рисунке дуги отмечаются стрелками, указывающими направление от начала к концу (рис. 2.4).

(4)

Приведем примеры некоторых графов специального вида. Граф G называется полным, если любые две его вершины смежны, т.е. E(G) = (V(G))⁽²⁾. Полный граф порядка п обозначается символом К_п, в нем ребер. На рис. 2.5 изображены графы К_п, .

Г

Рис. 2.5

раф называется пустым, если в нем нет ребер. Пустой граф порядка п обозначается О_п. Красивыми примерами являются графы пяти платоновых тел (т.е. правильных многогранников): тетраэдра, куба, октаэдра, додекаэдра, икосаэдра.

(5)

Набор подмножеств множества S называется покрытием множества S, если объединение этих множеств совпадает с S. Покрытие называется разбиением, если никакие два из входящих в него множеств не пересекаются.

(6)

Граф называется двудольным, если существует такое разбиение множества его вершин на две части (доли), что концы каждого ребра принадлежат разным частям. Если при этом любые две вершины, входящие в разные доли, смежны, то граф называется полным двудольным. Полный двудольный граф, доли которого состоят из p и из q вершин обозначается символом при р = 1 получаем звезду . На рис. изображены звезда и полный двудольный граф .

З аметим, что одна из долей двудольного графа может быть пустой. Так, О₁ – двудольный граф с одной пустой долей, О₂ можно трактовать как двудольный граф с двумя одновершинными долями или как двудольный граф, одна из долей которого содержит две вершины, а другая является пустым множеством.

(7)

Графы, которые получаются один из другого изменением наименований вершин, называются изоморфными. Пусть G и Н – графы, а – биекция. Если для любых вершин и и v графа G их образы и смежны в Н тогда и только тогда, когда и и v смежны в G, то эта биекция называется изоморфизмом графа G на граф Н. Если такой изоморфизм существует, то мы пишем и говорим, что графы G и Н изоморфны.

Пример 1. Графы, представленные на рис. изоморфны, указана соответствующая изоморфизмам нумерация вершин. Графы на след. рис. неизоморфны (например, вследствие того, что в первом графе есть циклы из трех ребер, а во втором их нет).

(8)

П

Рис. 2.12

роизведением графов называется граф, для которого – декартово произведение множеств вершин исходных графов, а E(G) определяется следующим образом: вершины (и₁, и₂) и (v₁, v₂) в графе G смежны тогда и только тогда, когда или и₁ = v₁, а и₂ и v₂ смежны в G₂, или и₂ = v₂, а и₂ и v₂ смежны в G₁ (рис. 2.12). Очевидно, что ,

.

С помощью операции произведения можно определить п-мерный куб рекуррентно: . Покажем, что это определение совпадает с данным ранее. Действительно, . Вершины графа можно представить векторами длины п из 0 и 1 таким образом, что две вершины будут смежны тогда и только тогда, когда соответствующие векторы различаются в одной координате.

(9)

Д

Рис. 2.13

ля произвольного графа G следующим образом определяется дополнительный граф (или дополнение) : , и две несовпадающие вершины смежны в тогда и только тогда, когда они не смежны в G: (рис. 2.13). Граф, изоморфный своему дополнению, называется самодополнительным.

(10)

Число ребер, инцидентных некоторой вершине v, называется степенью вершины.

(11)

Доказать, что сумма степеней всех вершин графа равно удвоенному числу ребер (лемма о рукопожатиях): . Решение. Рассмотрим сумму степеней всех вершин графа. Каждое ребро вносит в эту сумму 1 два раза (оно учитывается в степенях двух вершин). Поэтому сумма степеней всех вершин графа равно удвоенному числу ребер.

(13)

Г

Рис. 2.14

раф называется связным, если любые две несовпадающие вершины в нем соединены маршрутом.

(14)

(15)

Путь называется простым, если все его вершины, кроме, может быть, крайних, различны. Путь называется цепью, если все его ребра различны, и простой цепью, если все его вершины различны. Путь называется циклическим, если . Циклическая цепь называется циклом, а циклическая простой путь – простым циклом. Простую цепь, имеющую п вершин, будем обозначать C_n, простой цикл – Z_n. Число l ребер в пути называется его длиной.

(16)

В связном графе любые две простые цепи максимальной длины имеют общую вершину. Решение. Предположим, что у двух простых цепей и максимальной длины нет общих вершин. Возьмем произвольно по одной вершине из каждой цепи и . Так как граф связный, то существует путь из в . Выберем из отрезков цепей от до и от до тот, длина которого не меньше . Аналогично для . Составим новую простую цепь из этих отрезков и простой цепи, соединяющей и , ее длина больше , что противоречит тому, что исходные цепи максимальны.

(17)

Пусть G – граф, а и и v – две его несовпадающие вершины. Длина кратчайшего (и, v)-маршрута (он, естественно, является простой цепью) называется расстоянием между вершинами и и v и обозначается через d(u, v). Положим еще d(u, и) = 0. Для фиксированной вершины и величина

называется эксцентриситетом вершины и. Максимальный из всех эксцентриситетов вершин графа называется диаметром графа G и обозначается через d(G). Тем самым,

.

(18)

Вершина называется центральной, если .Вершина v называется периферийной, если .

(20)

Пусть G – граф порядка п. Занумеруем его вершины: . Определим матрицу А = А(G) размера п  п следующим образом:

А(G) называется матрицей смежности графа G.

(23)

Пусть -граф, . Определим матрицу I = I(G) размера п  т, положив

Матрица I называется матрицей инцидентности графа G. В каждом ее столбце ровно две единицы, одинаковых столбцов нет.

(24)

Рангом графа называется ранг его матрицы смежности.

(25)

Теорема. Для каждого связного графа G верно неравенство . Доказательство. Пусть . Рассмотрим матрицу смежности А(G), причем выберем нумерацию вершин так, чтобы вершины одной из диаметральных цепей имели номера 1, 2, …, d+1: – диаметральная цепь. Очевидно, что является клеточной матрицей, в левом верхнем углу которой расположена матрица смежности А порожденного подграфа Этот подграф является простой цепью, следовательно,

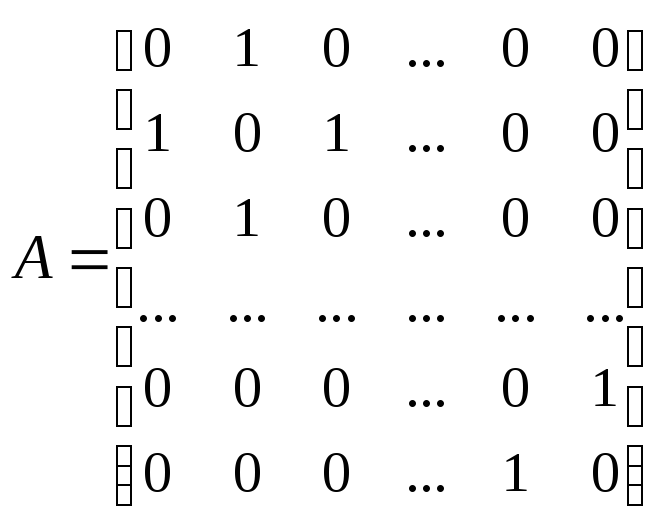
– симметрическая матрица порядка d + 1, все элементы которой, за исключением двух ближайших к диагонали полос единиц, равны нулю. минор порядка d матрицы А, остающийся после вычеркивания первого столбца и последней строки, равен 1. Следовательно, . Теорема доказана.

Теорема. Для любого графа выполняется неравенствоДоказательство проведем индукцией по числу вершин п. При п = 1 получаем граф, состоящий из одной вершины, соответственно без ребер: . Неравенство выполнено. Предположим, что при любом количестве вершин, меньшем п, утверждение верно и докажем его для графа с п вершинами. Обозначим их . Обозначим через подграф графа , порожденный вершинами . Тогда по предположению индукции. Пусть – количество ребер, вершин, компонент связности графа ; – графа ; k – количество ребер графа , не являющихся ребрами графа , т.е. степень вершины . Тогда . Возможны два случая.

а) , следовательно, вершина – изолированная. При этом . Следовательно, , .

б) . Если при этом все k ребер, инцидентных вершине , соединяют ее с различными компонентами связности графа , то , в остальных случаях . Таким образом,

. В итоге получаем . Теорема доказана.

Следствие. Для связного графа выполняется неравенство .

(27)

Теорема. Для любого графа либо он сам, либо его дополнение является связным. Доказательство. Пусть G – несвязный граф. А – одна из его компонент связности. Положим В = VG \ VA. Возьмем произвольную вершину и графа А. Тогда для любой вершины v из из множества вершин В в дополнительном графе есть ребро uv. Следовательно, произвольная вершина из В соединена с и. Если и₁ – отличная от и вершина графа А, то для любой вершины v из множества вершин В в дополнительном графе также найдется ребро u₁v. Таким образом найдется путь из вершины и в вершину u₁ (через вершину v). Следовательно, из вершины и в графе достижима любая вершина, а значит, граф является связным. Теорема доказана. Утверждение. Пусть G – связный граф, . Тогда: а)Если ребро е принадлежит какому-либо циклу графа G, то граф связен; б)!!! Если ребро е не входит ни в какой цикл, то граф имеет ровно две компоненты связности.

(30)

Связный граф без циклов называется деревом. Любой граф без циклов называется ациклическим (или лесом). Таким образом, компонентами связности леса являются деревья. На рис. 2.31 изображен лес, каждая компонента связности его является деревом. Теорема. Связный граф является деревом тогда и только тогда, когда число его вершин на единицу больше числа его ребер, т.е. .

Доказательство. Необходимость. Заметим, что если граф G – дерево, то он имеет хотя бы одну вершину степени 1 (висячую вершину). Действительно, предположим, что все вершины имеют степень, не меньшую 2. Возьмем произвольную вершину, обозначим ее . Из нее выходит по крайней мере два ребра. Найдется вершина такая, что . Так как степень вершиныне меньше 2, то найдется вершина , отличная от , такая, что , и так далее. Так как число вершин конечно, то в этой последовательности вершин найдутся совпадающие, и мы получим цикл, что противоречит определению дерева. Следовательно, висячая вершина существует.

Далее доказательство проведем индукцией по числу вершин п. При п = 1 число ребер равно 0 и утверждение верно. Предположим оно верно при любом количестве вершин, меньшем п. Рассмотрим граф G с п вершинами. Среди них есть висячая. Рассмотрим подграф G', порожденный множеством остальных вершин. Для него по индукционному предположению . Кроме того, . Следовательно, . Необходимость доказана.

Достаточность. Пусть для связного графа G выполняется условие . Для того, чтобы доказать, что G является деревом, нужно показать лишь отсутствие циклов. Предположим, что циклы есть, тогда удаление одного ребра е из цикла не нарушает связности, граф тоже связный. Следовательно, для него выполняется неравенство . Но , следовательно, и значит, , что противоречит условию. Следовательно, G является связным графом без циклов, т.е. деревом. Теорема доказана.