
(1)
Высказыванием
называется некоторое повествовательное
утверждение, про которое можно однозначно
сказать, истинно оно или ложно. Всякое
высказывание является либо истинным,
либо ложным (закон
исключения третьего).
Никакое высказывание не может быть
одновременно истинным и ложным (закон
противоречия).
Отрицанием
высказывания
![]() (обозначается
(обозначается ![]() или
или
![]() )
называется высказывание, утверждающее,
что высказывание
)
называется высказывание, утверждающее,
что высказывание
![]() не выполняется. Каково бы ни было
высказывание
не выполняется. Каково бы ни было
высказывание
![]() ,
из двух высказываний
,
из двух высказываний
![]() и
и ![]() одно является
истинным, а другое ложным. Высказывание
одно является
истинным, а другое ложным. Высказывание
![]() )
(или
)
(или
![]() )
называется
двойным
отрицанием
высказывания
)
называется
двойным
отрицанием
высказывания
![]() .
Имеет место равенство
.
Имеет место равенство ![]() )
=
)
=![]() (закон
двойного отрицания).
Повествовательное утверждение, зависящее
от некоторой переменной
(закон
двойного отрицания).
Повествовательное утверждение, зависящее
от некоторой переменной
![]() и становящееся при конкретных значениях
и становящееся при конкретных значениях
![]() высказыванием, называется неопределенным
высказыванием
(или предикатом).
высказыванием, называется неопределенным
высказыванием
(или предикатом).
Для
неопределенного высказывания можно
построить
таблицу истинности.
В таблице для конкретных значений
переменной
![]() указывается, истинно высказывание или
ложно при этом
указывается, истинно высказывание или
ложно при этом
![]() .
Символы “”
и “”
называются квантором
всеобщности и
квантором
существования
соответственно.
.
Символы “”
и “”
называются квантором
всеобщности и
квантором
существования
соответственно.
Во многих вопросах математики возникает необходимость строить отрицание высказывания, выраженного с помощью кванторов.
Отрицания
высказываний “![]() ”
и “
”
и “![]() ”.
Имеет место равенство
”.
Имеет место равенство ![]()
![]()
![]() .
Действительно, утверждение “неверно,
что для всех
.
Действительно, утверждение “неверно,
что для всех
![]()
![]() ”
– это то же самое, что “для какого-нибудь
”
– это то же самое, что “для какого-нибудь
![]() не
не
![]() ”.
Аналогично справедливо равенство
”.
Аналогично справедливо равенство
![]()
![]()
![]() ,
так как утверждение “неверно, что
существует
,
так как утверждение “неверно, что
существует
![]() ,
для которого
,
для которого
![]() ”
равносильно следующему: “для всех
”
равносильно следующему: “для всех
![]() не
не
![]() ”.
Таким образом, чтобы построить отрицание
высказывания, содержащего кванторы,
надо кванторы
”.
Таким образом, чтобы построить отрицание
высказывания, содержащего кванторы,
надо кванторы
![]() заменить на
заменить на
![]() ,
а
,
а
![]() на
на
![]() ,
а утверждение, стоящее под знаком
кванторов, заменить на противоположное.
,
а утверждение, стоящее под знаком
кванторов, заменить на противоположное.
1.
Дизъюнкцией
(или логической
суммой)
двух высказываний
![]() и
и
![]() называется высказывание (обозначается
называется высказывание (обозначается
![]() ),
истинное в случае, если хотя бы одно из
высказываний
),
истинное в случае, если хотя бы одно из
высказываний
![]() и
и
![]() истинно.
истинно.
2.
Конъюнкцией
(или логическим
произведением)
двух высказываний
![]() и
и
![]() называется высказывание (обозначается
называется высказывание (обозначается
![]() или
или
![]() ),
истинное тогда и только тогда, когда
оба высказывания
),
истинное тогда и только тогда, когда
оба высказывания
![]() и
и
![]() истинны.
истинны.
3.
Эквиваленцией
двух высказываний
![]() и
и
![]() называется высказывание (обозначается
называется высказывание (обозначается
![]() или
или
![]() ),
истинное тогда и только тогда, когда
оба высказывания
),
истинное тогда и только тогда, когда
оба высказывания
![]() и
и
![]() одновременно истинны или ложны.
одновременно истинны или ложны.
4.
Импликацией
двух высказываний
![]() и
и
![]() называется высказывание (обозначается
называется высказывание (обозначается
![]() или
или
![]() ,
или
,
или
![]() ;
;
![]() называется посылкой,
называется посылкой,
![]() заключением),
ложное в том и только том случае, когда
посылка истинна, а заключение ложно.
Для любых высказываний истинность или
ложность их суммы, произведения,
эквивалентности и импликации определяется
в соответствии с таблицей, называемой
таблицей
истинности логических операций,
в которой приведены значения сложного
высказывания, в зависимости от значений
высказываний
заключением),
ложное в том и только том случае, когда
посылка истинна, а заключение ложно.
Для любых высказываний истинность или
ложность их суммы, произведения,
эквивалентности и импликации определяется
в соответствии с таблицей, называемой
таблицей
истинности логических операций,
в которой приведены значения сложного
высказывания, в зависимости от значений
высказываний
![]() и
и
![]() .
Два высказывания равносильны,
если их таблицы истинности совпадают.
Тождественно
истинные высказывания –
высказывания истинные всегда, независимо
от того, истинны или ложны составляющие
их высказывания. Тождественно истинное
высказывание иначе называют тавтологией.
Тождественно
ложные высказывания –
высказывания ложные всегда, независимо
от истинности или ложности составляющих
их высказываний
.
Два высказывания равносильны,
если их таблицы истинности совпадают.
Тождественно
истинные высказывания –
высказывания истинные всегда, независимо
от того, истинны или ложны составляющие
их высказывания. Тождественно истинное
высказывание иначе называют тавтологией.
Тождественно
ложные высказывания –
высказывания ложные всегда, независимо
от истинности или ложности составляющих
их высказываний
(2)
Свойства операций над высказываниями
1.
а)
![]() (коммутативность
дизъюнкции);
(коммутативность
дизъюнкции);
б)
![]() (коммутативность
конъюнкции);
(коммутативность
конъюнкции);
2.
а)
![]() (ассоциативность
дизъюнкции);
(ассоциативность
дизъюнкции);
б)
![]() (ассоциативность
конъюнкции);
(ассоциативность
конъюнкции);
3.а)
![]() (дистрибутивность дизъюнкции относительно
конъюнкции);
(дистрибутивность дизъюнкции относительно
конъюнкции);
б)
![]() (дистрибутивность конъюнкции относительно
дизъюнкции);
(дистрибутивность конъюнкции относительно
дизъюнкции);
4.
![]() и
и
![]() – законы
де Моргана.
– законы
де Моргана.
5.
![]() ;
;
![]() ;
;
![]() ;
;
6.
![]() (или
(или
![]() )
(закон
исключенного третьего);
)
(закон
исключенного третьего);
![]() (или
(или
![]() (закон
противоречия);
(закон
противоречия);
7.![]() (или
(или
![]() );
);
![]() (или
(или
![]() );
);
![]() (или
(или
![]() );
);
![]() (или
(или
![]() ).
).
(3)
В
дальнейшем в качестве множества
![]() будет использоваться множество
будет использоваться множество
![]() .
Набор
.
Набор
![]() ,
где
,
где
![]() ,
называется булевым
или двоичным
набором
(вектором).
Элементы набора называют компонентами
или координатами.
Число
,
называется булевым
или двоичным
набором
(вектором).
Элементы набора называют компонентами
или координатами.
Число
![]() называют длиной
набора.
Кратко
называют длиной
набора.
Кратко
![]() обозначают
обозначают
![]() или
или
![]() .
Весом (или
нормой)
набора
.
Весом (или
нормой)
набора
![]() называют число его координат, равных
1, т.е.
называют число его координат, равных
1, т.е.
![]() .
Число
.
Число
![]() называют номером
набора
называют номером
набора
![]() .
Множество всех булевых векторов
.
Множество всех булевых векторов
![]() длины
длины
![]() называется
называется
![]() -мерным
кубом. Сами
векторы называются вершинами
-мерным
кубом. Сами
векторы называются вершинами
![]() -мерного
куба. Пусть
-мерного
куба. Пусть
![]() фиксированный
набор чисел из 0 и 1 (
фиксированный
набор чисел из 0 и 1 (![]() ).
Множество всех вершин
).
Множество всех вершин
![]() куба
куба
![]() таких, что
таких, что
![]() ,
называется
,
называется
![]() -мерной
гранью.
-мерной
гранью.
Замечание.
![]() -мерная
грань является
-мерная
грань является
![]() -мерным
подкубом куба
-мерным
подкубом куба
![]() .
.
Расстоянием
(Хемминга)
между вершинами
![]() и
и
![]() куба
куба
![]() называется число координат, в которых
наборы
называется число координат, в которых
наборы
![]() и
и
![]() отличаются друг от друга.
отличаются друг от друга.
Вершины
![]() и
и
![]() куба
куба
![]() – соседние,
если
– соседние,
если
![]() .
.
(4)
Ф
0
0
0
1
1
1
0
1
0
1
![]()
![]()
![]()
![]()
![]()
![]() такая, что
такая, что
![]() ,
называется булевой
функцией (или функцией
алгебры логики) от
,
называется булевой
функцией (или функцией
алгебры логики) от
![]() переменных. Для задания булевой функции
переменных. Для задания булевой функции
![]() требуется указать ее значения на каждом
наборе
требуется указать ее значения на каждом
наборе
![]() .
.
(5)
При
![]() функцию
функцию
![]() можно задать таблицей
можно задать таблицей
![]() (табл. 1.1), называемой таблицей
истинности
функции, в которой наборы
(табл. 1.1), называемой таблицей
истинности
функции, в которой наборы
![]() выписываются в порядке возрастания их
номеров (сверху вниз). При стандартном
расположении наборов (в соответствии
с увеличением их номера), функцию
выписываются в порядке возрастания их
номеров (сверху вниз). При стандартном
расположении наборов (в соответствии
с увеличением их номера), функцию
![]() можно задавать вектором
ее значений
можно задавать вектором
ее значений
![]() (или
(или
![]() ),
где координата
),
где координата
![]() равна значению функции
равна значению функции
![]() в
в
![]() -ой
строке таблицы (
-ой
строке таблицы (![]() ),
т.е. на наборе
),
т.е. на наборе
![]() .
При этом значение переменной
.
При этом значение переменной
![]()
![]() -ой
строке таблицы есть компонента
-ой
строке таблицы есть компонента
![]() набора
набора
![]() ,
которая определяются как соответствующая
,
которая определяются как соответствующая
![]() -я
цифра в записи числа
-я
цифра в записи числа
![]() .
.
Обозначим
через
![]() множество всех булевых функций от
множество всех булевых функций от
![]() переменных, а
переменных, а
![]() множество всех булевых функций.
множество всех булевых функций.
Теорема.
![]() .
.
Доказательство.
Поскольку
функция
![]() задается вектором значений
задается вектором значений
![]() ,
где
,
где
![]() ,
,
![]() ,
то различных булевых функций от
,
то различных булевых функций от
![]() переменных столько же, сколько различных
переменных столько же, сколько различных
![]() -разрядных
двоичных векторов, т.е.
-разрядных
двоичных векторов, т.е.
![]() .
.
В
противном случае переменная
![]() – фиктивная,
т.е. функция
– фиктивная,
т.е. функция
![]() не зависит от
не зависит от
![]() .
.
Процедура удаления (введения) фиктивных переменных
Пусть
переменная
![]() для функции
для функции
![]() –
фиктивная. Тогда для ее удаления
вычеркиваем все строки таблицы, в которых
–
фиктивная. Тогда для ее удаления
вычеркиваем все строки таблицы, в которых
![]() и столбец переменной
и столбец переменной
![]() .
В итоге получаем функцию от
.
В итоге получаем функцию от
![]() переменной.
переменной.
Две
функции
![]() и
и
![]() от разного количества переменных равны,
если одна получается из другой путем
удаления или введения фиктивных
переменных.
от разного количества переменных равны,
если одна получается из другой путем
удаления или введения фиктивных
переменных.
Благодаря введенному понятию конечную совокупность булевых функций можно считать зависящей от одного и того же числа переменных, являющегося объединением множеств переменных всех функций совокупности.
Функции одной переменной
В таблице 1.5 представлены все булевы функции одной переменной.
Функции
![]() и
и
![]() называются соответственно (тождественным)
нулем
и (тождественной)
единицей.
называются соответственно (тождественным)
нулем
и (тождественной)
единицей.
Функция
![]() называется тождественной
функцией и
обозначается
называется тождественной
функцией и
обозначается
![]() .
.
Функция
![]() называется отрицанием
(или инверсией)
называется отрицанием
(или инверсией)
![]() ,
обозначается
,
обозначается
![]() или
или
![]() и читается «не
и читается «не
![]() ».
».
Функции двух переменных
В таблице 1.6 представлены все булевы функции от двух переменных.
Табл. 1.6
Функция
![]() называется конъюнкцией
называется конъюнкцией
![]() и
и
![]() ,
обозначается
,
обозначается
![]() &
&![]() или
или
![]() ,
или
,
или
![]() ,
и часто читается «
,
и часто читается «![]() и
и
![]() ».
».
Функция
![]() называется суммой
по модулю 2
называется суммой
по модулю 2
![]() и
и
![]() ,
обозначается
,
обозначается
![]() или
или
![]() ,
и часто читается «
,
и часто читается «![]() плюс
плюс
![]() ».
».
Функция
![]() называется дизъюнкцией
называется дизъюнкцией
![]() и
и
![]() ,
обозначается
,
обозначается
![]() ,
и часто читается «
,
и часто читается «![]() или
или
![]() ».
Функция
».
Функция
![]() называется стрелкой
Пирса
называется стрелкой
Пирса
![]() и
и
![]() ,
обозначается
,
обозначается
![]() ,
и часто читается «ни
,
и часто читается «ни
![]() ,
ни
,
ни
![]() »
или «ни
»
или «ни
![]() и ни
и ни
![]() ».
В технической литературе ее обычно
называют антидизъюнкцией
или функцией
Вебба (а
также функцией
Даггера).
Функция
».
В технической литературе ее обычно
называют антидизъюнкцией
или функцией
Вебба (а
также функцией
Даггера).
Функция
![]() называется эквиваленцией
(или
эквивалентностью)
называется эквиваленцией
(или
эквивалентностью)
![]() и
и
![]() ,
обозначается
,
обозначается
![]() или
или
![]() ,
или
,
или
![]() ,
и читается «
,
и читается «![]() эквивалентно
эквивалентно
![]() ».
Функция
».
Функция
![]() называется импликацией
называется импликацией
![]() и
и
![]() ,
обозначается
,
обозначается
![]() или
или
![]() ,
и часто читается «
,
и часто читается «![]() имплицирует
имплицирует
![]() »
или «из
»
или «из
![]() следует
следует
![]() ».Функция
».Функция
![]() называется штрихом
Шеффера
называется штрихом
Шеффера
![]() и
и
![]() ,
обозначается
,
обозначается
![]() и часто читается «не
и часто читается «не
![]() или не
или не
![]() »
или «
»
или «![]() и
и
![]() не совместны». В технической литературе
ее обычно называют антиконъюнкцией.
не совместны». В технической литературе
ее обычно называют антиконъюнкцией.
Символы
из множества
![]() ,
в алгебре логики участвующие в обозначениях
элементарных функций, называют логическими
связками.
,
в алгебре логики участвующие в обозначениях
элементарных функций, называют логическими
связками.
(6)
1.
Коммутативность:
![]() ,
где
,
где
![]() .
.
2.
Ассоциативность:
![]() ,
где
,
где
![]() .
.
3. Дистрибутивность
![]() ,
,
![]() ,
,
![]() .
.
4. Законы де Моргана:
а)
![]() ;
б)
;
б)
![]() .
.
5.
Закон двойного отрицания
![]() .
.
6.
Законы поглощения: а)
![]() ;
б)
;
б)
![]() .
.
7.
а)
![]() ;
;
б)
![]() в)
в)
![]() г)
г)
![]() д)
д)
![]() .
.
8.
а)
![]() ;
б)
;
б)
![]() .
.
9.
а)
![]() (склеивание);
(склеивание);
б)
![]() (обобщенное склеивание).
(обобщенное склеивание).
(7)
Функция
![]()
![]() называется двойственной
к функции
называется двойственной
к функции
![]() .
.
Табл. 1.8
Замечание.
Таблица двойственной функции получается
из таблицы функции
![]() инвертированием столбца значений
функции и его переворачиванием (см.
табл. 1.8).
инвертированием столбца значений
функции и его переворачиванием (см.
табл. 1.8).
Из
определения двойственности следует,
что
![]() ,
т.е. функция
,
т.е. функция
![]() является двойственной к
является двойственной к
![]() (свойство
взаимности).
Функция
(свойство
взаимности).
Функция
![]() называется самодвойственной,
если
называется самодвойственной,
если
![]() .
Например, самодвойственными являются
функции
.
Например, самодвойственными являются
функции
![]() и
и
![]() .
Обозначим через
.
Обозначим через
![]() все различные символы переменных,
встречающихся в множествах
все различные символы переменных,
встречающихся в множествах
![]() .
.
Теорема.
Если
![]() ,
то
,
то
![]() .
.
Доказательство.
![]()
![]()
![]()
![]()
![]() .
.
Следствие.
(Принцип
двойственности.)
Если формула
![]() реализует функцию
реализует функцию
![]() ,
то формула
,
то формула
![]() реализует функцию
реализует функцию
![]() .
Эту формулу называют формулой,
двойственной
к
.
Эту формулу называют формулой,
двойственной
к
![]() ,
и обозначают
,
и обозначают
![]() .
.
(8 и 9)
Ведем
обозначение
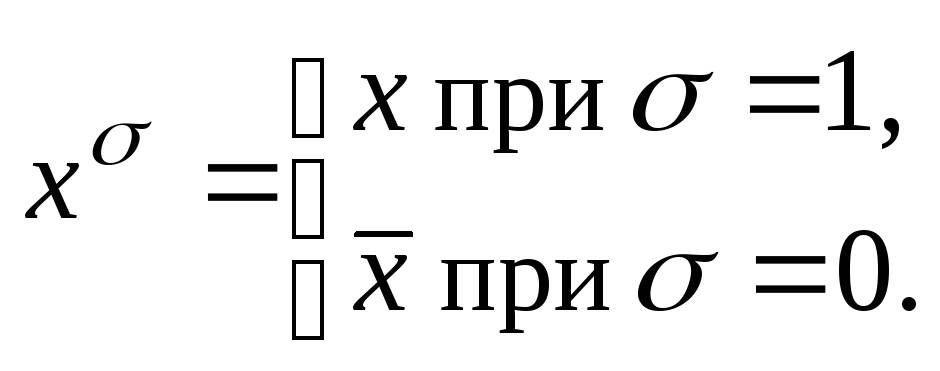
Выражение
![]() ,
где
,
где
![]() какой-либо двоичный набор, причем среди
переменных
какой-либо двоичный набор, причем среди
переменных
![]() могут быть совпадающие, называется
элементарной
конъюнкцией.
Выражения вида
могут быть совпадающие, называется
элементарной
конъюнкцией.
Выражения вида
![]() называют буквами.
Число букв в элементарной конъюнкции
называют рангом
элементарной конъюнкции. Элементарная
конъюнкция – правильная,
если в нее каждая переменная входит не
более одного раза (включая и отрицание
переменной);
называют буквами.
Число букв в элементарной конъюнкции
называют рангом
элементарной конъюнкции. Элементарная
конъюнкция – правильная,
если в нее каждая переменная входит не
более одного раза (включая и отрицание
переменной);
– полная
относительно
переменных
![]() ,
если в нее каждая переменная (или ее
отрицание) входит ровно один раз;
,
если в нее каждая переменная (или ее
отрицание) входит ровно один раз;
– монотонная, если она не содержит отрицаний переменных.
Формула
вида
![]() ,
где
,
где
![]() попарно различные элементарные
конъюнкции, называется дизъюнктивной
нормальной формой
(сокращенно ДНФ). Число
попарно различные элементарные
конъюнкции, называется дизъюнктивной
нормальной формой
(сокращенно ДНФ). Число
![]() называется длиной ДНФ.
называется длиной ДНФ.
Теорема.
Каждую булеву функцию
![]() при любом
при любом
![]() (
(![]() )
можно представить в виде
)
можно представить в виде
 Это
представление называется разложением
функции по переменным
Это
представление называется разложением
функции по переменным
![]() .
Доказательство.
Заметим, что
.
Доказательство.
Заметим, что
![]() Далее рассмотрим произвольный набор
Далее рассмотрим произвольный набор
![]() и покажем, что левая и правая часть
формулы (
и покажем, что левая и правая часть
формулы (![]() )
принимают на нем одно и то же значение.
)
принимают на нем одно и то же значение.
Левая
часть дает
![]() ,
а правая
,
а правая
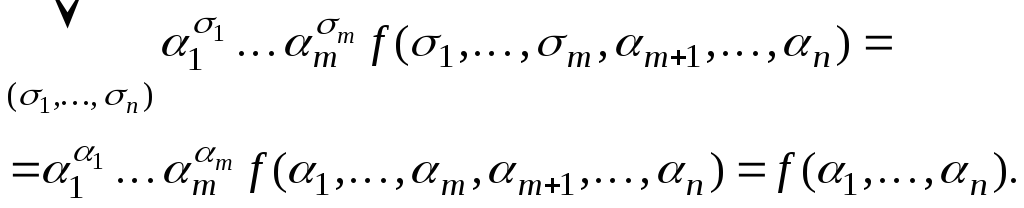 Следствие
1. Разложение
по переменной
Следствие
1. Разложение
по переменной
![]() .
Пусть
.
Пусть
![]() .
Тогда
.
Тогда
![]() Следствие
2. Разложение
по всем переменным.
Пусть
Следствие
2. Разложение
по всем переменным.
Пусть![]() .
Тогда
.
Тогда
![]()
При
![]() получаем выражение
получаем выражение
 т.е.
т.е.
 Разложение
(**) носит название
совершенной дизъюнктивной нормальной
формы
(СДНФ). Замечания
1. Поскольку
существует взаимно однозначное
соответствие между таблицей истинности
Разложение
(**) носит название
совершенной дизъюнктивной нормальной
формы
(СДНФ). Замечания
1. Поскольку
существует взаимно однозначное
соответствие между таблицей истинности
![]() и СДНФ функции
и СДНФ функции
![]() ,
то СДНФ функции единственна. 2.
Единственная функция, не имеющая СДНФ,
– константа 0. 3.
Длина СДНФ функции
,
то СДНФ функции единственна. 2.
Единственная функция, не имеющая СДНФ,
– константа 0. 3.
Длина СДНФ функции
![]() равна числу наборов, на которых функция
принимает значение, равное 1.
равна числу наборов, на которых функция
принимает значение, равное 1.
Теорема.
Любая логическая операция может быть
выражена через операции отрицания и
конъюнкции. Доказательство.
Выразим дизъюнкцию через операции
отрицания и конъюнкции, используя закон
двойного отрицания и закон де Моргана:
![]() .
Найдя СДНФ или СКНФ данной операции и
заменив в них дизъюнкцию через операции
отрицания и конъюнкции, получим формулу,
содержащую только операции отрицания
и конъюнкции.
.
Найдя СДНФ или СКНФ данной операции и
заменив в них дизъюнкцию через операции
отрицания и конъюнкции, получим формулу,
содержащую только операции отрицания
и конъюнкции.
Процедура упрощения д. н. ф. (алгоритм Блейка)
1.
Удаление элементарной конъюнкции,
которая представима в виде
![]() .
.
![]() – реализует функцию
– реализует функцию
![]() и если
и если
![]() – тоже реализует функцию
– тоже реализует функцию
![]() ,
тогда мы можем отбросить
,
тогда мы можем отбросить
![]() .
.
![]() .
2. Удаление множителя. Для двух д. н. ф.
.
2. Удаление множителя. Для двух д. н. ф.
![]() и
и
![]() таких, что
таких, что
![]() ,
,
![]() .
Д. н. ф., которую нельзя упростить с
помощью вышеприведенных методов,
называется тупиковой.
Примеры:
Для функции
.
Д. н. ф., которую нельзя упростить с
помощью вышеприведенных методов,
называется тупиковой.
Примеры:
Для функции
![]() д. н. ф.
д. н. ф.
![]() – не тупиковая, а
– не тупиковая, а
![]() – тупиковая.
– тупиковая.
Метод Нельсона
1.
По
![]() строят СКНФ. Например, для
строят СКНФ. Например, для
![]()
СКНФ
=![]() .
.
2. Раскрывют скобки.
![]()
![]()
![]()
![]() 3.
Производят упрощение по следующим
правилам:
3.
Производят упрощение по следующим
правилам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Метод Квайна
1.
По
![]() строим СДНФ. Например, для функции
строим СДНФ. Например, для функции
![]() .
СДНФ=
.
СДНФ=![]() .
.
2. Применяем операцию неполного склеивания
![]() .
.
3.
После того как такая операция применена
к каждой паре конъюнкций из СДНФ, к
которой она применима, с помощью операции
поглощения (![]() )
удаляем те конъюнкции ранга
)
удаляем те конъюнкции ранга
![]() ,
которые можно удалить таким образом. В
итоге получаем некоторую д. н. ф.
,
которые можно удалить таким образом. В
итоге получаем некоторую д. н. ф.
![]() .
.
4.
Если проведено
![]() этапов, то на
этапов, то на
![]() -м
этапе операции неполного склеивания и
поглощения применяются к конъюнкции
ранга
-м
этапе операции неполного склеивания и
поглощения применяются к конъюнкции
ранга
![]() д. н. ф.
д. н. ф.
![]() .
Получаем д. н. ф.
.
Получаем д. н. ф.
![]() .
.
Алгоритм
завершается, если
![]() .
.
(10)
Полиномом
Жегалкина
(полиномом по модулю 2) от переменных
![]() называется выражение вида
называется выражение вида
![]() где
где
![]() .
.
Наибольший
из рангов элементарных конъюнкций
входящих в полином, называется степенью
этого
полинома. Степень полинома 0 принимается
равной
![]() .
Число слагаемых в формуле полинома
называется длиной
полинома.
Теорема.
Каждая функция из
.
Число слагаемых в формуле полинома
называется длиной
полинома.
Теорема.
Каждая функция из
![]() представляется в виде полинома Жегалкина
и это представление единственно.
Доказательство.
Существование полинома для каждой
булевой функции, отличной от константы
0, следует из того, что ее СДНФ применением
равенств
представляется в виде полинома Жегалкина
и это представление единственно.
Доказательство.
Существование полинома для каждой
булевой функции, отличной от константы
0, следует из того, что ее СДНФ применением
равенств
![]()
сводится
к полиному. Для доказательства
единственности подсчитаем число
полиномов Жегалкина от переменных
![]() ,
т.е. число выражений вида
,
т.е. число выражений вида
![]() .
.
Число
слагаемых
![]() в указанной сумме равно количеству
подмножеств
в указанной сумме равно количеству
подмножеств
![]() из
из
![]() чисел
чисел
![]() ,
т.е.
,
т.е.
![]() .
Каждому полиному в соответствие можно
поставить вектор
.
Каждому полиному в соответствие можно
поставить вектор
![]() длины
длины
![]() ,
компонентами которого являются числа
,
компонентами которого являются числа
![]() ,
равные 0 или 1. Следовательно, искомое
число полиномов равно
,
равные 0 или 1. Следовательно, искомое
число полиномов равно
![]() ,
т.е. числу всех булевых функций от
переменных
,
т.е. числу всех булевых функций от
переменных
![]() .
Следствие.
Из доказанной теоремы вытекает
единственность представления булевой
функции посредством полинома Жегалкина.
.
Следствие.
Из доказанной теоремы вытекает
единственность представления булевой
функции посредством полинома Жегалкина.
Приведем основные методы построения полиномов Жегалкина от заданной функции.
1. Метод неопределенных коэффициентов. Пусть – искомый полином Жегалкина, реализующий заданную функцию . Запишем его в виде
![]() Вектор
Вектор
![]() длины
длины
![]() назовем вектором
коэффициентов полинома
назовем вектором
коэффициентов полинома
![]() .
Найдем его компоненты. Для этого заметим,
что если переменным
.
Найдем его компоненты. Для этого заметим,
что если переменным
![]() придать значения
придать значения
![]() из
из
![]() -ой
строки таблицы, то значение
-ой
строки таблицы, то значение
![]() будет равно сумме
будет равно сумме
![]() с компонентами вектора
с компонентами вектора
![]() ,
соответствующими ненулевым конъюнкциям
,
соответствующими ненулевым конъюнкциям
![]() (
(![]() ).
В итоге получим систему из
).
В итоге получим систему из
![]() уравнений с
уравнений с
![]() неизвестными, имеющую единственное
решение. Решив ее, находим коэффициенты
полинома
неизвестными, имеющую единственное
решение. Решив ее, находим коэффициенты
полинома
![]() .
2. Метод,
основанный на преобразовании формул
над множеством связок
.
2. Метод,
основанный на преобразовании формул
над множеством связок
![]() .
Строят некоторую формулу
.
Строят некоторую формулу
![]() над множеством связок
над множеством связок
![]() ,
реализующую данную функцию
,
реализующую данную функцию
![]() .
Затем заменяют всюду подформулы вида
.
Затем заменяют всюду подформулы вида
![]() на
на
![]() ,
раскрывают скобки, пользуясь дистрибутивным
законом
,
раскрывают скобки, пользуясь дистрибутивным
законом
![]() ,
и применяют эквивалентности
,
и применяют эквивалентности
![]() .
.
Пример.
Построить полином Жегалкина функции
![]() .
.
Решение.
1. (Метод неопределенных коэффициентов).
Запишем искомый полином в виде
![]()
Табл. 1.11
|
|
|
|
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
![]()
![]()
![]()
Получаем систему уравнений
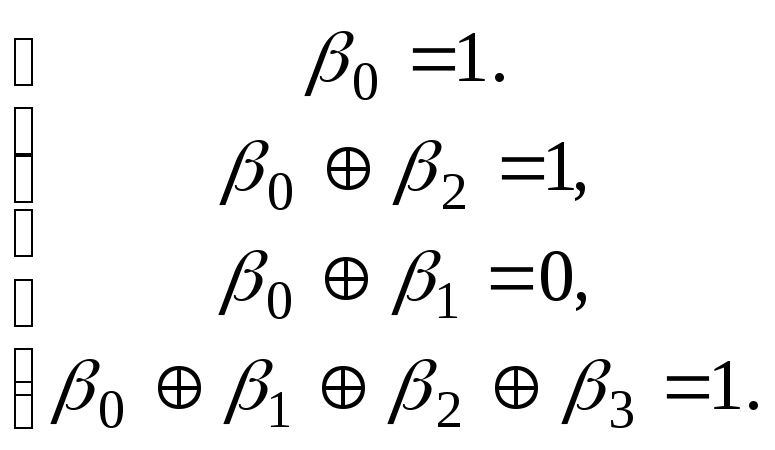 Из
системы уравнений находим
Из
системы уравнений находим
![]() .
Следовательно,
.
Следовательно,
![]()
2. (Метод преобразования формул). Имеем
![]()
(11)
Для
функций
![]() и
и
![]() функция
функция
![]() называется суперпозицией.
Класс
булевых функций
называется суперпозицией.
Класс
булевых функций
![]() называется (функционально)
полным,
если любая функция из
называется (функционально)
полным,
если любая функция из
![]() может быть представлена в виде формулы
над
может быть представлена в виде формулы
над
![]() ,
т.е. любая функция получается из функций
класса
,
т.е. любая функция получается из функций
класса
![]() применением конечного числа операции
суперпозиций.
Замечание.
Класс
применением конечного числа операции
суперпозиций.
Замечание.
Класс
![]() может быть конечным или бесконечным.
Примеры
полных классов: а)
может быть конечным или бесконечным.
Примеры
полных классов: а)
![]() ;
б)
;
б)
![]() (любая булева функция выражается формулой
в виде конъюнкции, дизъюнкции и инверсии);
в)
(любая булева функция выражается формулой
в виде конъюнкции, дизъюнкции и инверсии);
в)
![]() любую
булеву функцию можно представить в виде
полинома Жегалкина.
Пусть
любую
булеву функцию можно представить в виде
полинома Жегалкина.
Пусть
![]() некоторый класс булевых функций.
Замыканием
некоторый класс булевых функций.
Замыканием
![]() называется множество всех булевых
функций, получающихся в виде формул над
называется множество всех булевых
функций, получающихся в виде формул над
![]() (обозначается
(обозначается
![]() ).
).
Свойства замыкания:
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
Класс
![]() называется:
называется:
– замкнутым,
если
![]() ;
;
– полным,
если
![]() (см. определение выше);
(см. определение выше);
– предполным,
если
![]() не полный, но для любой функции
не полный, но для любой функции
![]() класс
класс
![]() полный.
полный.
(12)
Введем следующие классы функций (классы Поста):
![]() ;
;
![]() ;
;
 класс
самодвойственных функций;
класс
самодвойственных функций;
![]() класс
монотонных функций (функция
класс
монотонных функций (функция
![]() называется монотонной);
называется монотонной);
![]() класс
линейных функций (
класс
линейных функций (![]() называется линейной).
Лемма.
Классы
называется линейной).
Лемма.
Классы
![]() замкнуты. Доказательство.
а) Рассмотрим функцию
замкнуты. Доказательство.
а) Рассмотрим функцию
![]() ,
где
,
где
![]() .
Покажем, что
.
Покажем, что
![]() .
Действительно,
.
Действительно,
![]() Следовательно,
класс
Следовательно,
класс
![]() замкнут. б) Аналогично предыдущему
доказывается замкнутость класса
замкнут. б) Аналогично предыдущему
доказывается замкнутость класса
![]() .
в) Пусть
.
в) Пусть
![]() ,
где
,
где
![]() самодвойственные функции. Тогда
самодвойственные функции. Тогда
![]() ,
т. е. .
,
т. е. .
![]() .
Следовательно, класс
.
Следовательно, класс
![]() замкнут. г)
Пусть
замкнут. г)
Пусть
![]() ,
где
,
где
![]() .
Покажем, что
.
Покажем, что
![]() .
Пусть
.
Пусть
![]()
![]()
![]() Наборы переменных состоят из переменных,
встречающихся у функций
Наборы переменных состоят из переменных,
встречающихся у функций
![]()
![]() соответственно. Возьмем два набора
соответственно. Возьмем два набора
![]() и
и
![]() значений переменных
значений переменных
![]() .
Они определяют наборы
.
Они определяют наборы
![]() значений переменных
значений переменных
![]() причем
причем
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
.
Тогда
![]() .
Функция
.
Функция
![]() ,
поэтому
,
поэтому
![]() .
Отсюда
.
Отсюда
![]() Следовательно,
класс
Следовательно,
класс
![]() замкнут. д) Класс
замкнут. д) Класс
![]() замкнут, так как линейное выражение,
составленное из линейных выражений,
является линейным.
замкнут, так как линейное выражение,
составленное из линейных выражений,
является линейным.
(13)
Лемма
(о
несамодвойственной функции). Если
![]() ,
то из нее путем подстановки функций
,
то из нее путем подстановки функций
![]() и
и
![]() вместо
вместо
![]() можно
получить несамодвойственную функцию
одного переменного, т.е. константу.
Доказательство.
Так как
можно
получить несамодвойственную функцию
одного переменного, т.е. константу.
Доказательство.
Так как
![]() ,
то существует набор
,
то существует набор
![]() такой, что
такой, что
![]() .
.
Рассмотрим
функцию
![]() .
Пусть
.
Пусть
![]() .
Тогда
.
Тогда

Следовательно,
![]() константа
0 или 1.
константа
0 или 1.
Замечание.
Если
![]() ,
то вместо
,
то вместо
![]() подставляем
подставляем
![]() ,
если же
,
если же
![]() то
то
![]() .
Замечание.
Для того чтобы определить, является ли
функция
.
Замечание.
Для того чтобы определить, является ли
функция
![]() ,
заданная своим вектором значений
,
заданная своим вектором значений
![]() ,
самодвойственной, следует проверить,
получается ли вторая половина вектора
,
самодвойственной, следует проверить,
получается ли вторая половина вектора
![]() из
первой отражением и последующим
инвертированием его координат.
из
первой отражением и последующим
инвертированием его координат.
Лемма
(о немонотонной
функции). Если
![]() ,
то подстановкой констант
,
то подстановкой констант
![]() ,
,
![]() и функции
и функции
![]() из нее можно получить
из нее можно получить
![]() .
Доказательство.
Если
.
Доказательство.
Если
![]() ,
то найдутся два набора значений переменных
,
то найдутся два набора значений переменных
![]() и
и
![]() такие, что
такие, что
![]() и
и
![]() .
Поскольку наборы
.
Поскольку наборы
![]() и
и
![]() различаются в
различаются в
![]() координатах (
координатах (![]() ),
то, меняя по одной координате, между
ними можно вставить
),
то, меняя по одной координате, между
ними можно вставить
![]() соседних наборов, т.е. таких, что
соседних наборов, т.е. таких, что
![]()
и
каждый следующий набор получается из
предыдущего изменением ровно одной
координаты. Так как
![]() ,
то в этой цепочке найдутся два соседних
набора переменных
,
то в этой цепочке найдутся два соседних
набора переменных
![]() и
и
![]() такие, что
такие, что
![]() и
и
![]() .
Пусть эти наборы различаются в
.
Пусть эти наборы различаются в
![]() -
ой координате:
-
ой координате:
![]()
![]() .
.
Рассмотрим функцию
![]() .
.
Имеем
![]()
Поскольку,
![]() ,
то
,
то
![]() .
Замечание.
Для проверки на монотонность функции
.
Замечание.
Для проверки на монотонность функции
![]() ,
заданной своим вектором значений
,
заданной своим вектором значений
![]() ,
нужно сначала разделить его две равные
части
,
нужно сначала разделить его две равные
части
![]() и
и
![]() .
Если соотношение
.
Если соотношение
![]() не выполнено, то
не выполнено, то
![]() немонотонная. В противном случае разделим
каждый из полученных векторов опять
пополам
немонотонная. В противном случае разделим
каждый из полученных векторов опять
пополам
![]() и
и
![]() .
Проверим сначала первую пару на выполнение
соотношения
.
Проверим сначала первую пару на выполнение
соотношения
![]() ,
и в случае положительного результата
вторую. Если хотя бы для одной пары
соотношение не выполняется, то функция
немонотонная. В противном случае этот
алгоритм продолжаем дальше.
,
и в случае положительного результата
вторую. Если хотя бы для одной пары
соотношение не выполняется, то функция
немонотонная. В противном случае этот
алгоритм продолжаем дальше.
(14)
Лемма
(о нелинейной
функции). Если
![]() ,
то из нее путем подстановки констант
,
то из нее путем подстановки констант
![]() ,
,
![]() и функций
и функций
![]() и
и
![]() ,
а также, быть может, инвертированием
,
а также, быть может, инвертированием
![]() ,
можно получить функцию
,
можно получить функцию
![]() .
Доказательство.
Возьмем
полином Жегалкина для
.
Доказательство.
Возьмем
полином Жегалкина для
![]() :
:
![]() .
.
В
силу нелинейности полинома в нем найдется
член, содержащий не менее двух множителей.
Без ограничения общности можно считать,
что среди этих множителей присутствуют
![]() и
и
![]() .
Тогда можно преобразовать полином
следующим образом:
.
Тогда можно преобразовать полином
следующим образом:
![]()
![]() где
в силу единственности полинома
где
в силу единственности полинома
![]() .
.
Пусть
![]() таковы, что
таковы, что
![]() .
Тогда
.
Тогда
![]() где
где
![]() – константы, равные
– константы, равные
![]() или
или
![]() .
Рассмотрим функцию
.
Рассмотрим функцию
![]() ,
получаемую из
,
получаемую из
![]() следующим образом:
следующим образом:
![]() .
.
Очевидно, что
![]()
![]() .
.
Следовательно,
![]() .
.
(15)
Теорема
Поста (о
полноте). Для того чтобы система функций
![]() была полной необходимо и достаточно,
чтобы она целиком не содержалась ни в
одном из пяти замкнутых классов
была полной необходимо и достаточно,
чтобы она целиком не содержалась ни в
одном из пяти замкнутых классов
![]() .
Доказательство.
Необходимость.
Пусть система
.
Доказательство.
Необходимость.
Пусть система
![]() полна. Тогда
полна. Тогда
![]() .
Допустим, что
.
Допустим, что
![]() содержится целиком в каком-либо из
классов Поста (обозначим его через
содержится целиком в каком-либо из
классов Поста (обозначим его через
![]() ),
т.е.
),
т.е.
![]() .
В этом случае
.
В этом случае
![]() .
Отсюда
.
Отсюда
![]() ,
что невозможно. Достаточность.
Пусть
,
что невозможно. Достаточность.
Пусть
![]() не содержится целиком ни в одном из пяти
классов Поста. Выделим из нее подсистему
функций.
не содержится целиком ни в одном из пяти
классов Поста. Выделим из нее подсистему
функций.
![]() ,
где
,
где
![]()
![]() ,
и на ее основе построим полную систему.
,
и на ее основе построим полную систему.
1.
При помощи
![]() построим функции (константы) 0 и 1 или
функцию
построим функции (константы) 0 и 1 или
функцию
![]() .
Разберем отдельно два случая:
.
Разберем отдельно два случая:
(а)
![]() ;(б)
;(б)
![]() .
.
(а)
Рассмотрим функцию
![]() .
Из цепочки равенств
.
Из цепочки равенств
![]() следует, что
следует, что
![]() .
.
(б)
В этом случае для функции
![]() получаем
получаем
![]() ,
т.е.
,
т.е.
![]() .
Аналогичным образом, используя функцию
.
Аналогичным образом, используя функцию
![]() ,
строим константу 0 или функцию
,
строим константу 0 или функцию
![]() .
Итак, нами построены либо функция
.
Итак, нами построены либо функция
![]() ,
либо обе константы 0 и 1. или 2. Если
построена
,
либо обе константы 0 и 1. или 2. Если
построена
![]() ,
то с помощью
,
то с помощью
![]() и
и
![]() ,
применяя лемму о несамодвойственной
функции, строим константы 0 и 1. Если есть
обе константы 0 и 1, то .с помощью функций
0, 1 и
,
применяя лемму о несамодвойственной
функции, строим константы 0 и 1. Если есть
обе константы 0 и 1, то .с помощью функций
0, 1 и
![]() ,
используя лемму о немонотонной функции,
можно построить
,
используя лемму о немонотонной функции,
можно построить
![]() .
.
3.
При помощи 0, 1,
![]() и
и
![]() ,
применяя лемму о нелинейной функции,
строим функцию
,
применяя лемму о нелинейной функции,
строим функцию
![]() .
Система
.
Система
![]() полная.
Значит, и
полная.
Значит, и
![]() полная. Отсюда следует полнота системы
полная. Отсюда следует полнота системы
![]() .
Теорема доказана. Следствие
1. Из всякой
полной системы можно выделить полную
подсистему, содержащую не более пяти
функций.
.
Теорема доказана. Следствие
1. Из всякой
полной системы можно выделить полную
подсистему, содержащую не более пяти
функций.
(16)
К
а) б)
Рис. 1.7
![]() ,
то любую булеву функцию можно выразить
формулой через функции полной системы
и реализовать ее с помощью соответствующих
ФЭ. Логическая схема
,
то любую булеву функцию можно выразить
формулой через функции полной системы
и реализовать ее с помощью соответствующих
ФЭ. Логическая схема
![]() ,
выходные сигналы
,
выходные сигналы
![]() которой описываются системой булевых
функций
которой описываются системой булевых
функций
![]() ,
где
,
где
![]() входные сигналы логической схемы (
входные сигналы логической схемы (![]() ,
,
![]() ),
называется схемой из
функциональных элементов
(СФЭ).
),
называется схемой из
функциональных элементов
(СФЭ).
Теорема. Для того, чтобы для произвольной системы
 существовала
схема
существовала
схема
![]() из ФЭ с
из ФЭ с
![]() входами
входами
![]() и
и
![]() выходами
выходами
![]() необходимо и достаточно, чтобы набор
ФЭ соответствовал полной системе
функций.
необходимо и достаточно, чтобы набор
ФЭ соответствовал полной системе
функций.
Обычно
для построения схем используются базис
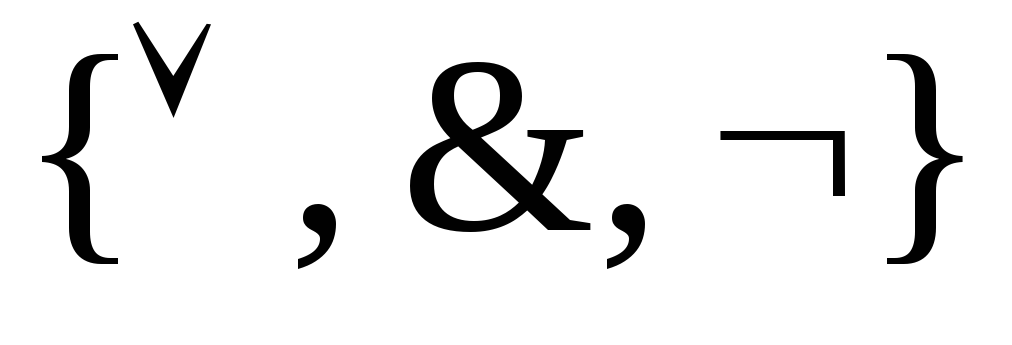 (этот базис называется стандартным
или булевым)
или
(этот базис называется стандартным
или булевым)
или
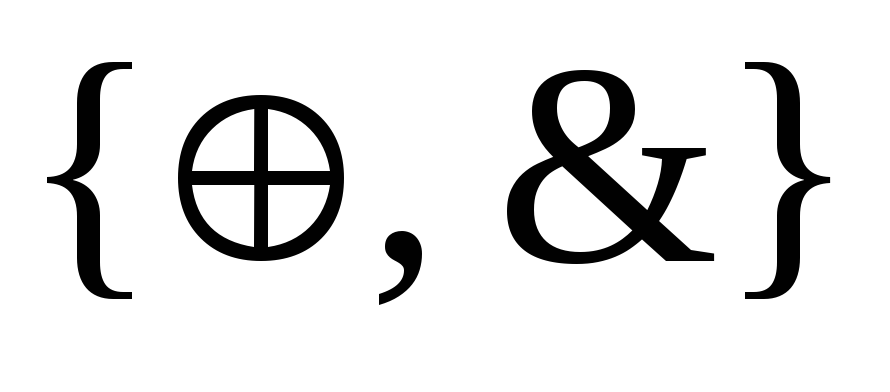 (базис
Жегалкина).
Обозначим через
(базис
Жегалкина).
Обозначим через
![]() функционал, равный числу элементов в
схеме
функционал, равный числу элементов в
схеме
![]() ,
означающий сложность
схемы.
,
означающий сложность
схемы.
Проблема синтеза – построить схему с минимальной сложностью.
