1. Назначение метода прямоугольников

Метод предназначен для приближенного численного решения интегралов. Он используется при решении не берущихся интегралов от достаточно сложных функций.

Метод считается одним из самых простых, но и наименее точным из методов численного решения. Хотя, результаты, получаемые с его помощью, приемлемы для некоторых типов расчетов. В частном случае, когда кривая на участке интегрирования представляет собой горизонтальную прямую (y=const) данным способом можно получить абсолютно точный результат.

Метод основан на разделении отрезка, на котором определен интеграл на более мелкие части и суммировании площадей прямоугольников построенных на их основе.

2. Идея метода прямоугольников

Численное значение определенного интеграла равно площади поверхности, ограниченной осью Х, отрезком подынтегральной функции и перпендикулярами из начальной и конечной точек отрезка на осьХ.

При решении интеграла мы используем правила математики, согласно которым нужно найти первообразную подынтегральной функции. Далеко, не всегда это легко, а объяснить компьютеру как найти первообразную, еще сложнее, поэтому используют численные методы, которые на основе относительно несложных расчетов, позволяют получить приблизительное значение интеграла.

Графическое представление метода прямоугольников для функции 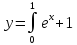на интервале от 0 до 1 приведено на рис. 2.

Приближенно, площадь под отрезком рассматриваемой функции равна сумме площадей прямоугольников S₁–S₄. Из рисунка 2 видно, что чем меньше шаг, с которым строятся прямоугольники, тем точнее вычисления.

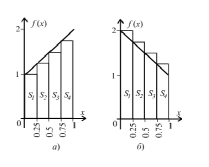
Рис. 2. Метод прямоугольников. а) Метод левых прямоугольников, б) Метод левых прямоугольников, для нисходящей функции.

В зависимости от свойств интегрируемой функции можно применять метод левых или правых прямоугольников. Отличие этих методов состоит в том, с какой стороны на интервале интегрирования начинают строить прямоугольники. На рис. 2.а показан метод левых прямоугольников. Большие стороны каждого прямоугольника рассчитываются, двигаясь слева направо, относительно точек x₁=0,x₂=0.25,x₃=0.5,x₄=0.75.

Если применять метод левых прямоугольников к нисходящим функциям, то поученные результаты, будут превышать реальное значение интеграла, как показано на рис. 2.б.

При малом шаге построений, т.е. при большом количестве прямоугольников и тот, и другой метод приводят к результатам с близкой погрешностью.

Площадь каждого прямоугольника равна произведению значения функции на шаг построения прямоугольников

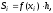
где 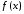- подынтегральное выражение;x_i– значение аргумента, которое рассчитывается по формуле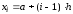(на рисунке аргументы имеют следующие значения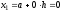,,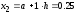,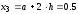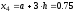);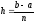– шаг, равный отношению длины отрезка (b –a), на котором производится интегрирование к числу разбиенийn.

Следовательно, итерационная формула расчета интегралов методом прямоугольников имеет вид

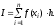
Общий ход расчета интеграла методом прямоугольников описывается следующим алгоритмом, на примере расчета выражения

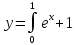
1. Выбираем число разбиений n= 4.

2. Определяем шаг изменения аргумента

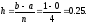
3. Рассчитываем площадь первого прямоугольника

.

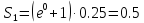4. Рассчитываем площадь второго прямоугольника

.

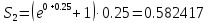5. Рассчитываем площадь третьего прямоугольника

.

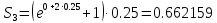6. Рассчитываем площадь четвертого прямоугольника.

.

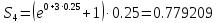7. Общая площадь прямоугольников составляет

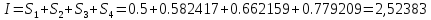
Этот результат значительно отличается от точного (1.5), что указывает на недостатки метода прямоугольников и недостаточное количество принятых разбиений. Если увеличить количество разбиений n, то точность результата возрастет. Например, приn=40 рассчитанное значение интеграла составитI=1.4875, а приn=4000I=1.4999

Большое количество разбиений позволяет получать результаты достаточно близкие к точным, поэтому расчет интегралов методом прямоугольников лучше вести с помощью компьютерной программы.