
Учебный практикум по ЭМММ
.pdf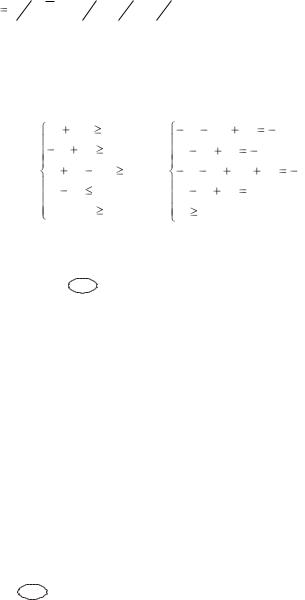
Отсутствие в столбце свободных членов отрицательных элементов свидетельствует о том, что получено оптимальное решение
L min 214 , X min( 12;0;19 4 ;0; 25 4 ;11) .
Замечание. Если решение ЗЛП и недопустимо и неоптимально, то сначала получаем допустимое решение, используя алгоритм двойственного симплекс-метода, а затем по правилам обычного симплекс-метода получаем оптимальное решение.
Пример.
L = 5x1 – x2 – x3 → max
|
x2 |
2x3 |
9, |
|
|
x2 |
|
2x3 |
x4 |
|
9, |
|
|
||||
|
|
x1 |
x2 |
1, |
|
|
x1 |
x2 |
x5 |
|
|
1, |
|
|
|
||
|
x1 |
x2 |
3x3 |
8, или |
x1 |
|
x2 |
3x3 |
x6 |
8, |
|
||||||
|
x1 |
x3 |
4, |
|
|
|
x1 |
x3 |
x7 |
4, |
|
|
|
||||
|
x1 , x2 , x3 |
0. |
|
|
x j |
0. |
|
|
|
|
|
|
|
||||
Составляем исходную симплекс-таблицу |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Баз. |
x1 |
|
x2 |
|
|
x3 |
|
x4 |
|
x5 |
|
|
x6 |
|
x7 |
Св. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
0 |
|
-1 |
|
|
-2 |
|
1 |
|
|
0 |
|
|
0 |
|
0 |
-9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x5 |
1 |
|
-1 |
|
|
0 |
|
0 |
|
|
1 |
|
|
0 |
|
0 |
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x6 |
-1 |
|
-1 |
|
|
3 |
|
0 |
|
|
0 |
|
|
1 |
|
0 |
-8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x7 |
1 |
|
0 |
|
|
-1 |
|
0 |
|
|
0 |
|
|
0 |
|
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
-5 |
|
1 |
|
|
4 |
|
0 |
|
|
0 |
|
|
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение недопустимо, так как в столбце свободных членов есть отрицательные элементы и неоптимально, так как в строке L есть отрицательная оценка (-5). Получаем сначала допустимое решение, используя алгоритм двойственного симплекс-метода. После пересчета получаем следующую симплексную таблицу
Баз. |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
Св. |
|
|
|
|
|
|
|
|
|
x2 |
0 |
1 |
2 |
-1 |
0 |
0 |
0 |
9 |
|
|
|
|
|
|
|
|
|
x5 |
1 |
0 |
2 |
-1 |
1 |
0 |
0 |
8 |
|
|
|
|
|
|
|
|
|
x6 |
-1 |
0 |
5 |
-1 |
0 |
1 |
0 |
1 |
x7 |
-1 |
0 |
-1 |
0 |
0 |
0 |
1 |
4 |
|
|
|
|
|
|
|
|
|
L |
-5 |
0 |
2 |
1 |
0 |
0 |
0 |
-9 |
|
|
|
|
|
|
|
|
|
51

В столбце свободных членов нет отрицательных элементов, но в строке L есть отрицательная оценка (-5), значит решение допустимо, неоптимально.
Используем обычный симплекс-метод и получаем следующие таблицы
Баз. |
|
x1 |
|
|
x2 |
|
x3 |
x4 |
|
x5 |
|
x6 |
|
x7 |
|
|
Св. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
0 |
|
1 |
|
2 |
-1 |
|
0 |
|
0 |
|
|
0 |
|
9 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х5 |
|
0 |
|
0 |
|
3 |
-1 |
|
1 |
|
0 |
|
|
-1 |
|
4 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х6 |
|
0 |
|
0 |
|
4 |
-1 |
|
0 |
|
1 |
|
|
1 |
|
5 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
1 |
|
0 |
|
-1 |
0 |
|
0 |
|
0 |
|
|
1 |
|
4 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
0 |
|
0 |
|
-3 |
1 |
|
0 |
|
0 |
|
|
5 |
|
11 |
|||
Баз. |
|
|
x1 |
|
|
x2 |
|
x3 |
x4 |
|
x5 |
|
x6 |
|
|
x7 |
|
|
Св. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
0 |
|
|
1 |
0 |
1 |
|
0 |
1 |
|
1 |
|
|
13 |
||||
|
|
|
2 |
|
2 |
|
2 |
|
|
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x5 |
|
1 |
|
|
0 |
0 |
1 |
|
1 |
3 |
|
7 |
|
|
1 |
||||
|
|
|
4 |
|
4 |
|
4 |
|
|
4 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x6 |
|
0 |
|
|
0 |
1 |
1 |
|
0 |
1 |
|
1 |
|
|
5 |
||||
|
|
|
4 |
|
4 |
|
4 |
|
|
4 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x1 |
|
0 |
|
|
0 |
0 |
1 |
|
0 |
1 |
|
5 |
|
|
21 |
||||
|
|
|
4 |
|
4 |
|
4 |
|
|
4 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
L |
|
0 |
|
|
0 |
0 |
1 |
|
0 |
3 |
|
23 |
|
|
59 |
||||
|
|
|
4 |
|
4 |
|
4 |
|
|
4 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсутствие в строке L отрицательных оценок свидетельствует о том, что получено оптимальное решение.
L max 59 4 , X max( 214 ;13 2 ; 5 4 ;0; 14 ;0;0) .
52

9. ДВОЙСТВЕННЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
9.1. Симметричные двойственные задачи
Каждой ЗЛП можно поставить в соответствие задачу, называемую двойственной к исходной задаче.
Рассмотрим задачу об использовании ресурсов. Предположим, что предприятие А производит n видов продукции, величина выпуска которых определяется переменными x1, x2,…,xn. В производстве используются m различных видов ресурсов, объем которых ограничен величинами b1, b2,…bn. Известны нормы затрат каждого ресурса на единицу каждого вида продукции, образующие матрицу
a11 |
a12 |
... |
a1n |
|
|
a21 |
a22 |
... |
a2n |
, |
|
... |
... ... ... |
||||
|
|||||
am1 |
am 2 |
... |
amn |
|
|
а также стоимость единицы продукции каждого вида c1, c2,…cn. Требуется организовать производство так, чтобы предприятию А была обеспечена максимальная прибыль. Задача сводится к нахождению неотрицательных переменных x1, x2,…,xn, при которых расход ресурсов не превышает заданного их количества, а стоимость всей продукции достигнет максимума. В математической форме задача записывается следующем виде:
L = c1x1 + c2x2 +…+cnxn → max |
(32) |
||||
a11x1 |
a12 x2 |
... |
a1n xn |
b1 , |
|
a 21x1 |
a 22 x2 |
... |
a 2 n xn |
b2 , |
|
при условиях .......... |
.................... |
|
.......... |
...... |
(33) |
a m1x1 |
a m 2 x2 |
... |
a mn xn |
bm , |
|
x j 0, j 1,2,..., n.
По этим же исходным данным может быть сформулирована другая задача. Предположим, что предприятие В решило закупить все ресурсы, которыми располагает предприятие А. В этом случае предприятию В необходимо установить оптимальные цены на эти ресурсы, исходя из следующих условий:
– общая стоимость ресурсов для предприятия В должна быть минимальной;
53
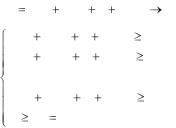
– за каждый вид ресурса предприятию А надо уплатить не менее той суммы, которую это предприятие может получить при переработке данного вида ресурса в готовую продукцию.
Если обозначить через y1, y2,…,yn цены, по которым предприятие В покупает ресурсы у предприятия А, то задача сводится к следующему: найти такие значения переменных y1, y2,…,ym, при которых стоимость ресурсов, расходуемых на единицу любого вида продукции не меньше прибыли (цены) за эту единицу продукции, а общая стоимость ресурсов достигает минимума. В математической форме задача записывается в виде:
|
|
|
|
|
|
|
|
|
L b1y1 |
b2 y2 |
... bm ym |
min, |
(34) |
||
|
a11y1 |
a21y2 ... |
am1ym |
c1 , |
|
||
|
a12 y1 |
a22 y2 ... |
am 2 ym |
c2 , |
|
||
при условии .......... |
.......... |
.......... |
.................... |
|
(35) |
||
|
a1n y1 |
a2n y2 ... |
amn ym |
cn , |
|
||
|
yi |
0,i |
1,2,..., m. |
|
|
||
Задачи (32) – (33) и (34) – (35) образуют пару взаимодвойственных задач, любая из которых может рассматриваться как исходная. Решение одной задачи дает оптимальный план производства продукции., решение другой – оптимальную систему оценок сырья, используемого для производства этой продукции.
Двойственные задачи линейного программирования называют симметричными, если они удовлетворяют следующим свойствам:
–число переменных одной задачи равно числу ограничений другой задачи;
–в одной задаче ищется максимум целевой функции, в другой – минимум;
–коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений другой задачи;
–в каждой задаче система ограничений задается в виде неравенств, причем, в задаче на отыскание максимум, все неравенства вида «≤», а в задаче на отыскание минимума, все неравенства вида «≥»;
–матрица коэффициентов системы ограничений получается одна из другой путем транспонирования;
–условия неотрицательности переменных сохраняются в обеих за-
дачах.
Пример. По исходной задаче требуется построить двойственную.
Исходная задача: L = 10x1 + 6x2 – 4x3 →min
54
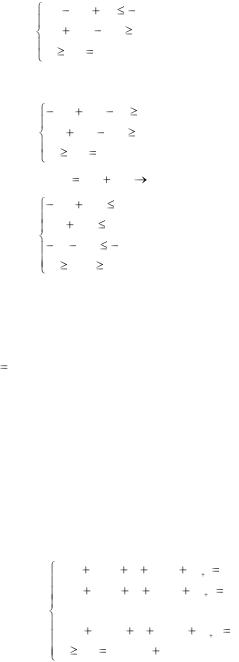
3x1 |
9x2 |
x3 |
2, |
2x1 |
2x2 |
5x3 |
3, |
x j |
0, j |
1,2,3. |
|
Приведем все неравенства системы ограничений исходной задачи к одному знаку:
3x1 |
9x2 |
x3 |
2 |
|||
2x1 |
|
2x2 |
5x3 |
3, |
||
x j |
0, j 1,2,3. |
|
||||
|
|
|
|
|
|
|
Двойственная задача. L |
|
2y1 |
3y2 |
max, |
||
3y1 |
2y2 |
10, |
|
|||
9y1 |
|
2y2 |
6, |
|
||
y1 |
|
5y2 |
4, |
|
||
y1 |
0, y2 |
0. |
|
|||
Замечание. В линейном программировании кроме симметричных двойственных пар существуют несимметричные двойственные пары. Эти задачи отличаются от симметричной пары двумя особенностями:
–ограничения задачи выражены уравнениями вместо неравенств;
–в двойственной задаче отсутствуют условия неотрицательности
переменных yi ,i 1,..., m.
9.2. Решение симметричных двойственных задач
Первая теорема двойственности. Если одна из двойственных задач имеет оптимальное решение, то оптимальное решение имеет и другая задача, при этом значения целевых функций задач равны между собой. Если целевая функция одной из задач не ограничена, то другая задача вообще не имеет решения.
Метод одновременного решения пары двойственных задач.
Двойственную пару задач (32) – (33) и (34) – (35) приведем к каноническому виду.
Исходная задача:
a11x1 |
a12 x2 |
... |
a1n xn |
xn 1 |
b1 , |
a21x1 |
a 22 x2 |
... |
a 2 n xn |
xn 2 |
b2 , |
..........................................................
am1x1 a m 2 x2 ... |
amn xn xn m bm , |
x j 0, j 1,2,..., n |
m. |
55
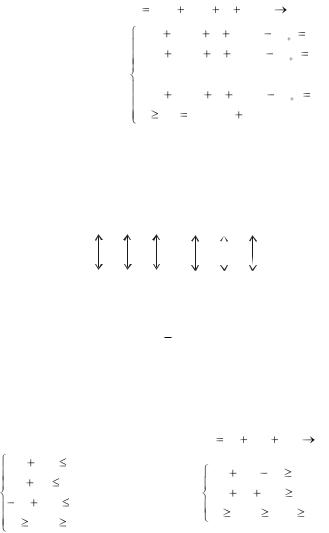
|
|
|
|
|
|
|
|
|
Двойственная задача: L b1y1 |
b2 y2 |
... |
bm ym |
min, |
||||
|
a11y1 |
a21y2 |
... |
am1ym |
ym 1 |
c1 , |
||
|
a12 y1 |
a22 y2 |
... |
am 2 ym |
ym 2 |
c2 , |
||
............................................................. |
||||||||
|
a1n y1 |
a2n y2 |
... |
amn ym |
ym n |
cn , |
||
|
yi |
0,i |
1,2,..., m n. |
|
|
|||
Число переменных в задачах одинаково и равно m + n. В исходной задаче базисными переменными являются вспомогательные неотрицательные переменные xn+1, xn+2,…,xn+m, а в двойственной задаче – вспомогательные неотрицательные переменные ym+1. ym+2,…, ym+n. Можно показать, что базисным переменным одной задачи соответствуют свободные переменные другой задачи, и наоборот, то есть:
x1 |
x2 |
xn |
xn+1 |
xn+2 |
xn+m |
ym+1 |
ym+2 |
ym+n |
y y y |
||
|
|
|
1 |
2 |
m |
Установив соответствие между переменными пары двойственных задач, и решив одну из них табличным симплексным методом, можно получить решение другой задачи. Значения базисных переменных
исходной задачи определяются L строкой оптимальной симплексной таблицы двойственной задачи, и, наоборот, значения базисных
переменных |
двойственной |
задачи определяются L |
строкой |
|||||||
оптимальной симплексной таблицы исходной задачи. |
|
|
|
|||||||
Пример 1. Найти решение пары двойственных задач. |
|
|
||||||||
Исходная задача: |
|
Двойственная задача: |
|
|||||||
|
|
|
|
|
|
|
||||
L = 4x1 + 6x2 → max |
|
L |
y1 2y2 |
3y3 |
min, |
|||||
2x1 |
5x2 |
1, |
|
2y1 |
3y2 |
y3 |
0, |
|
|
|
3x1 |
x2 |
2, |
|
|
|
|||||
|
5y1 |
y2 |
2y3 |
6, |
|
|
||||
x1 |
2x2 |
3, |
|
|
|
|||||
|
y1 |
0, y2 |
0, y3 |
0. |
|
|||||
x1 |
0, x2 |
0. |
|
|
||||||
|
|
|
|
|
|
|
|
|||
Решив исходную задачу табличным симплексным методом и учитывая соответствие между базисными и свободными переменными, получим оптимальное решение исходной и двойственной задач.
Баз. |
x1 |
x2 |
x3 |
x4 |
x5 |
Cвоб. |
|
члены |
|||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x2 |
2 |
5 |
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
x4 |
3 |
1 |
0 |
1 |
0 |
2 |
56
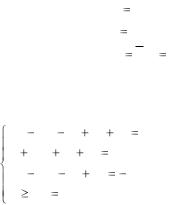
|
x5 |
-1 |
2 |
|
0 |
|
|
0 |
|
1 |
3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
-4 |
-6 |
|
0 |
|
|
0 |
|
0 |
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Баз. |
|
x1 |
|
x2 |
|
|
x3 |
|
x4 |
|
x5 |
|
Cвоб. |
||
|
|
|
|
|
|
|
|
члены |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
1 |
|
2,5 |
|
0,5 |
|
0 |
|
0 |
|
0,5 |
|||
|
x4 |
|
0 |
|
-6,5 |
|
-1,5 |
|
1 |
|
0 |
|
0,5 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x5 |
|
0 |
|
4,5 |
|
0,5 |
|
0 |
|
1 |
|
3,5 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
0 |
|
4 |
|
2 |
|
|
|
0 |
|
0 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||
|
Решение исходной задачи: |
|
Xmax |
(0,5; 0; 0; 0,5; 3,5) . |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
Решение двойственной задачи: |
|
Ymin |
(2; 0; 0; 0; 4) . |
|
|
|
|||||||||
Lmax Lmin 2.
Пример 2. Для исходной задачи составить двойственную и найти решение пары двойственных задач.
L = 3x1 – x2 + x3 + 9 → max
4x1 |
3x2 |
x3 |
x4 |
x5 6, |
x1 |
4x2 |
x3 |
x5 |
15, |
2x1 |
4x2 |
x3 |
x4 |
3, |
x j |
0, j |
1,...,5. |
|
|
Приведем данную задачу линейного программирования к виду, допускающему применение симплексного метода. Для этого, используя метод Жордана-Гаусса, приведем ЗЛП к единичному базису.
|
Баз. |
|
x1 |
|
x2 |
|
x3 |
|
x4 |
|
x5 |
|
Cвоб. |
|
|
|
|
|
|
|
члены |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
-3 |
-1 |
1 |
1 |
6 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
1 |
0 |
1 |
15 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
-4 |
-1 |
-1 |
0 |
-3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
-3 |
1 |
-1 |
0 |
0 |
9 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Баз. |
|
х1 |
|
х2 |
|
х3 |
|
х4 |
|
х5 |
|
Cвоб. |
|
|
|
|
|
|
|
члены |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х5 |
|
4 |
|
-3 |
|
-1 |
|
1 |
|
1 |
|
6 |
|
|
|
3 |
|
-7 |
|
-2 |
|
1 |
|
0 |
|
-9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
-4 |
|
-1 |
|
1 |
|
0 |
|
-3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
-3 |
|
1 |
|
-1 |
|
0 |
|
0 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
57
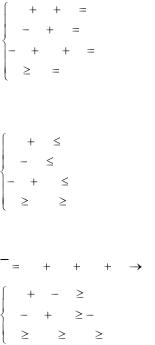
Баз. |
x1 |
x2 |
x3 |
x4 |
x5 |
Cвоб. |
|
члены |
|||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x5 |
1 |
4 |
1 |
0 |
1 |
15 |
|
|
|
|
|
|
|
|
|
x4 |
3 |
-7 |
-2 |
1 |
0 |
-9 |
|
|
|
|
|
|
|
|
|
|
-1 |
3 |
1 |
0 |
0 |
6 |
|
|
|
|
|
|
|
|
|
L |
-3 |
1 |
-1 |
0 |
0 |
9 |
|
|
|
|
|
|
|
|
|
Баз. |
x1 |
x2 |
x3 |
x4 |
x5 |
Cвоб. |
|
члены |
|||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x5 |
2 |
1 |
0 |
0 |
1 |
9 |
|
|
|
|
|
|
|
|
|
x4 |
1 |
-1 |
0 |
1 |
0 |
3 |
|
|
|
|
|
|
|
|
|
x3 |
-1 |
3 |
1 |
0 |
0 |
6 |
|
|
|
|
|
|
|
|
|
L |
-4 |
4 |
0 |
0 |
0 |
15 |
|
|
|
|
|
|
|
|
После преобразований методом Жордана-Гаусса ЗЛП можно записать в виде: L = 4x1 – 4x2 + 15 → max
2x1 x2 x5 9, x1 x2 x4 3,
x1 3x2 x3 6,
x j |
0, j 1,...,5. |
или
L = 4x1 – 4x2 + 15 → max
2x1 x2 9, x1 x2 3,
x1 3x2 6, x1 0, x2 0.
Для данной исходной задачи линейного программирования двойственная будет иметь вид:
L 9y1 3y2 6y3 15 min,
2y1 y2 y3 1,
y1 |
y2 3y3 |
2, |
y1 |
0, y2 0, y3 |
0. |
58

Установим связь между переменными прямой и двойственной задачами
х 1 |
х 2 |
х3 |
х4 |
х5 |
y 4 |
y 5 |
y1 |
y2 |
y3 |
Решим исходную задачу линейного программирования табличным симплексным методом и найдем решение обеих задач. Результирующая таблица Жордана-Гаусса совпадает с исходной симплексной таблицей,
определяющей первое допустимое решение X1 (0; 0; 6; 3; 9), L1 15.
Это решение не является оптимальным, поскольку в строке L имеется отрицательная оценка. Используя алгоритм симплексного метода, улучшим данное решение.
Баз. |
x1 |
x2 |
x3 |
x4 |
x5 |
Cвоб. |
|
члены |
|||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x5 |
2 |
1 |
0 |
0 |
1 |
9 |
|
|
|
|
|
|
|
|
|
x4 |
1 |
-1 |
0 |
1 |
0 |
3 |
|
|
|
|
|
|
|
|
|
x3 |
-1 |
3 |
1 |
0 |
0 |
6 |
|
|
|
|
|
|
|
|
|
L |
-4 |
4 |
0 |
0 |
0 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Баз. |
x1 |
x2 |
x3 |
x4 |
x5 |
Cвоб. |
|
члены |
|||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x5 |
0 |
1 |
0 |
-2 |
1 |
3 |
|
|
|
|
|
|
|
|
|
x1 |
1 |
-1 |
0 |
1 |
0 |
3 |
|
x3 |
0 |
2 |
1 |
1 |
0 |
9 |
|
|
|
|
|
|
|
|
|
L |
0 |
0 |
0 |
4 |
0 |
27 |
|
|
|
|
|
|
|
|
Результирующая симплексная таблица определяет оптимальное решение, так как в строке L нет отрицательных оценок. Итак,
Xmax (3; 0; 9; 0; 3), Lmax 27. Используя соответствие между переменными прямой и двойственной задачами, найдем решение
двойственной задачи Ymin (0; 4; 0; 0; 0), Lmin 27. Пример 3.
Для исходной задачи составить двойственную. Решить обе задачи симплексным методом или двойственным симплексным методом и по
59
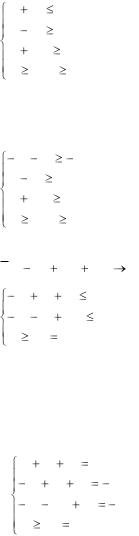
решению каждой из них найти решение другой. Одну из задач решить графическим методом.
L = x1 + x2 → min
x1 x2 8, x1 x2 4, x1 2x2 6, x1 0, x2 0.
В случае нахождения минимума целевой функции система ограничений должна иметь знак «≥». Исходная ЗЛП примет вид:
L = x1 + x2 → min
x1 |
x2 |
8, |
x1 |
x2 |
4, |
x1 |
2x2 |
6, |
x1 |
0, x2 |
0. |
Соответствующая ей двойственная задача запишется в виде:
L 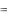 8y1 4y2 6y3 max,
8y1 4y2 6y3 max,
y1 y2 y3 1, y1 y2 2y3 1,
yi 0,i 1,2,3.
Исходную ЗЛП решим двойственным симплексным методом и графическим методом, а двойственную ЗЛП решим табличным симплексным методом и сравним решения.
Для решения исходной задачи двойственным симплексным методом
приведем ее к виду: L – x1 – x2 = 0
x1 x2 x3 8,
x1 |
x2 |
x4 |
4, |
x1 |
2x2 |
x5 |
6, |
x j |
0, j |
1,...,5. |
|
Используя алгоритм двойственного симплексного метода, найдем решение исходной ЗЛП.
60
