Учебный практикум по ЭМММ

8 6 10 4

задана матрицей 7 9 5 8 . Найдите минимальные суммарные

5 8 5 7

затраты на перевозку автомобилей.

12.22. Овощи, хранящиеся на четырех складах в количестве 50, 60, 45 и 65 т соответственно, необходимо вывезти трем магазинам. Каждый магазин должен получить овощи в количестве 100, 80 и 40 т соответственно. Со второго склада овощи не вывозятся в третий магазин, а с четвертого склада – во второй. Стоимость перевозки 1т овощей с каждого

Составьте план перевозок, обеспечивающий минимальную общую стоимость перевозок.

12.23.В резерве трех железнодорожных станций А, В, С находятся соответственно 100, 80, 120 вагонов. Составить оптимальный план перегона этих вагонов к четырем пунктам погрузки товара, если пункту 1 необходимо 90 вагонов, пункту 2 – 80 вагонов, пункту 3 – 70 вагонов

ипункту 4 – 60 вагонов. Стоимости перегонов одного вагона со станции А в указанные пункты соответственно равны 4, 5, 3, 4 д.е., со станции В – 1, 3, 5 и 1 д.е., со станции С – 6, 2, 7, 1 д.е.

12.24.В угольном бассейне добывается уголь трех сортов в относительных долях 20%, 60%, 15%. Добытый уголь доставляется четырем энергетическим установкам. Заданы теплотворные способности каждого из сортов топлива (в ккал/кг): 2800; 3000; 3500, потребности установок (в млн. ккал): 10; 25; 15; 30 и затраты по добыче 1 т. каждого сорта (в руб.): 8, 10, 15. Определить требуемый объем добычи и распределение разных сортов угля между энергетическими установками из условия минимизации суммарных затрат.

12.25.На строительном полигоне имеются два кирпичных завода, объем производства которых в сутки равен 600 и 700 т. Заводы удовлетворяют потребности пяти строительных объектов соответственно в количестве 250, 300, 150, 200 и 400 т. Кирпич на строительные объекты доставляется автотранспортом. Стоимость перевозки 1 т. кирпича с каждого из заводов соответствующим строительным полигонам указана в

7 9 3 5 4

матрице стоимостей 6 7 5 7 9 . Определить план перевозки кир-

пича строительным полигонам, обеспечивающий минимальную стоимость перевозки.

121

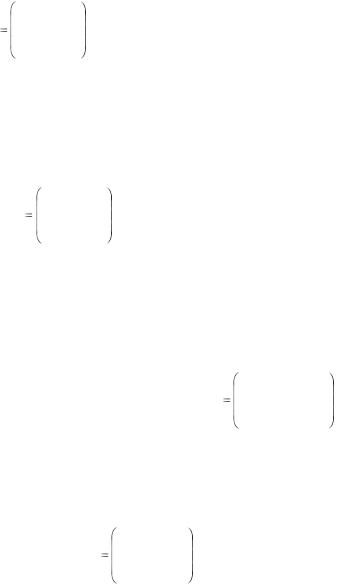
12.26. На трех складах оптовой базы сосредоточен однородный груз в количествах 90, 60 и 150 ед. Этот груз необходимо перевезти в четыре магазина. Каждый из магазинов должен получить соответственно 120, 40, 60 и 80 ед. груза. Тарифы перевозок единицы груза из каждого из складов во все магазины задаются матрицей

2 3 4 3 Ñ 5 3 1 2 .

2 1 4 2

Составить такой план перевозок, при котором общая стоимость является минимальной.

12.27. Производственное объединение имеет в своем составе три филиала, которые производят однородную продукцию соответственно в количествах, равных 50, 30 и 10 ед. Эту продукцию получают четыре потребителя, расположенные в разных местах. Их потребности соответственно равны 30, 30, 10 и 20 ед. Тарифы перевозок единицы продукции от каждого из филиалов соответствующим потребителям задаются мат-

1 2 4 1

рицей Ñ 2 3 1 5 . 3 2 4 4

Составить такой план прикрепления получателей продукции к ее поставщикам, при котором общая стоимость перевозок является минимальной.

12.28. Три предприятия данного экономического района могут производить некоторую однородную продукцию в количествах, соответственно равных 180, 350 и 20 ед. Эта продукция должна быть поставлена пяти потребителям в количествах, соответственно равных 110, 90, 120, 80 и 150 ед. Затраты, связанные с производством и доставкой

7 12 4 6 5

единицы продукции, задаются матрицей Ñ 1 8 6 5 3 . 6 13 8 7 4

Составить такой план прикрепления потребителей к поставщикам, при котором общие затраты являются минимальными.

12.29.На трех хлебокомбинатах ежедневно производится 110, 190

и90 т муки. Эта мука потребляется четырьмя хлебозаводами, ежедневные потребности которых равны соответственно 80, 60, 170 и 80 т. Тарифы перевозок 1 т муки с хлебокомбинатов к каждому из хлебозаводов

8 1 9 7

задаются матрицей Ñ 4 6 2 12 . 3 5 8 9

122

Составить такой план доставки муки, при котором общая стоимость перевозок является минимальной.

12.30.В трех хранилищах горючего ежедневно хранится 175, 125

и140 т бензина. Этот бензин ежедневно получают четыре заправочные станции в количествах, равных соответственно 180, 110, 90 и 40 т. Тарифы перевозок 1 т бензина с хранилищ к заправочным станциям зада-

9 7 5 3

ются матрицей Ñ 1 2 4 6 . 8 10 12 1

Составит такой план перевозок бензина, при котором общая стоимость перевозок является минимальной.

123

СПИСОК ЛИТЕРАТУРЫ

1.Акулич И. Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993.

2.Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем. – М.: Финансы и статистика, 2001.

3.Бережная Е.В., Бережной В.И. Экономико-математические методы и модели в примерах и задачах. – Ставрополь: Интеллект-сервис,

1996.

4.Вентцель Е.С. Исследование операций. – М.: Советское радио,

1972.

5.Кремер Н.М. Исследование операций в экономике. – М.:

ЮНИТИ, 1997.

6.Карпелевич Ф.И. Садовский Л.Е. Элементы линейной алгебры и линейного программирования. – М.: Наука, 1967.

7.Кузнецов Ю.Н. Математическое программирование. – М.: Высшая школа, 1986.

8.Калихман И.Л Сборник задач по математическому программированию. – М.: Высшая школа, 1975.

9.Таха Х. Введение в исследование операций: В 2 кн. – М.: Мир,

1985.

10.Федосеев В.В. Экономико-математические методы и прикладные модели. – М.: ЮНИТИ, 1999.

11.Руководство к решению задач с экономическим содержанием по курсу высшей математики / Под ред. А.И. Карасева и Н.Ш. Креме-

ра. – М.: ВЗФЭИ, 1989.

124

125

127