
Учебный практикум по ЭМММ
.pdf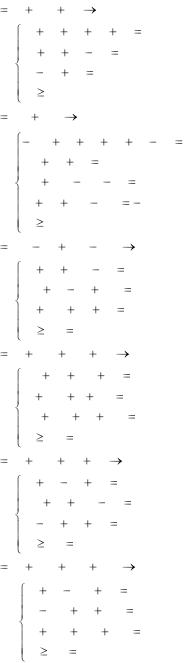
4.25. L |
x1 |
2x3 |
x5 |
min(max); |
|||||
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
5, |
||
|
|
x2 |
x3 |
x4 |
x5 |
2, |
|
||
|
|
x3 |
x4 |
x5 |
1, |
|
|
|
|
|
|
x j |
0. |
|
|
|
|
|
|
4.26. L |
3x1 |
2x2 |
|
min(max); |
|||||
|
|
2x1 x2 |
x3 |
x4 |
|
x5 x6 9, |
|||
|
|
3x1 |
x3 |
|
x5 |
3, |
|
|
|
|
|
3x1 |
2x4 |
3x5 |
x6 |
|
5, |
||
|
|
x1 |
x2 |
3x5 |
2x6 |
|
1, |
||
|
|
x j |
0. |
|
|
|
|
|
|
4.27. L |
2x1 |
x2 |
3x3 |
2x4 |
|
max; |
|||
|
|
x1 |
x2 |
2x3 |
x4 |
3, |
|||
|
|
2x1 |
x2 |
|
x3 |
2x4 |
|
4, |
|
|
|
x1 |
2x2 |
|
x3 |
x4 |
5, |
||
|
|
x j |
0, j |
|
1,...,4. |
|
|
||
4.28. L |
x1 |
2x2 |
3x3 |
x4 |
|
max; |
|||
|
|
2x1 |
x2 |
|
3x3 |
x4 |
|
6, |
|
|
|
x1 |
2x2 |
|
x3 |
2x4 |
4, |
||
|
|
3x1 |
3x2 |
x3 |
3x4 |
|
7, |
||
|
|
x j |
0, j |
|
1,...,4. |
|
|
||
4.29. L |
x1 |
2x2 |
x3 |
x4 |
|
min; |
|||
|
|
x1 |
x2 |
x3 |
x4 |
4, |
|
||
|
|
2x1 |
x2 |
|
2x3 |
x4 |
|
4, |
|
|
|
x1 |
x2 |
x3 |
x4 |
2, |
|
||
|
|
x j |
0, j |
|
1,..,4. |
|
|
|
|
4.30. L |
x1 |
2x2 |
3x3 |
4x4 |
|
min; |
|||
|
|
x1 |
x2 |
|
2x2 |
x4 |
2, |
||
|
|
x1 |
2x2 |
|
x3 |
2x4 |
|
4, |
|
|
|
x1 |
2x2 |
|
2x3 |
2x4 |
8, |
||
|
|
x j |
0, j |
|
1,...,4. |
|
|
||
91
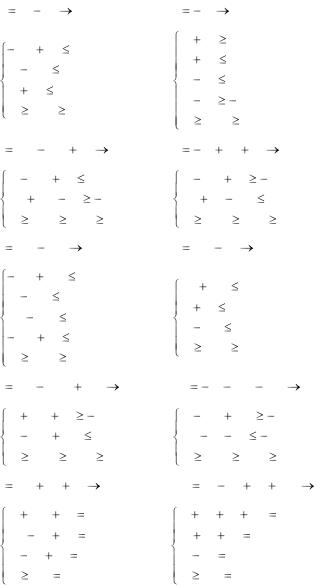
11.5. Решить задачи линейного программирования симплекс-методом
5.1. L |
x1 |
x2 |
|
max; |
|
5.2. L |
x2 |
|
min; |
|
|
|||
|
2x1 |
x2 |
|
2, |
|
x1 |
x2 |
|
1, |
|
|
|
||
|
|
|
x1 |
x2 |
|
2, |
|
|
|
|||||
|
x1 |
2x2 |
2, |
|
|
|
|
|
|
|||||
|
|
|
x1 |
x2 |
|
1, |
|
|
|
|||||
|
x1 |
x2 |
5, |
|
|
|
|
|
|
|
||||
|
|
|
|
x1 |
x2 |
|
1, |
|
|
|||||
|
x1 |
0, x2 |
|
0. |
|
|
|
|
|
|||||
|
|
|
|
x1 |
0, x2 |
|
0. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
5.3. L |
2x1 |
4x2 |
|
x3 |
min; |
5.4. L |
x1 |
x2 |
x3 |
max; |
||||
|
x1 |
2x2 |
x3 |
4, |
|
x1 |
3x2 |
|
x3 |
4, |
|
|||
|
2x1 |
3x2 |
|
x3 |
2, |
2x1 |
x2 |
|
2x3 |
1, |
|
|||
|
x1 |
0, x2 |
|
0, x3 |
0. |
x1 |
0, x2 |
|
0, x3 |
0. |
|
|||
5.5. L |
2x1 |
3x2 |
|
min; |
5.6. L 2x1 |
x2 |
min; |
|
||||||
|
5x1 |
3x2 |
15, |
|
3x1 |
2x2 |
|
11, |
|
|
||||
|
x1 |
2x2 |
4, |
|
|
|
|
|
||||||
|
|
|
x1 |
x2 |
|
2, |
|
|
|
|||||
|
5x1 |
4x2 |
|
40, |
|
|
|
|
|
|||||
|
|
|
x1 |
3x2 |
|
0, |
|
|
||||||
|
2x1 |
x2 |
|
0, |
|
|
|
|
||||||
|
|
|
x1 |
0, x2 |
|
0. |
|
|
||||||
|
x1 |
0, x2 |
|
0. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
5.7. L |
3x1 |
12x2 |
4x3 |
min; 5.8. L |
x1 |
|
2x2 3x3 |
min; |
||||||
|
x1 |
3x2 |
x3 |
2, |
x1 |
2x2 |
|
3x3 |
1, |
|
||||
|
x1 |
4x2 |
4x3 |
1, |
|
2x1 |
x2 |
|
x3 |
1, |
|
|||
|
x1 |
0, x2 |
|
0, x3 |
0. |
x1 |
0, x2 |
|
0, x3 |
0. |
|
|||
5.9. L |
2x1 |
x2 |
|
x3 |
min; |
5.10. L |
x1 |
|
x2 |
x3 |
2x4 |
max; |
||
|
x1 |
2x2 |
x3 |
1, |
|
x1 |
x2 |
x3 |
2x4 7, |
|
||||
|
2x1 |
x2 |
x4 |
2, |
|
x2 |
x3 |
x4 |
5, |
|
|
|||
|
x1 |
x2 |
x5 |
|
1, |
|
x3 |
x4 |
|
3, |
|
|
|
|
|
xi |
0 (i |
1,...,5). |
|
xi |
0 (i |
|
1,...,4). |
|
|||||
92
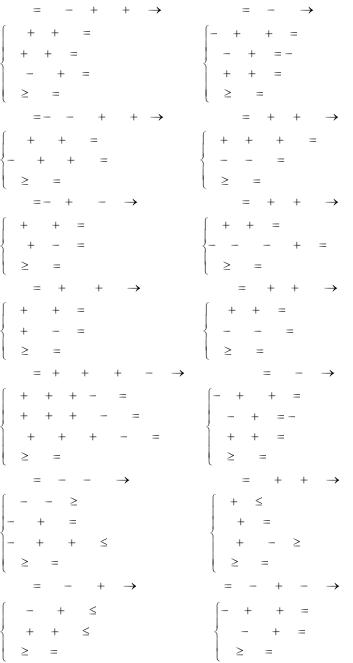
5.11. L 2x1 x2 3x3 x4 max; 5.12. L x1 2x2 max;
2x1 |
x2 |
3x3 |
10, |
|
|
x1 |
2x2 |
|
x3 |
1, |
|
|||||
x1 |
x3 |
x4 |
7, |
|
|
|
x1 |
x2 |
|
x4 |
1, |
|
||||
3x1 |
2x3 |
x5 |
4, |
|
|
x1 |
x2 |
|
x5 |
1, |
|
|
||||
xi |
0 (i |
1,...,5). |
|
|
|
xi |
0 (i |
|
1,...,5). |
|
||||||
5.13. L |
|
x1 |
2x2 |
3x4 |
4 |
max; 5.14. L |
|
x1 |
x2 |
5x3 |
max; |
|||||
2x1 |
3x2 |
2x3 |
|
2, |
|
|
x1 |
x2 |
|
4x3 |
2x4 2, |
|||||
2x1 |
3x2 |
4x3 |
1, |
|
|
x1 |
x2 |
|
2x3 |
0, |
|
|
||||
xi |
0 (i |
1,...,3). |
|
|
|
xi |
0 (i |
|
1,...,3). |
|
|
|||||
5.15. L |
|
x1 |
4x2 |
x3 |
max; |
5.16. L |
|
x1 |
x2 |
2x3 |
max; |
|||||
x1 |
2x2 |
x3 |
|
3, |
|
|
|
x1 |
x3 |
|
x4 |
4, |
|
|
||
2x1 |
x2 |
x3 |
|
0, |
|
|
|
x1 |
2x2 |
3x3 |
x4 |
0, |
||||
xi |
0 (i |
1,...,3). |
|
|
|
xi |
0 (i |
|
1,...,4). |
|
||||||
5.17. L |
|
x1 |
10x2 |
8x3 |
max; |
5.18. L |
2x1 |
x2 |
2x3 |
min; |
||||||
x1 |
4x2 |
x3 |
|
2, |
|
|
|
1x1 |
x2 |
|
x3 |
2, |
|
|
||
x1 |
2x2 |
x3 |
|
0, |
|
|
|
x1 |
3x2 |
|
2x3 1, |
|
||||
xi |
0 (i |
1,...,3). |
|
|
|
xi |
0 (i |
|
1,...,3). |
|
||||||
5.19. L |
x1 |
2x2 |
2x3 3x4 |
x5 |
max; 5.20. L |
|
2x1 |
x2 |
max; |
|||||||
x1 |
x2 |
|
x3 |
x4 2x5 |
5, |
|
x1 |
2x2 |
x3 |
1, |
|
|||||
x1 |
x2 |
|
x3 |
3x4 |
4x5 |
10, |
x1 |
x2 |
|
x4 |
1, |
|
||||
2x1 |
3x2 |
2x3 |
|
3x4 |
2x5 |
15, |
x1 |
x2 |
|
x5 |
2, |
|
|
|||
xi |
0 (i |
1,...,5). |
|
|
|
xi |
0 (i |
1,...,5). |
|
|||||||
5.21. L |
|
x1 |
x2 |
2x3 |
min; |
|
5.22. L |
|
2x1 |
x2 |
x3 |
min; |
||||
x1 |
x2 |
|
x3 |
1, |
|
|
|
x1 |
x3 |
|
4, |
|
|
|||
2x1 |
3x2 |
1, |
|
|
|
|
2x1 |
x2 |
|
4, |
|
|
||||
3x1 |
4x2 |
2x3 |
1, |
|
|
3x1 |
2x2 |
x3 |
2, |
|
||||||
x j |
0, j |
1,2,3. |
|
|
|
x j |
0, j |
1,2,3. |
|
|
||||||
5.23. L |
|
4x1 |
2x2 |
x3 |
min; |
5.24. L |
x1 |
|
x2 |
x3 |
x4 |
max; |
||||
3x1 |
2x2 |
4x3 |
|
6, |
|
|
|
x1 |
|
2x2 |
x3 |
2, |
|
|||
3x1 |
x2 |
3x3 |
18, |
|
|
3x1 |
2x2 |
x4 |
6, |
|
||||||
x j |
0, j |
1,2,3. |
|
|
|
x j |
0, j |
1,...,4. |
|
|||||||
93
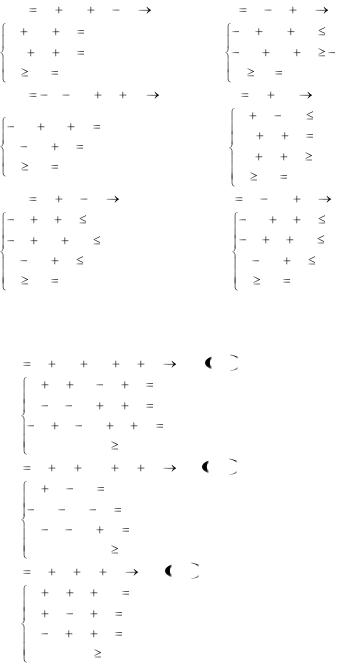
5.25. L |
x1 |
5x2 |
x3 |
x4 |
max; |
5.26. L |
x1 |
x2 |
x3 |
min; |
||
x1 |
2x2 |
x3 |
3, |
|
|
|
x1 |
2x2 |
3x3 |
3, |
||
2x1 |
x2 |
x3 |
4, |
|
|
|
2x1 |
3x2 |
x3 |
4, |
||
x j |
0, j |
1,...,4. |
|
|
|
x j |
0,1 |
1,2,3. |
|
|||
5.27. L |
x1 |
3x2 |
x3 |
x4 |
min; |
5.28. L |
x1 |
3x2 |
max; |
|||
2x1 3x |
2 x3 |
6, |
|
|
x1 |
|
x2 |
2x3 |
3, |
|||
|
|
2x1 |
x2 |
x3 |
2, |
|||||||
x1 |
3x2 |
x4 |
3, |
|
|
|
||||||
|
|
|
3x1 |
x2 |
x3 |
3, |
||||||
x j |
0, j |
1,...,4. |
|
|
|
|||||||
|
|
|
x j |
|
0, j 1,2,3. |
|||||||
5.29. L |
x1 |
x2 |
x3 |
|
max; |
|
5.30. L |
x1 |
2x2 |
x3 |
max; |
|
x1 |
x2 |
x3 |
1, |
|
|
|
|
2x1 |
x2 |
x3 |
2, |
|
x1 |
2x2 |
2x3 |
7, |
|
|
|
x1 |
x2 |
3x3 |
3, |
||
x1 |
3x2 |
x3 |
1, |
|
|
|
x1 |
3x2 |
x3 |
1, |
||
x j |
0, j |
1,2,3. |
|
|
|
x j |
0, j |
1,2,3. |
||||
11.6. Решить задачи линейного программирования |
||||||||
|
табличным симплексным методом |
|||||||
6.1. L |
x1 |
2x2 |
3x3 |
x4 |
x5 |
max min ; |
||
|
x1 |
x2 |
4x3 |
x4 |
x5 |
1, |
|
|
|
x1 |
x2 |
2x3 |
x4 |
x5 |
1, |
|
|
|
x1 |
x2 |
6x3 |
x4 x5 |
1, |
|||
|
x1 , x2 , x3 , x4 , x5 |
0. |
|
|
||||
6.2. L |
x1 |
x2 |
15x3 |
x4 |
x5 |
min max ; |
||
|
x1 |
x2 |
2x3 |
4, |
|
|
|
|
|
3x2 2x3 |
x5 |
6, |
|
|
|||
|
x1 |
x2 |
6x3 |
x4 |
12, |
|
||
|
x1 , x2 , x3 , x4 , x5 |
0. |
|
|
||||
6.3. L x1 |
x2 |
x3 |
x1 |
x2 |
x3 |
x1 |
x2 |
x3 |
x1 |
x2 |
x3 |
x1 , x2 , x3 , x4
x4 min max ; 3x4 3,
x4 1, x4 1, 0.
94
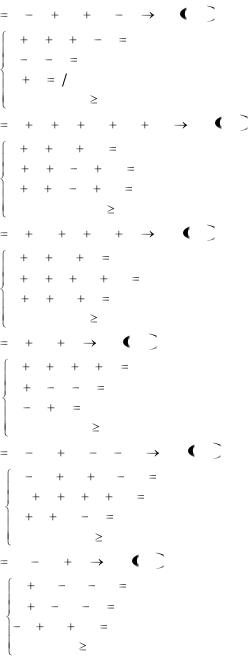
6.4. L |
x1 |
x2 |
2x3 |
3x4 |
|
x5 |
min max ; |
|||
|
x1 |
x2 |
|
x3 |
x4 |
x5 |
|
1, |
|
|
|
x1 |
x2 |
|
x4 |
2, |
|
|
|
|
|
|
x2 |
x3 |
|
1 2, |
|
|
|
|
|
|
|
x1, x2 , x3 , x4 , x5 |
0. |
|
|
|
|||||
6.5. L |
x1 |
x2 |
x3 |
|
2x4 |
3x5 |
2x6 max min ; |
|||
|
x1 |
x2 |
|
2x4 |
|
2x6 |
5, |
|
||
|
x2 |
x3 |
|
x4 |
x5 |
2x6 |
2, |
|
||
|
x1 |
x3 |
x4 |
x5 |
2x6 |
3, |
|
|||
|
x1 , x2 , x3 , x4 , x5 , x6 |
|
0. |
|
||||||
6.6. L |
x1 |
2x2 |
x3 |
3x4 |
|
x5 |
max min ; |
|||
|
x1 |
x2 |
|
2x4 |
|
x5 |
5, |
|
|
|
|
x1 |
x2 |
|
x3 |
3x4 |
2x5 9, |
||||
|
x2 |
x3 |
|
2x4 |
|
x5 |
6, |
|
|
|
|
x1 , x2 , x3 , x4 , x5 |
0. |
|
|
|
|||||
6.7. L |
x1 |
2x3 |
x5 |
min max ; |
||||||
|
x1 |
x2 |
|
x3 |
x4 |
x5 |
|
5, |
|
|
|
x2 |
x3 |
|
x4 |
x5 |
2, |
|
|
||
|
x3 |
x4 |
|
x5 |
1, |
|
|
|
|
|
|
x1 , x2 , x3 , x4 , x5 0. |
|
|
|
||||||
6.8. L |
x1 |
3x2 |
5x3 |
x4 |
|
5x5 |
max min ; |
|||
|
x1 |
2x2 |
3x3 |
3x4 |
|
5x5 |
0, |
|||
|
2x1 |
x2 |
x3 |
x4 |
5x5 |
5, |
||||
|
x1 |
x3 |
2x4 |
x5 |
|
2, |
|
|||
|
x1 , x2 , x3 , x4 , x5 |
0. |
|
|
|
|||||
6.9. L |
3x1 |
2x2 |
x4 |
|
max min ; |
|||||
|
x1 |
2x2 |
3x3 |
3x4 |
|
3, |
|
|||
|
x1 |
x2 |
2x3 |
x4 |
|
2, |
|
|||
|
x1 |
2x2 |
2x4 |
1, |
|
|
||||
|
x1 , x2 , x3 , x4 |
0. |
|
|
|
|
||||
95

6.10. L |
3x1 |
2x2 |
3x4 |
|
x5 |
max min ; |
|||
|
3x1 |
2x2 |
|
x3 |
x4 |
2, |
|
||
|
4x1 |
x2 |
|
x4 |
x5 |
|
21, |
|
|
|
4x1 |
x2 |
|
x4 |
x5 |
|
15, |
|
|
|
x1 |
x2 |
|
x6 |
|
4, |
|
|
|
|
x1 , x2 , x3 , x4 , x5 , x6 |
0. |
|
||||||
6.11. L |
x1 |
x2 |
|
2x3 |
x4 |
x5 |
max min ; |
||
|
x1 |
x2 |
|
2x3 |
3x4 |
2x5 |
3, |
||
|
x2 |
x3 |
|
x4 |
x5 |
|
0, |
|
|
|
x1 |
x4 |
|
x5 |
|
0, |
|
|
|
|
x1 , x2 , x3 , x4 , x5 |
0. |
|
||||||
6.12. L |
x1 |
x2 |
|
x3 |
5x4 |
max min ; |
|||
|
x1 |
x2 |
|
x4 |
|
3, |
|
|
|
|
x1 |
x2 |
3x4 |
1, |
|
|
|||
|
2x1 |
x2 |
|
x3 |
x4 |
|
5, |
|
|
|
x1 , x2 , x3 , x4 |
0. |
|
|
|
||||
6.13. L |
x1 |
3x2 |
|
max min ; |
|
||||
|
2x1 |
x2 |
|
x5 |
x6 |
|
10, |
|
|
|
2x1 |
2x2 |
x4 |
x6 |
25, |
|
|||
|
2x1 |
3x2 |
|
x3 |
x5 |
9, |
|
||
|
6x1 |
x3 |
|
x4 |
36, |
|
|
||
|
x1 , x2 , x3 , x4 , x5 , x6 |
0. |
|
||||||
6.14. L |
x1 |
x2 |
|
4x3 |
x4 |
x5 |
max min ; |
||
|
x1 |
x2 |
|
x3 |
x4 |
x5 4, |
|
||
|
x1 |
x2 |
|
x4 |
|
2, |
|
|
|
|
x1 |
x2 |
|
x3 |
10, |
|
|
|
|
x1 , x2 , x3 , x4 , x5 0.
96
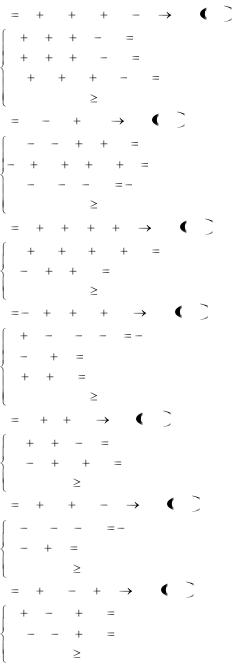
6.15. L |
x1 |
2x2 |
|
2x3 |
3x4 |
x5 |
max min ; |
|||||
x1 |
|
x2 |
|
x3 |
|
x4 |
2x5 |
5, |
|
|||
x1 |
|
x2 |
|
x3 |
|
3x4 |
4x5 |
10, |
||||
2x1 |
3x2 |
2x3 |
3x4 |
2x5 |
15, |
|||||||
x1 , x2 , x3 , x4 , x5 |
0. |
|
|
|
|
|||||||
6.16. L |
8x1 |
|
5x2 |
|
13x3 |
|
max min ; |
|||||
2x1 |
x2 |
x3 |
|
x4 |
3x5 |
6, |
|
|||||
x1 |
2x2 |
x3 |
3x4 |
x5 |
15, |
|||||||
2x1 |
4x2 |
x3 |
2x4 |
|
3, |
|
||||||
x1 , x2 , x3 , x4 , x5 |
0, |
|
|
|
|
|||||||
6.17. L |
x1 |
x2 |
x3 |
x4 |
|
x5 |
|
max min ; |
||||
2x1 |
3x2 |
5x3 |
7x4 |
9x5 |
19, |
|||||||
x1 |
|
x2 |
|
x4 |
|
2x5 |
|
2, |
|
|
|
|
x1 , x2 , x3 , x4 , x5 |
0. |
|
|
|
|
|||||||
6.18. L |
|
x1 |
|
x2 |
|
5x3 |
|
2x4 |
max min ; |
|||
x1 |
|
x2 |
|
3x3 |
|
x4 |
x5 |
|
3, |
|
||
x1 |
|
3x3 |
x4 |
|
6, |
|
|
|
|
|
||
x2 |
|
x3 |
|
2x4 |
7, |
|
|
|
|
|||
x1 , x2 , x3 , x4 , x5 |
0. |
|
|
|
|
|||||||
6.19. L |
3x2 |
|
x3 |
|
2x4 |
|
min max ; |
|||||
3x1 |
x2 |
x3 |
|
x4 |
|
5, |
|
|
|
|||
3x1 |
x2 |
2x3 |
4x4 |
|
1, |
|
|
|||||
x1 , x2 , x3 , x4 |
|
0. |
|
|
|
|
|
|||||
6.20. L |
x1 |
2x2 |
|
3x3 |
x4 |
|
max min ; |
|||||
x1 |
|
3x2 |
x3 |
|
2x4 |
|
4, |
|
|
|||
x1 |
|
x2 |
|
x3 |
|
0, |
|
|
|
|
|
|
x1 , x2 , x3 , x4 |
|
0. |
|
|
|
|
|
|||||
6.21. L |
x1 |
2x2 |
|
x3 |
x4 |
max min ; |
||||||
x1 |
|
x2 |
|
2x3 |
|
3x4 |
1, |
|
|
|||
2x1 |
x2 |
x3 |
|
3x4 |
2, |
|
|
|||||
x1 , x2 , x3 , x4 |
|
0. |
|
|
|
|
|
|||||
97
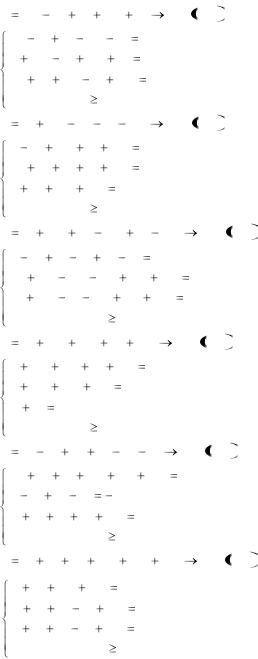
6.22. L |
2x1 x2 |
|
x3 |
|
3x4 |
x5 |
|
min max ; |
||||
2x1 |
x2 |
x3 |
3x4 |
x5 |
10, |
|
|
|||||
x1 |
2x2 |
x3 |
4x4 |
x5 |
8, |
|
|
|
||||
2x1 |
x2 |
3x3 |
|
x4 |
2x5 |
4, |
|
|
||||
x1 , x2 , x3 , x4 , x5 |
|
0. |
|
|
|
|
|
|||||
6.23. L |
x1 |
3x2 |
x3 |
|
x4 |
5x5 |
|
max min ; |
||||
x1 |
x2 |
2x3 |
x4 |
5x5 |
5, |
|
|
|
||||
2x1 |
x2 |
x3 |
x4 |
5x5 |
5, |
|
|
|
||||
x1 |
x2 |
2x3 |
6x4 |
6, |
|
|
|
|
||||
x1 , x2 , x3 , x4 , x5 |
|
0. |
|
|
|
|
|
|||||
6.24. L |
x1 |
2x2 |
|
x3 |
|
2x4 |
x5 |
|
2x6 |
max min ; |
||
x1 |
x2 |
x3 |
|
x4 |
|
x5 |
x6 |
7, |
|
|||
2x1 |
3x2 |
|
2x3 |
|
3x4 |
2x5 |
|
3x6 |
0, |
|||
3x1 |
2x2 |
|
x3 |
|
4x4 |
3x5 |
2x6 |
10, |
||||
x1 , x2 , x3 , x4 , x5 , x6 |
0. |
|
|
|
|
|||||||
6.25. L |
x1 |
2x2 |
|
2x3 |
x4 |
6x5 |
max min ; |
|||||
x1 |
3x2 |
3x3 |
|
x4 |
9x5 |
18, |
|
|||||
x1 |
5x2 |
2x4 |
8x5 |
13, |
|
|
|
|||||
x2 |
x5 |
3, |
|
|
|
|
|
|
|
|
|
|
x1 , x2 , x3 , x4 , x5 |
|
0, |
|
|
|
|
|
|||||
6.26. L |
x1 |
x2 |
x3 |
|
x4 |
x5 |
x6 |
|
max min ; |
|||
2x1 |
x2 |
x3 |
3x4 |
3x5 |
2x6 |
7, |
||||||
x1 |
x3 |
x5 |
|
x6 |
|
2, |
|
|
|
|
||
x2 |
x3 |
x4 |
|
x5 |
|
2x6 |
5, |
|
|
|
||
x1 , x2 , x3 , x4 , x5 , x6 |
0. |
|
|
|
|
|||||||
6.27. L |
x1 |
x2 |
x3 |
|
2x4 |
3x5 |
|
2x6 |
max min ; |
|||
x1 |
|
x2 |
2x4 |
2x6 |
5, |
|
|
|
|
|||
x2 |
|
x3 |
x4 |
x5 |
2x6 |
2, |
|
|
|
|||
x1 |
|
x3 |
x4 |
|
x5 |
|
2x6 |
3, |
|
|
|
|
x1 , x2 , x3 , x4 , x5 , x6 |
0. |
|
|
|
|
|||||||
98
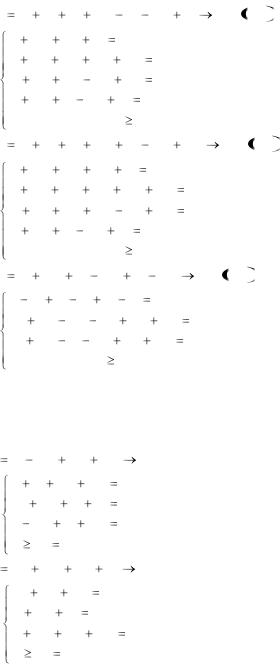
6.28. L |
x1 |
x2 |
x3 |
3x4 |
x5 |
2x6 |
x7 |
max min ; |
||
|
x1 |
2x2 |
3x6 |
|
x7 |
8, |
|
|
|
|
|
x1 |
3x2 |
2x3 |
|
2x6 |
3x7 |
15, |
|
|
|
|
x2 |
3x3 |
2x4 |
3x6 |
3x7 |
4, |
|
|
||
|
x3 |
3x4 |
x5 |
2x6 |
x7 |
5, |
|
|
||
|
x1 , x2 , x3 , x4 , x5 , x6 , x7 |
0. |
|
|
|
|||||
6.29. L |
x1 |
x2 |
x3 |
5x4 |
x5 |
2x6 |
2x7 |
max min ; |
||
|
x1 |
2x2 |
6x5 |
3x6 |
x7 |
7, |
|
|
||
|
x1 |
3x2 |
2x3 |
|
7x5 |
2x6 |
3x7 |
12, |
|
|
|
x2 |
3x3 |
2x4 |
4x5 |
3x6 |
3x7 |
8, |
|
||
|
x3 |
3x4 |
x5 |
2x6 |
x7 |
4, |
|
|
||
|
x1 , x2 , x3 , x4 , x5 , x6 , x7 |
0. |
|
|
|
|||||
6.30. L |
x1 |
2x2 |
x3 |
2x4 |
x5 |
2x6 |
max min ; |
|||
|
x1 |
x2 x3 |
x4 |
x5 |
x6 |
7, |
|
|
||
|
2x1 |
3x2 |
2x3 |
3x4 |
|
2x5 |
3x6 |
0, |
|
|
|
3x1 |
2x2 |
x3 |
|
4x4 |
3x5 |
2x6 |
7, |
|
|
|
x1 , x2 , x3 , x4 , x5 , x6 |
0. |
|
|
|
|
||||
11.7. Решить задачи линейного программирования табличным симплекс-методом и провести анализ на чувствительность
7.1. L |
x1 |
2x2 |
2x3 |
|
3x4 |
max; |
|
x1 |
x2 2x3 |
2x4 |
8, |
||
|
2x1 |
2x2 |
x3 |
|
x4 |
10, |
|
x1 |
2x2 |
x3 |
2x4 |
1, |
|
|
x j |
0, j |
1,...,4. |
|
||
7.2. L |
3x1 |
2x2 |
3x3 |
x4 |
min; |
|
|
2x1 |
3x2 |
3x4 |
10, |
|
|
|
x2 |
2x3 |
x4 |
|
4, |
|
|
x1 |
2x2 |
2x3 |
|
2x4 |
8, |
|
x j |
0, j |
1,...,4. |
|
||
99
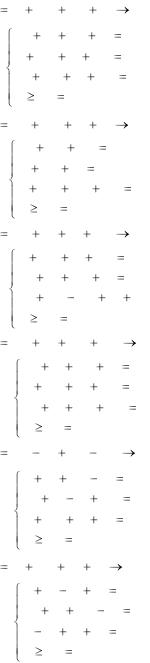
7.3. L x1 2x2
2x1 x2 x1 2x2 3x1 3x2 x j 0, j
7.4. L 3x1 2x2
2x1 2x2 x2 2x3 x1 2x2 x j 0, j
7.5. L 2x1 x2
x1 2x2 2x1 x2 2x1 2x2 x j 0, j
7.6. L 2x1 x2
2x1 x2 x1 2x2 2x1 x2 x j 0, j
3x3 x4 max;
3x3 x4 12,
x3 2x4 8, x3 3x4 15,
1,...,4.
x3 x4 min; 3x3 9,
x4 4,
2x3 2x4 8, 1,...,4.
x3 2x4 max; x3 2x4 16, 2x3 x4 14,
2x3 x4 4, 1,...,4.
2x3 2x4 min;
2x3 x4 8, x3 2x4 10,
2x3 2x4 10, 1,...,4.
7.7. L |
2x1 |
x2 |
3x3 |
2x4 |
max; |
|
x1 |
x2 |
2x3 |
x4 |
3, |
|
2x1 |
x2 |
x3 |
2x4 |
4, |
|
x1 |
2x2 |
x3 |
x4 |
5, |
|
x j |
0, j |
1,...,4. |
|
|
7.8. L |
x1 2x2 |
x3 |
x4 |
min; |
|
|
x1 |
x2 |
x3 |
x4 |
4, |
|
2x1 |
x2 |
2x3 x4 |
4, |
|
|
x1 |
x2 |
x3 |
x4 |
2, |
|
x j |
0, j |
1,...,4. |
|
|
100
