НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОАЛЬНОГО ОБРАЗОВАНИЯ

МЕЖДУНАРОДНАЯ АКАДЕМИЯ БИЗНЕСА И НОВЫХ ТЕХНОЛОГИЙ

/Академия МУБиНТ/

Кафедра_ИКТ (информационно-компьютерных технологий)

по дисциплине Теория вероятностей и математическая статистика_____

Тема Контрольная работа______________________________

	Выполнил: студент группы 1ЗБ5ПИ-21 __Брыкалова Тамара Владимировна _ (подпись, ФИО) «_10_» __ февраля __ 20_14_г.
	Преподаватель: кандидат технических наук, доцент _ (должность, ученая степень) __Черномордик Владимир Дмитриевич _ (подпись, ФИО) «______» _____________ 20____г.
	Оценка_________________

Ярославль, 2014

Две последние цифры номера зачетной книжки: 76. Согласно таблицам выбора параметров (m и n) получаю: .

Теория вероятностей Блок 1. Случайные события

Задача 1.

В ящике находятся 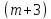одинаковых пар перчаток черного цвета и одинаковых пары перчаток бежевого цвета (все перчатки в ящике лежат поштучно). Найти вероятность того, что две наудачу извлеченные перчатки образуют пару.

Решение.

По условию задачи дано:

5 пар перчаток черного цвета – 10 штук перчаток черного цвета

3 пары перчаток бежевого цвета – 6 штук перчаток бежевого цвета

16 штук перчаток всего черного и бежевого цвета.

Событие F – две наудачу извлеченные перчатки образуют пару.

Событие F – это результат либо события A, либо события B.

Событие A – извлечена пара перчаток черного цвета.

Событие B – извлечена пара перчаток бежевого цвета.

Поскольку события A и B – несовместные, то вероятность события F находим как сумму вероятностей событий A и B.

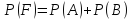
Найдем вероятность события A (две наудачу извлеченные перчатки образуют пару черного цвета):

1. Вероятность извлечь первую перчатку черного цвета вычисляем как отношение благоприятствующих случаев ( 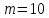черных перчаток) к общему числу перчаток ():

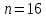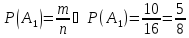
2. Вероятность извлечь вторую перчатку черного цвета, при условии, что первая перчатка черного цвета с противоположной руки вычисляем как отношение благоприятствующих случаев (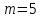) к общему количеству перчаток за вычетом одной извлеченной (:

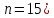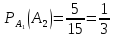
3. Тогда вероятность события A вычислим по формуле произведения вероятностей зависимых событий:

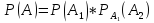
Находим вероятность события B (две наудачу извлеченные перчатки образуют пару бежевого цвета):

1. Вероятность извлечь первую перчатку бежевого цвета вычисляем как отношение благоприятствующих случаев ( 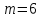перчаток бежевого цвета) к общему числу перчаток (:

2. Вероятность извлечения второй перчатки бежевого цвета с противоположной руки, при условии, что первая извлеченная перчатка была бежевого цвета с противоположной руки, вычисляем как отношение благоприятствующих случаев (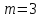) к общему числу перчаток за вычетом одной извлеченной (

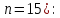
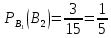
3. Тогда вероятность события B найдем по формуле произведения вероятностей зависимых событий:

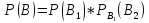
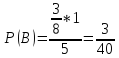
Теперь находим вероятность события F как сумму вероятностей событий A и B:

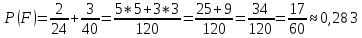
Ответ: Вероятность того, что две наудачу извлеченные перчатки образуют пару, равна .

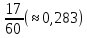Задача 2.

В урне находятся 3 шара белого цвета и 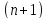шара черного цвета. Шар наудачу извлекается и возвращается в урну три раза. Найти вероятность того, что среди извлеченных шаров окажется:

а). ровно два белых шара; б) не менее двух белых шаров.

Решение.

По условию задачи дано:

Количество шаров всего .

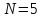Количество испытаний

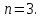
Событие A – извлечение белого шара.

Вероятность события A (извлечение белого шара) в каждом испытании одинакова и составляет

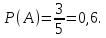
a). Поскольку вероятность извлечения белого шара в каждом испытании постоянна 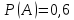и количество испытаний 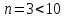, то вероятность того, что среди извлеченных шаров окажется ровно два белых шара (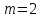) можно вычислить, применяя формулу Бернулли:

где

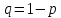
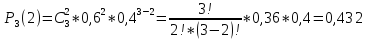
б). Вероятность того, что среди извлеченных шаров окажется не менее двух белых шаров находим, применяя снова формулу Бернулли:

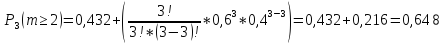
Ответ: Вероятность того, что среди извлеченных шаров окажется:

а). ровно два белых шара равна ;

б). не менее двух белых шаров равна .

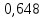Задача 3.

В урне находятся 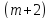белых и 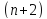черных шара. Три шара последовательно извлекаются без возвращения их в урну. Найти вероятность того, что третий по счету шар окажется белым.

Решение.

По условию задачи дано:

Количество белых шаров: .

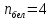Количество черных шаров: .

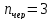Общее количество шаров: .

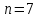Количество испытаний: 3.

Событие F – извлечение белого шара в третьем испытании.

Вероятность события F:

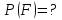
Всего возможно 4 исхода в первых двух испытаниях:

1. Событие 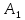: Ч-Ч (первый и второй извлеченные шары черные);

2. Событие 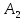: Ч-Б (первый извлеченный шар - черный, второй – белый);

3. Событие 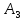: Б-Ч (первый извлеченный шар – белый, второй – черный);

4. Событие 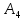: Б-Б (первый и второй извлеченные шары белые).

Событие F – третий извлеченный шар – белый.

В силу того, что события единственно возможные, а событие F может произойти только вместе с одним из событий 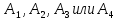, то справедливо равенство:

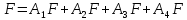
В силу того, что события 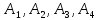несовместные, то для вычисления вероятности события F можно применить формулу сложения вероятностей несовместных событий:

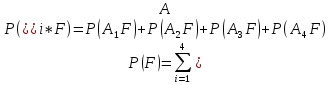
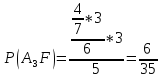
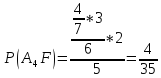
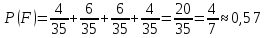
Ответ: вероятность того, что третий по счету шар окажется белым составляет