3.Гомоморфизмы и изоморфизмы.
Определение.Пусть даны группы G и G
и G .Тогда
отображение f : G
.Тогда
отображение f : G →
G
→
G называется гомоморфизмом ,если для
любых g,h
принадлежащих G
называется гомоморфизмом ,если для
любых g,h
принадлежащих G выполняется
выполняется
 .
.
Утверждение1.Если f
: G →
G
→
G -гомоморфизм
групп и
-гомоморфизм
групп и
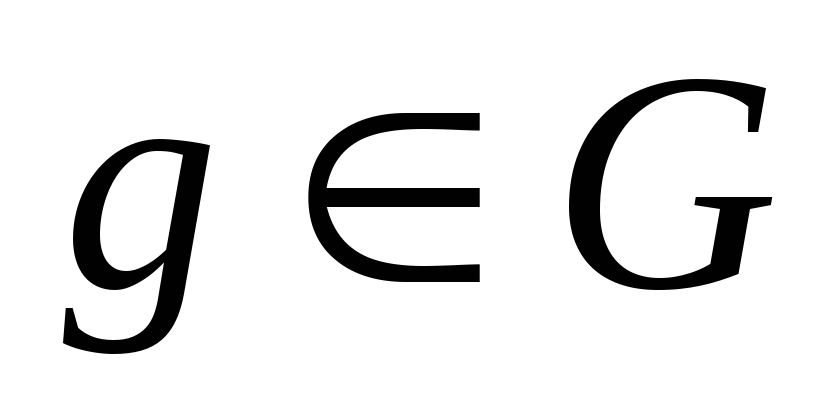 .Тогда
.Тогда
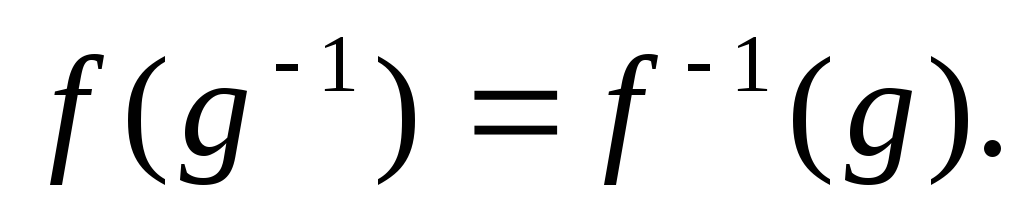
Доказательство.
Действительно,
 •
•
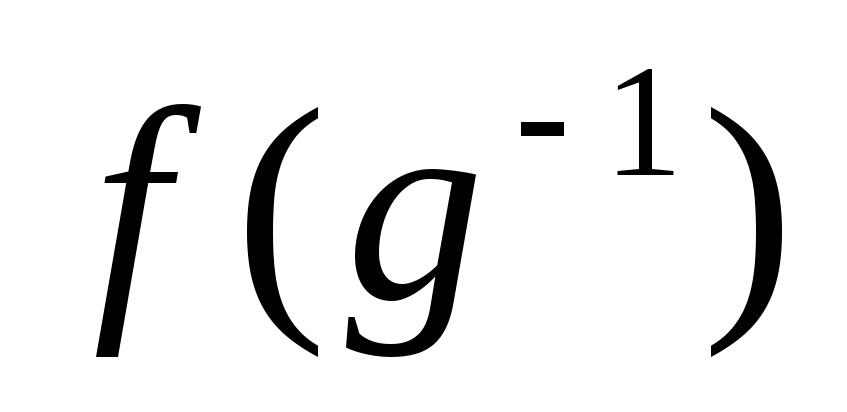 =
= •
•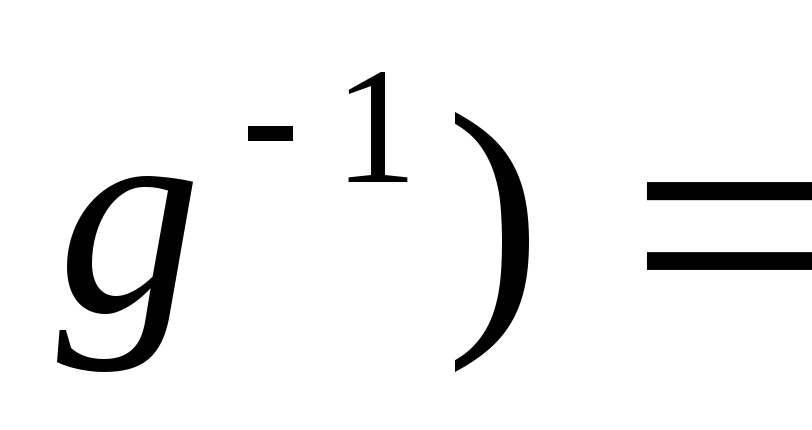
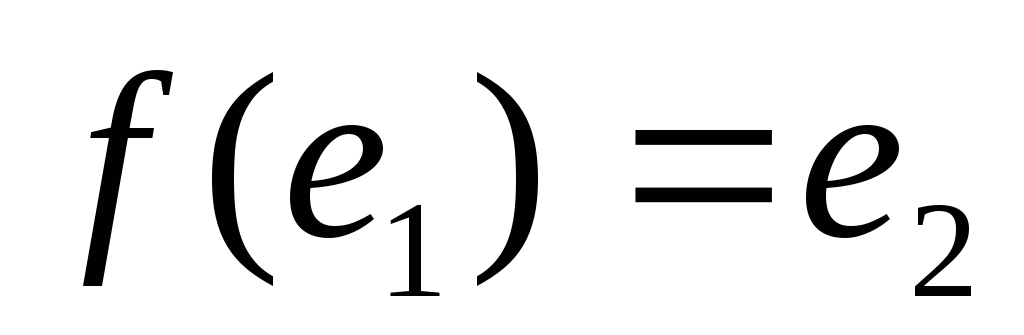 .Аналогично
.Аналогично
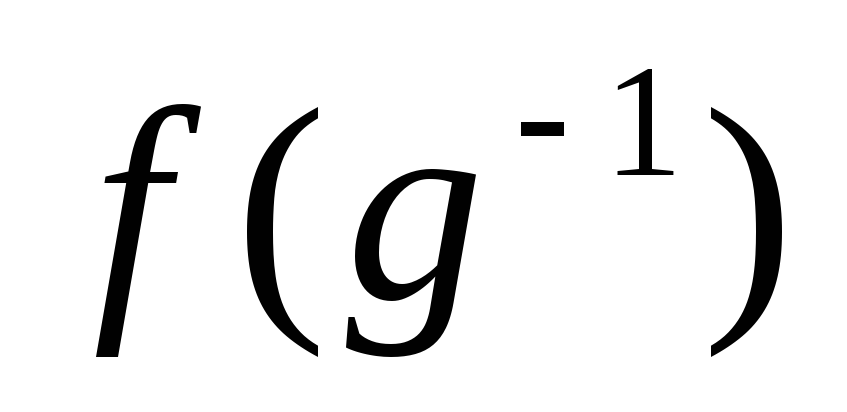 •
•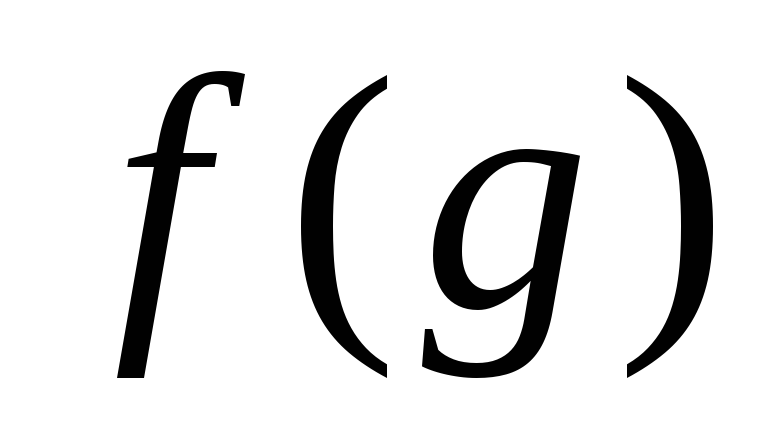 =
= .Это
означает, что
.Это
означает, что
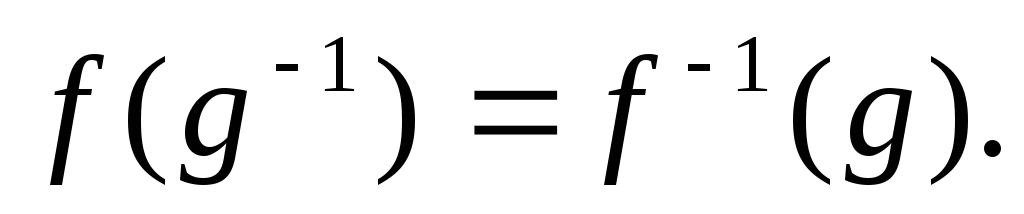 Утверждение1 доказано.
Утверждение1 доказано.
Утверждение2.Если f
: G →
G
→
G -
гомоморфизм групп,
-
гомоморфизм групп,
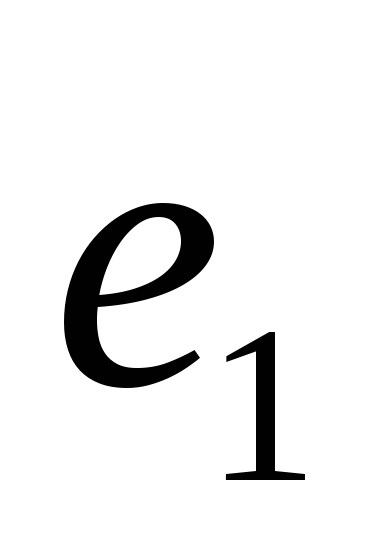 и
и
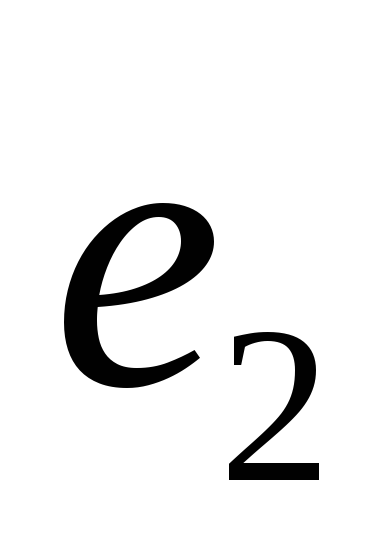 - единицы групп G
- единицы групп G ,G
,G соответственно.Тогда
соответственно.Тогда
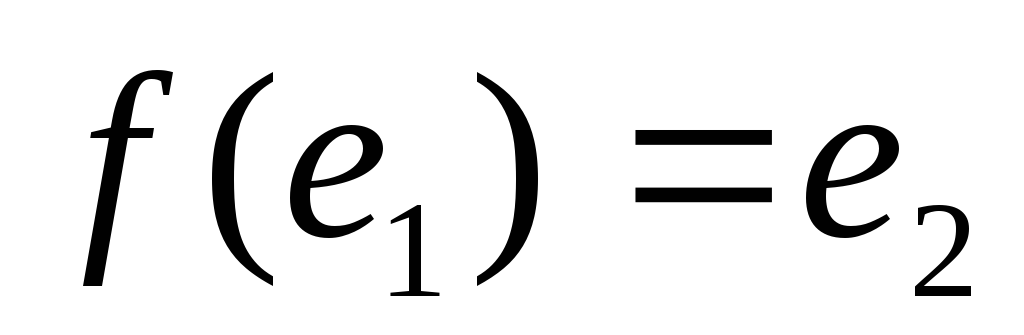 .
.
Доказательство.
Умножая левую часть и правую части
равенства
 •
•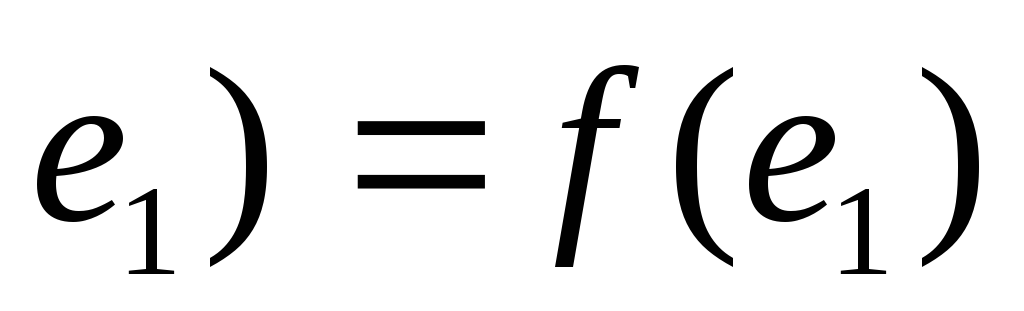 •
•
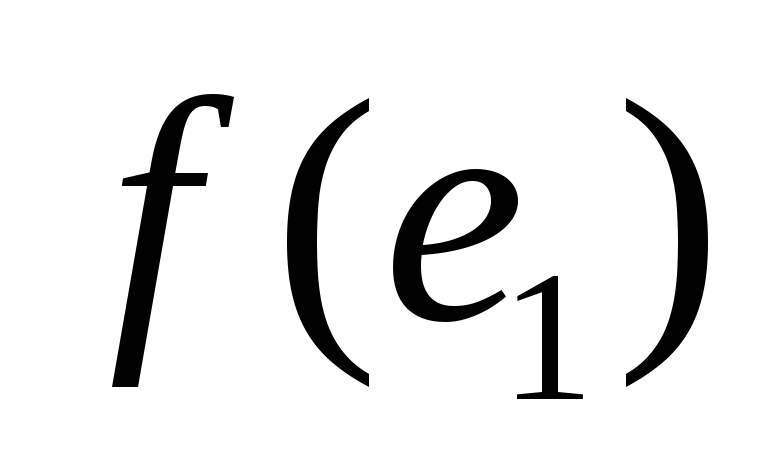 на
на
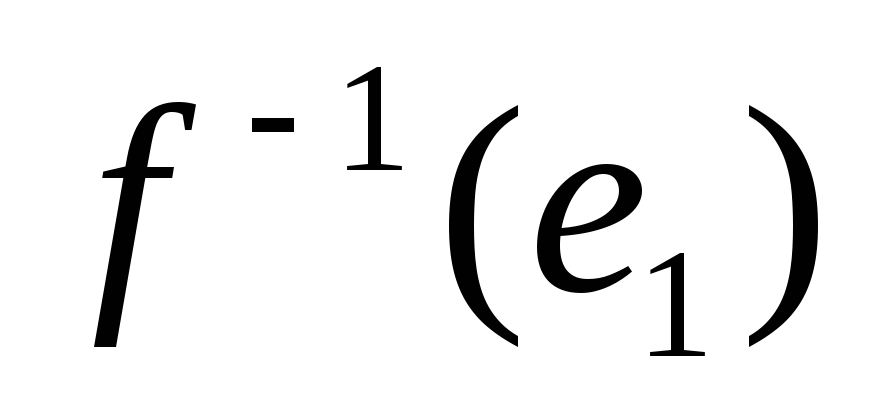 ,получим
требованное.Утверждение2 доказано.
,получим
требованное.Утверждение2 доказано.
Утверждение3.Если f
: G →
G
→
G -гомоморфизм
групп и
-гомоморфизм
групп и
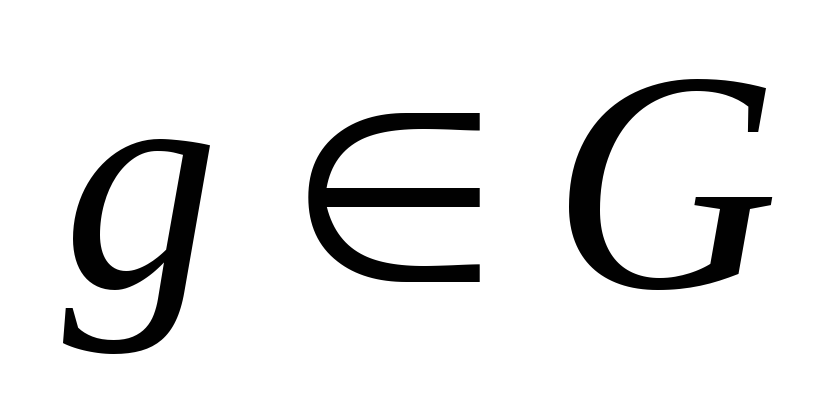 -элемент
конечного порядка.Тогда элемент
-элемент
конечного порядка.Тогда элемент
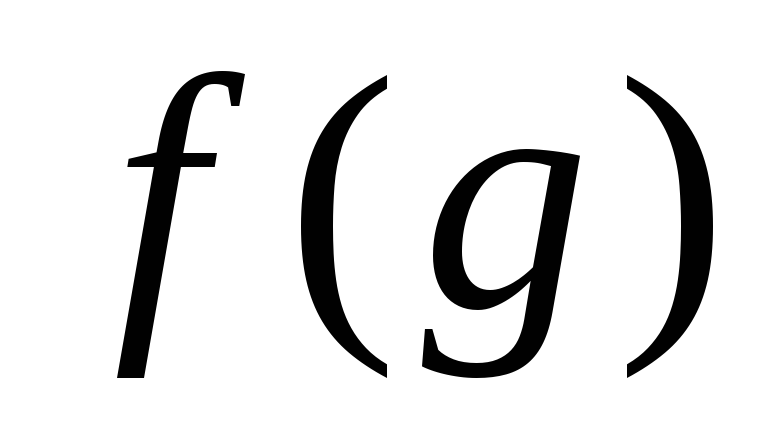 также имеет конечный порядок ,причем,
если
также имеет конечный порядок ,причем,
если
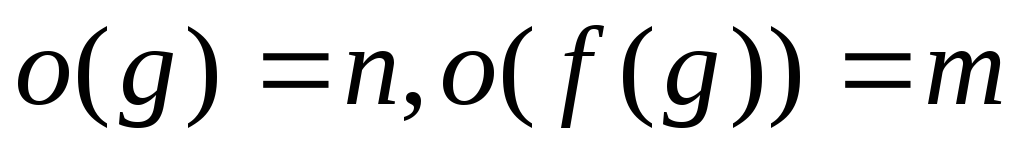 ,то
,то
 делится на
делится на
 .
.
Доказательсво.
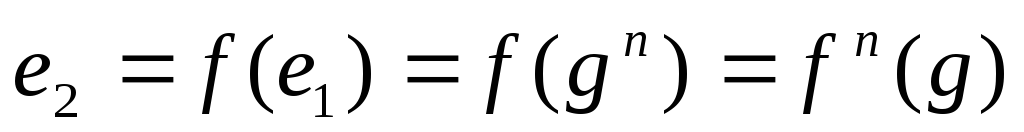 .Поэтому
элемент
.Поэтому
элемент
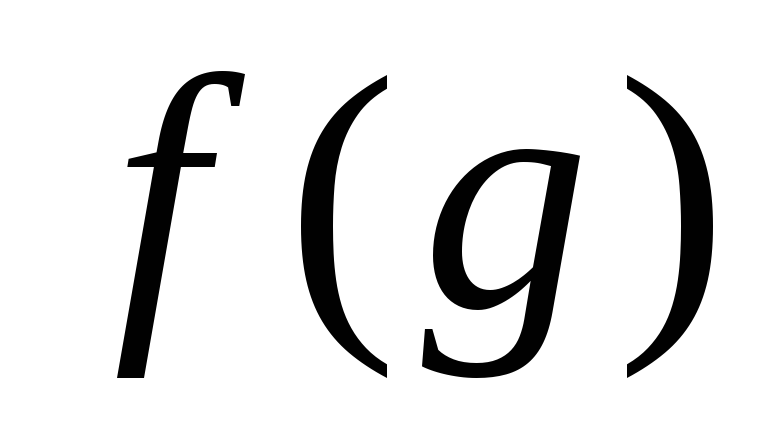 имеет конечный порядок.Допустим, что
имеет конечный порядок.Допустим, что
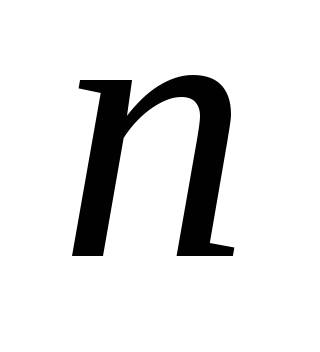 не делится на
не делится на
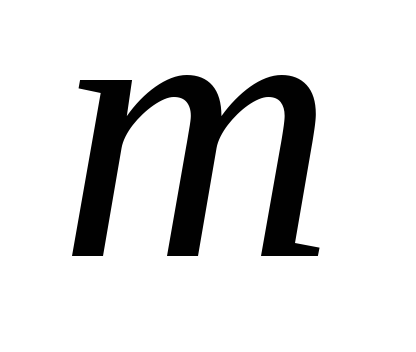 .Тогда
.Тогда
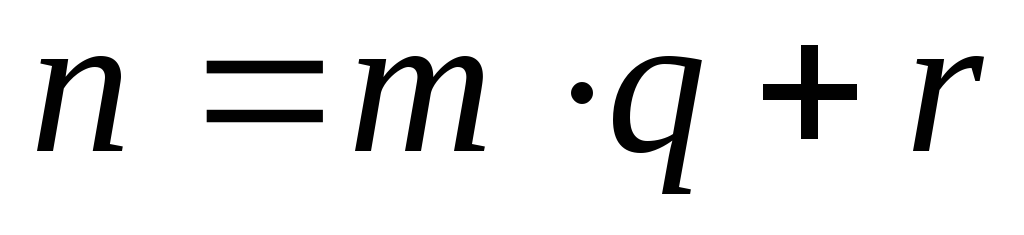 ,где
,где
 .В
этом случае получаем:
.В
этом случае получаем:
 ,что
противоречит тому ,что
,что
противоречит тому ,что
 -наименьшая
степень такая ,что
-наименьшая
степень такая ,что
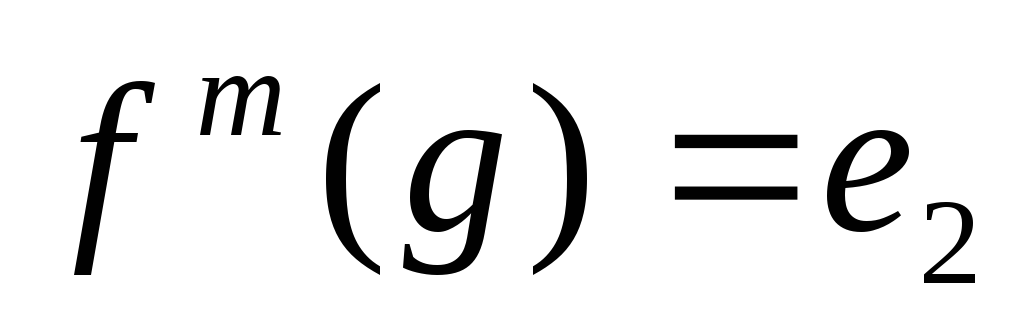 .
Утверждение3 доказано.
.
Утверждение3 доказано.
Определение.Гомоморфизм который
является взаимнооднозначным называют
изоморфизм.
Каждую конечную группу можно задать с
помощью таблицы умножения или таблицы
Кэли.В каждой строке и каждом столбце
таблицы Кэли каждый элемент группы
встречается ровно один раз.Если элементы
группы перенумеровать, то каждому
элементу будет соответствовать некоторая
перестановка.Это наблюдение приводит
к теореме.
Теорема Кэли.Любая конечная группа
из
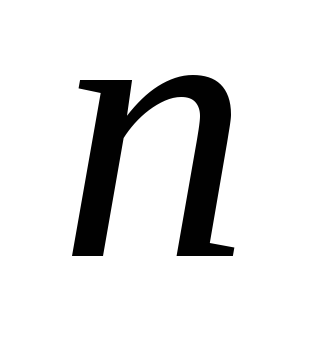 элементов изоморфна некоторой подгруппе
группы S
элементов изоморфна некоторой подгруппе
группы S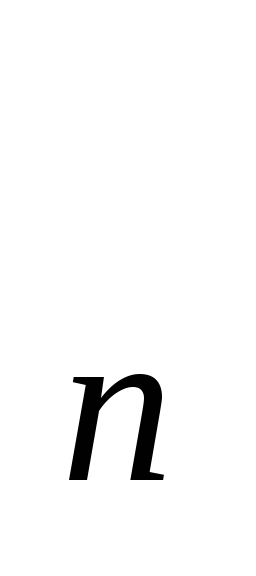 .
.
Доказательство.
Пусть G-конечная группа
из
 элементов.Переномеруем элементы группы
и рассмотрим ее таблицу Кэли.Тогда
каждую строчку можно рассматривать как
перестановку чисел
элементов.Переномеруем элементы группы
и рассмотрим ее таблицу Кэли.Тогда
каждую строчку можно рассматривать как
перестановку чисел
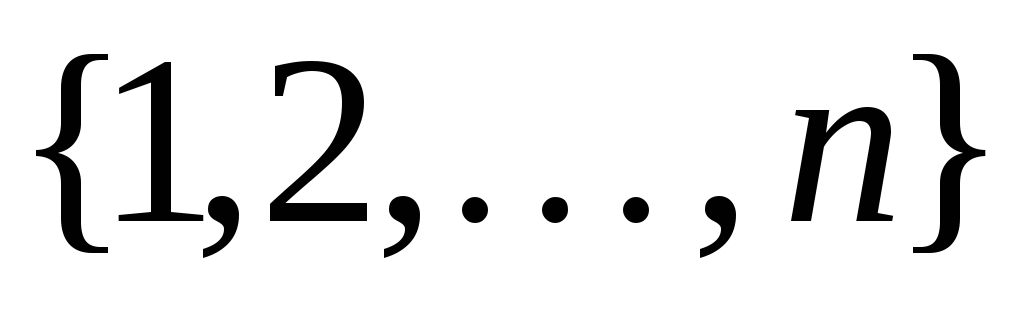 .Сопоставим
каждому элементу g строчку
таблицы Кэли,рассматриваемую как
перестановку
.Сопоставим
каждому элементу g строчку
таблицы Кэли,рассматриваемую как
перестановку
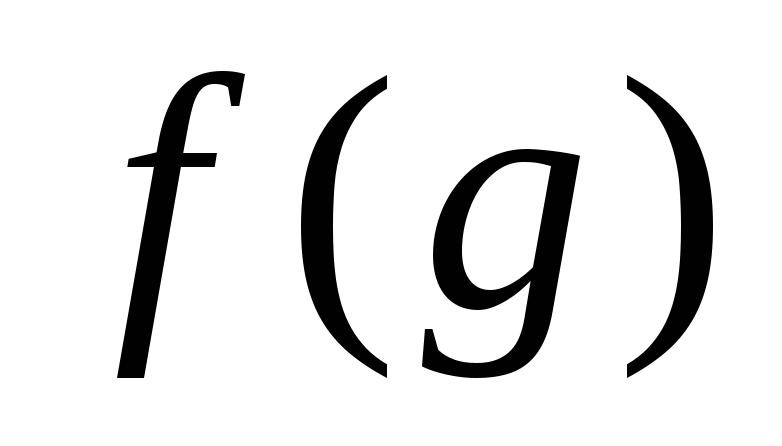 .Достаточно
убедится в том ,что
.Достаточно
убедится в том ,что
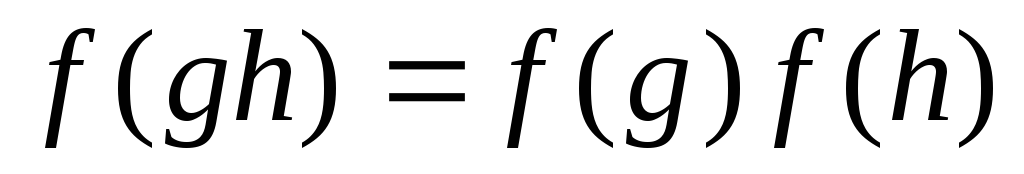 .
.
Пусть
 .Тогда перестановка
.Тогда перестановка
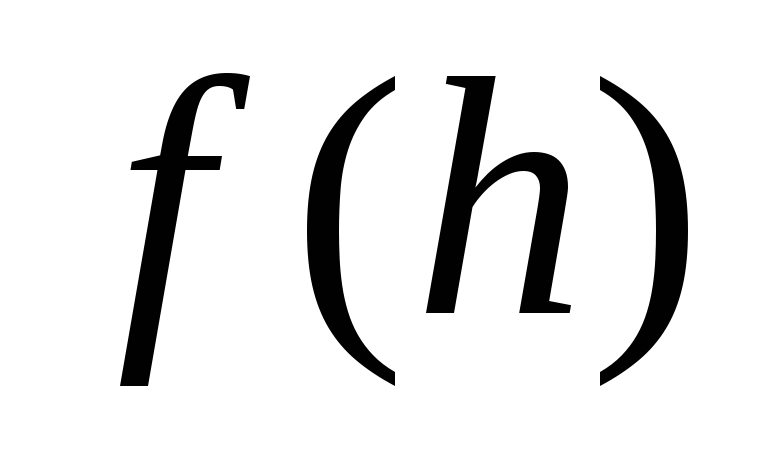 элемент
элемент
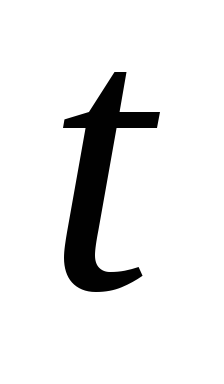 переведет в элемент
переведет в элемент
 Далее , перестановка
Далее , перестановка
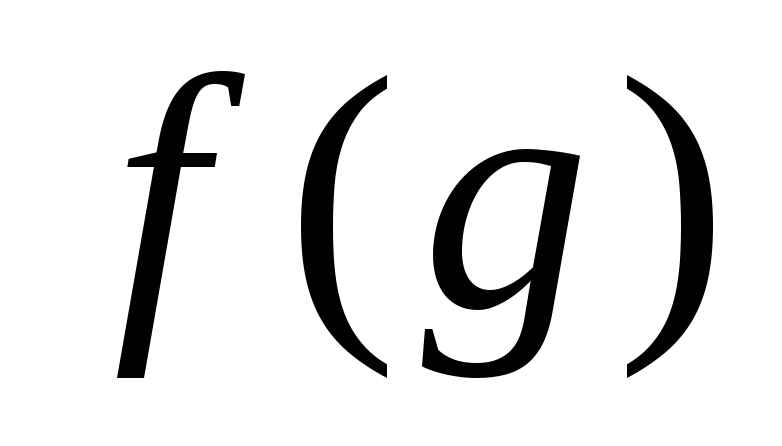 элемент
элемент
 переведет в элемент
переведет в элемент
 .Но
тоже самое с элементом
.Но
тоже самое с элементом
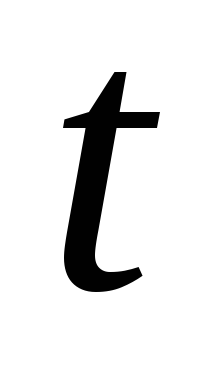 сделает перестановка
сделает перестановка
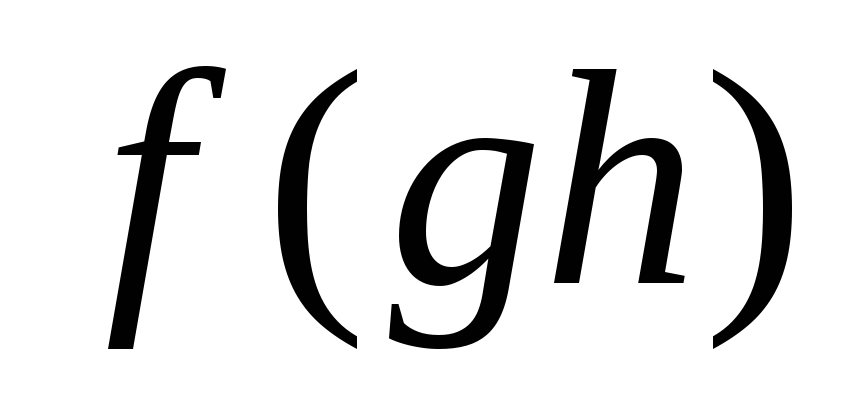 .Значит,
.Значит,
 .
.
Теорема доказана.
Например группе движений правильного
пятиугольника D изоморфна группа подстановок S
изоморфна группа подстановок S .Каждому
преобразованию группы D
.Каждому
преобразованию группы D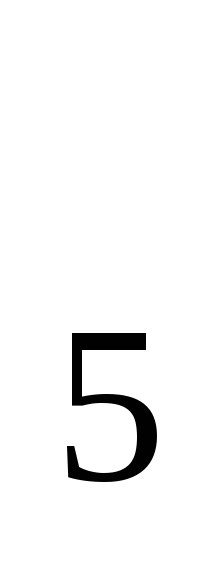 можно сопоставить перестановку-перестановку
вершин правильного пятиугольника
ABCDF.Прономеруем
вершины: A→1,
можно сопоставить перестановку-перестановку
вершин правильного пятиугольника
ABCDF.Прономеруем
вершины: A→1,
B→2,C→3,D→4,F→5.Тогда
отображение D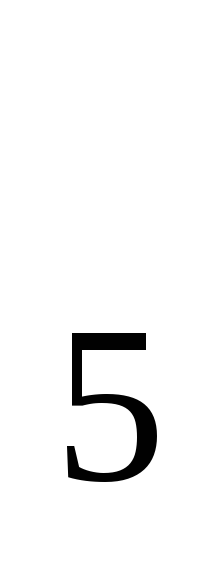 →
S
→
S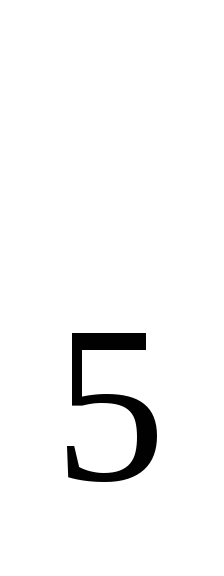 ,при
котором
,при
котором
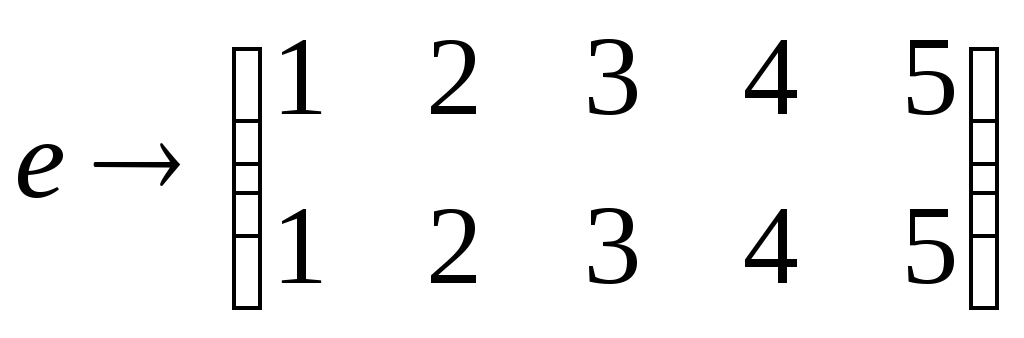 ,
,
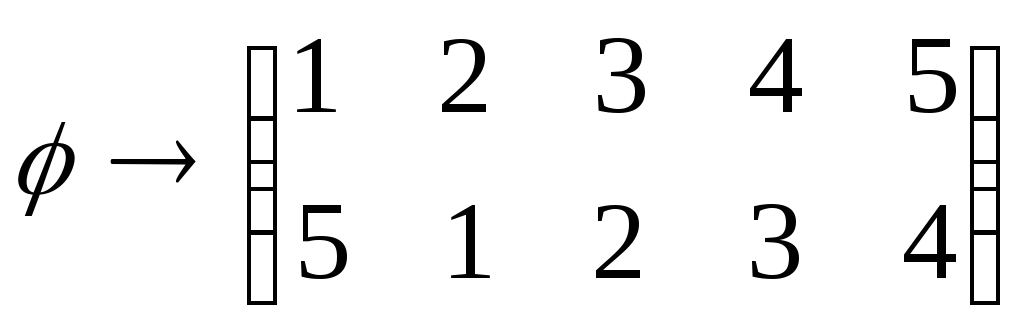 ,
,
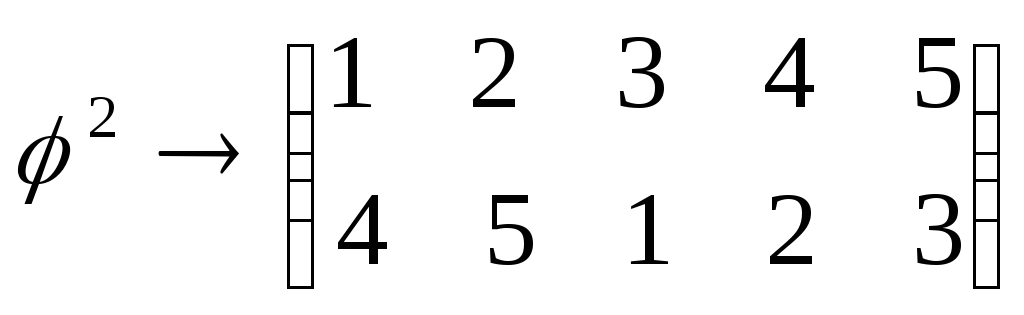 ,
,
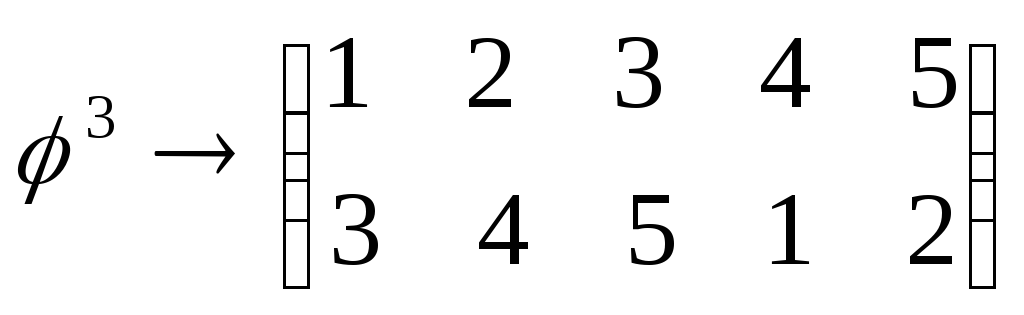 ,
,
 ,
,
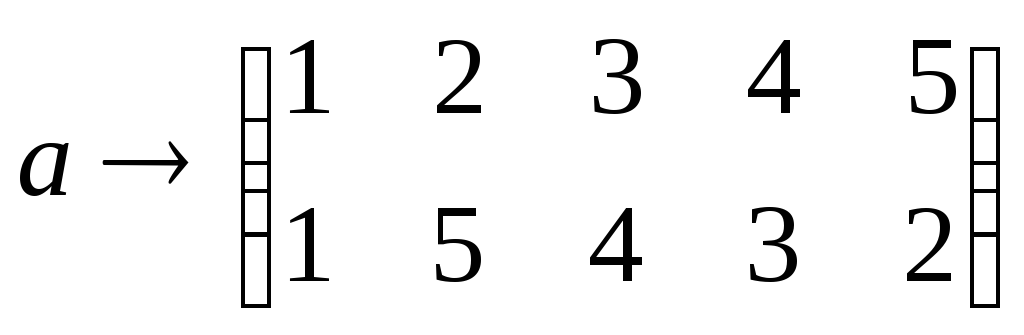 ,
,
 ,
,
 ,
,
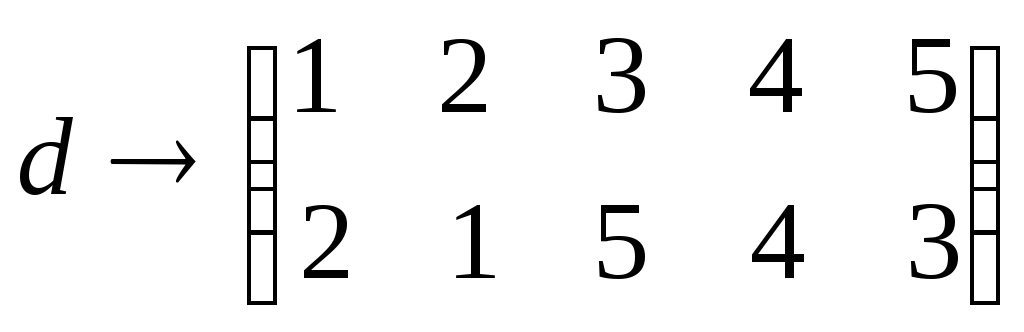 ,
,
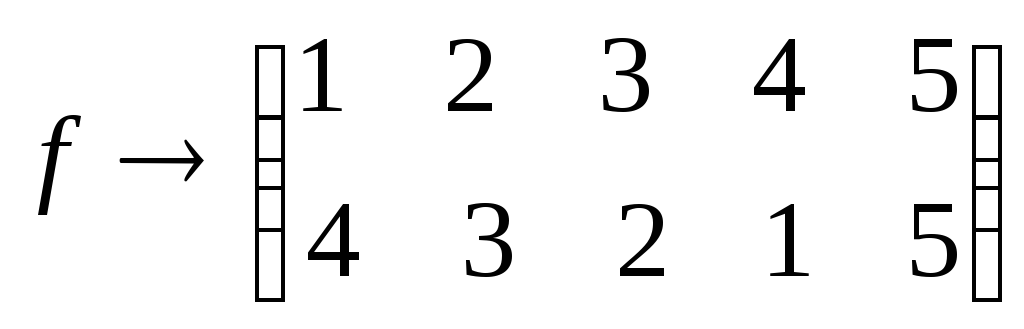 ,
,
является изоморфизмом.
Изоморфизм отображающий G
на себя называется автоморфизмом.

