Добавил:

korayakov Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

Дискретная математика

Файл:

Курсовые / 1 / Дискра курсач / Курсовик..doc

Скачиваний:

Добавлен:

16.04.2013

Размер:

357.89 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОННОЙ ТЕХНИКИ

Технический университет Курсовая работа

по теме: «Об одной группе 12 порядка»

Выполнил: студент ЭКТ-36 Петров А.Б.

Преподаватель: Клюшин А.В.

Москва 2004

Содержание

Теоретическая часть 3 стр.

1 Группы 3 стр.

2 Подгруппы 4 стр.

Практическая часть

Задание и его решение 5 стр.

Список использованной литературы 6 стр

1.Группы

Определение. Множество – это собрание определённых и различимых между собой объектов, мыслимых как единое целое.

Пусть G-некоторое множество.

Определение. Бинарной операцией на множестве G называется произвольное отображение G×G→G из декартова квадрата в само множество G.

Определение. Если ,то результат бинарной операции обозначается •,где (•)-знак бинарной операции.

Множество G с бинарной опреацией (•) называется группой если:

для любых ••=•(•;
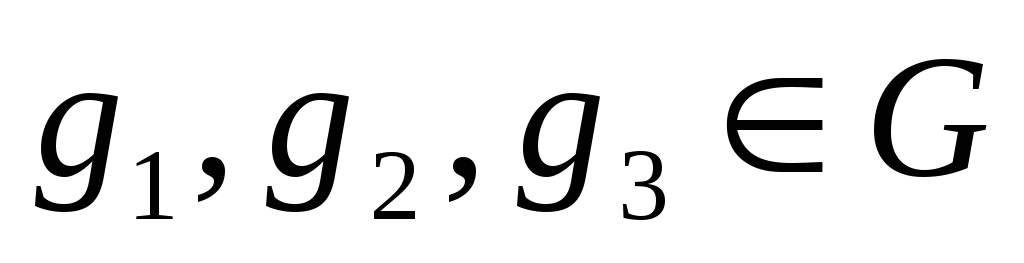
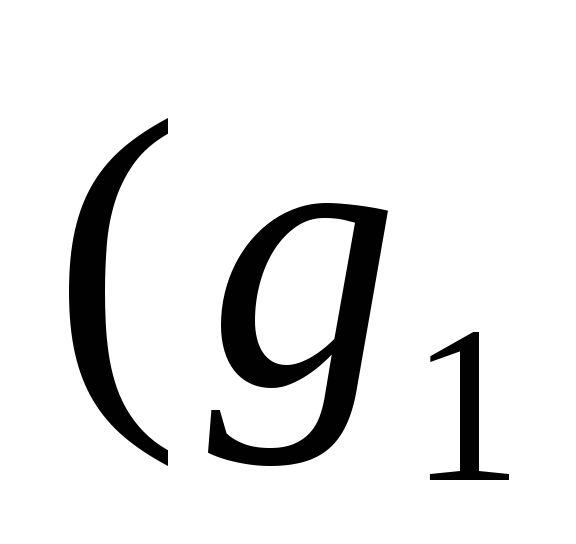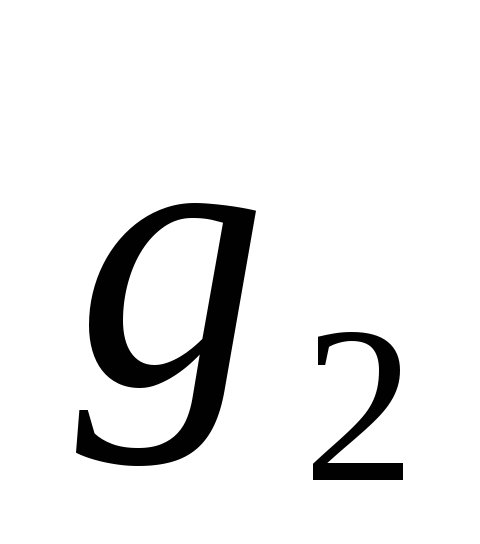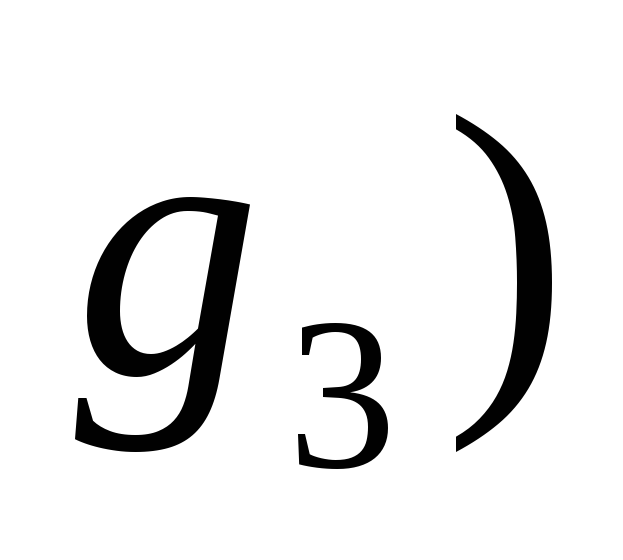существует e 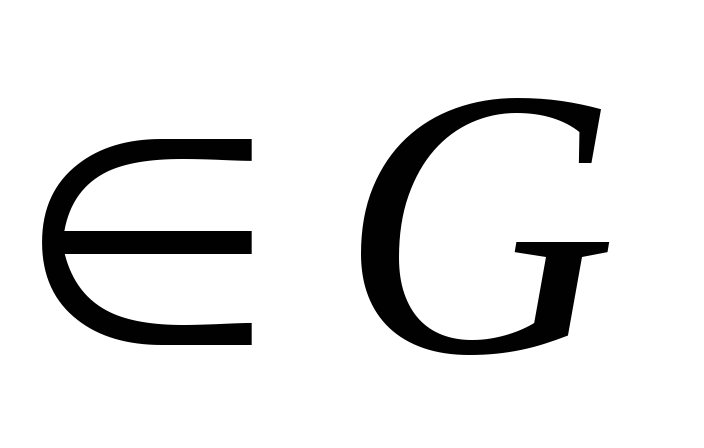: e•g=g•e=g

элемент e называется единицей группы G;

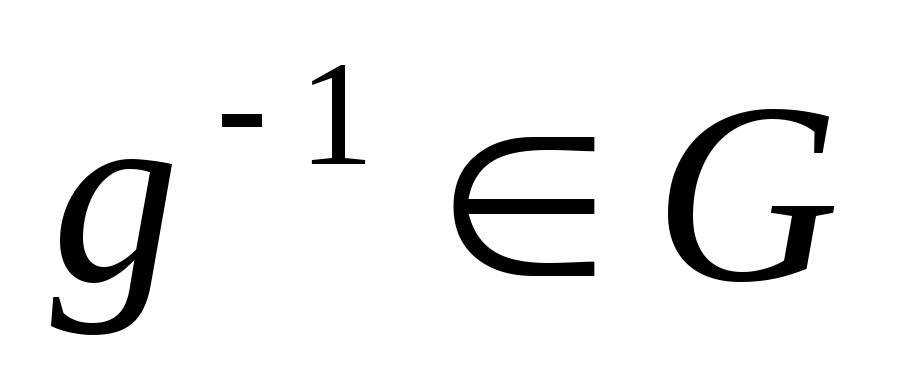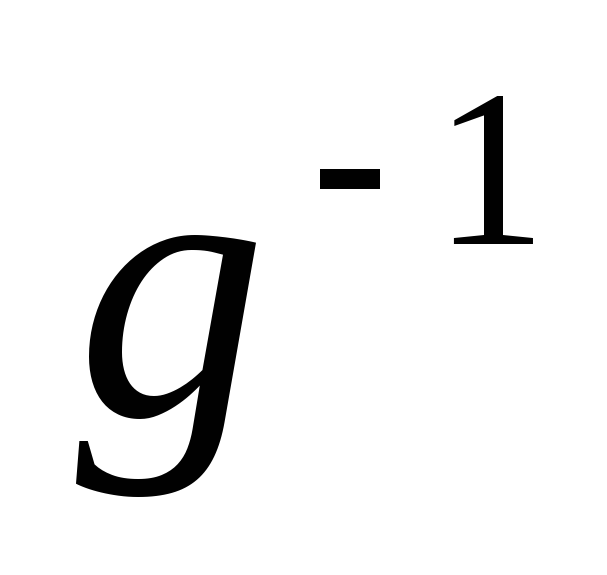для любого g существует элемент : g •=•g=e,

элемент для элемента g называется обратным к элементу g.

Если к условиям 1)-3) добавить условие

4) для любых •=•,

то группа G называется абелевой или коммутативной.

Группа содержит единственную единицу. Действительно, если два элемента обладают свойством 2) , то •.

В группе элемент, обратный к данному элементу g, может быть только один. Действительно, если два элемента и обладают свойством 3) для элемента g , то : •••=•=.

Определение. Пусть F –некоторая фигура на плоскости ,которую мы понимаем как множество точек.Движение плоскости f оставляет фигуру F на месте,если для любой точки AF точка f(A) также пренадлежит F.

Все движения плоскости оставляющие фигуру F на месте образуют группу движений этой фигуры.

Каждая конечная группа может быть задана таблицей умножения .Для составления таблицы умножения элементы группы вписываются по вертикали в определенном порядке .В клетке на пересечении строки и столбца пишется элемент .

Таблица умножения иногда называют “таблицей Кэли”.

Таблица Кэли обладает важным свойством: в каждой строке и в каждом столбце каждый элемент группы встречается ровно один раз. Таким образом каждый столбец и каждая строка являются некоторой перестановкой элементов группы.

Составим таблицу Кэли для группы движения правильного пятиугольника:

2.Подгруппы.

Определение.Подмножество H группы G ,само являющееся группой относительно операции,определяющей G т.е.:

для любых h и h которые принадлежат подмножеству H верно ,что

h(•) h принадлежит подмножеству H.

e принадлежит подмножеству H.

для любого элемента h принадлежащего подмножеству H верно ,что элемент h

принадлежит подмножеству H.

Подмножество группы G ,состоящие из одного элемента e будет подгруппой ,и эта подгруппа называется единичной подгруппой группы G и обозначается E.

Сама группа G также является, по определению , своей подгруппой.

Всякая подгруппа отличная от всей группы , называется истиной подгруппой.Группа G и подгруппа E называются несобственными(тривиальными) подгруппами группы G .Все остальные подгруппы –собственные подгруппы.

В группе всех движений правильного пятиугольника D нетривиальными подгруппами являются :

H={ e, ,,,},H={e,a},H={e,a,b},H={e,c},H={e,d},H={e,,d,f}

Определение.Число элементов группы или подгруппы называется ее порядком.

Если элемент а принадлежит группе G ,тогда наименьшее натуральное число такое ,что а=e называется порядком элемента а и обозначается о(а)=n.

Если таково n нет,то о(а)=∞.

Рассмотрим порядки элементов группы движений правильного пятиугольника D:

o(e)=1; о(a)=2; o(b)=2; o(c)=2; o(d)=2; o(f)=2; o()=5; o()=5; o()=5; o()=4;

Определение.Если H-подгруппа группы G и gG,то множество

называется левым смежным классом группы G по подгруппе H .Соответственно, множество Hg называется правым смежным классом.

Определение.Пусть а … а принадлежат G.Тогда будем обозначать < а… а> наимень-

шую подгруппу в G содержащую элементы а … а.Если <а … а> =G то элементы

{ а … а } будем называть системой образующих группы G .Cистему { а … а } будем называть минимальной системой образующих для G ,если после удаления любого элемента оставшееся множество уже не будет являться системой образующих для G .Группу G будем называть циклической,если найдется элемент G такой ,что G.

В группе движений правильного пятиугольника D минимальными системами образующих являются:

Так как группа движений правильного пятиугольника D не коммутативна (•,а •),она не может быть циклической.

По условию задания требуется составить таблицу умножения для группы из 12 элементов(e, a, a², a³, a⁴, a⁵, b, ab,a²b,a³b,a⁴b,a⁵b), исходя из условий, что a⁶=e, b⁴=e, ba=a⁵b, b²=a³