5.2.2 Способ свободной станции

Способ рассчитан на выполнение съемки электронным та­хеометром, установленным в произвольно выбранной съемоч­ной точке, не привязанной геодезическими измерениями к ка­ким-либо пунктам сети или другим съемочным точкам. Для определения площади способом свободной станции не требу­ется наличие геодезической сети.

Рис 5.5 Схема измерений на свободной станции

Э лектронный тахеометр устанавливают так, чтобы были видны все закрепляющие линию контура пикеты 1, 2, ...,n (на рис. 5.5 это точка А). Вешку с отражателем устанавливают в точках 1, 2, ..., n, фиксируя каждый раз горизонтальное рас­стояние d_i от съемочной точки А до очередного пикета i и отсчет М_i по горизонтальному кругу.

Направлениями из съемочной точки на пикеты вычисляе­мая площадь делится на секторы. Площади секторов вычис­ляют по формуле , (5.6)

где i – номер сектора; β_i = N_i+1 – N_i – острый угол треугольни­ка, вычисляемый как разность направлений на смежные пи­кеты i и i + 1.

Площадь всего участка найдем, суммируя площади сек­торов:

Р = Р₁ + Р₂ + ... + Р_n. (5.7)

Выше уже отмечено, что пикеты 1, 2, ..., n надо выбирать так часто, чтобы образуемая ломаная линия практически не отличалась от кривой.

Место для съемочной точки А может быть выбрано и вне ограничивающего площадь контура. Необходимость такого выбора может возникнуть, например, при определении пло­щади озера.

Искомая площадь Р (рис. 5.6) в этом случае равна разности площадей

Р = Р₁ – Р₂.

З

Рис. 5.6 Свободная станция вне контура участка

десьР₁ – сумма площадей секторов, ограниченных отрезками прямых от съемочной точ­ки А до точек 1, 2, 3, 4, 5, 6, 7, расположенных на дальней границе участка, и Р₂ – сумма площадей секторов, ограни­ченных отрезками прямых от съемочной точки А до точек 7, 8, 9, 10, 11, 1 на ближней границе участка.

Площадь каждого сектора вычисляется по формуле (5.6).

5.2.3 Способы нескольких свободных станций

Если с одной съемочной точки видны не все пикеты, рас­положенные на границе участка, можно выполнить определе­ние площади, используя несколько свободных станций.

Н

Рис. 5.7 Цепочка свободных станций

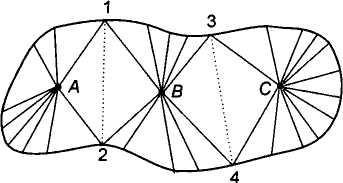а рис. 5.7 линиями 1-2 и 3-4, показанными пунктиром, участок разбит на три части, площадь каждой из которых оп­ределяется методом свободной станции, а именно тахеометрическими измерениями из пунктовА, В и С. Общая площадь участка равна сумме трех названных площадей.

На рис. 5.8 показана схема участка, значительная средняя часть которого недоступна для измерений (залесенность, за­стройка).

Рис. 5.8 Съемка площади с недоступной частью

Места для установки электронного тахеометра выбраны в точках А, В и С, связанных между собой только общими пике­тами 1, 2, 3. Площади, ограниченные границей контура и пунк­тирными линиями, проведенными через названные пикеты, мож­но вычислить, измерив показанные на схеме расстояния и го­ризонтальные направления на точки, аппроксимирующие криволинейную границу участка. При этом площади секторов определятся по формуле (5.6), а вся площадь, окружающая стан­цию (А, В или С), - по формуле (5.7). Например, площадь Р_А, окружающая пункт А, будет вычислена как сумма восьми сек­торов. Аналогично будут вычислены площади Р_В и Р_С.

Для вычисления площади треугольника 123 определим длины его сторон:

;

(5.8)

;

,

где β_А = ∟1А2, β_В = ∟2В3, β_С = ∟3С1. После чего площадь P_Δ треугольника определится по формуле (4.5), где а = d₁₂, b = d₁₃, c = d₂₃.

Площадь всего участка найдем, суммируя все четыре вы­численные площади: Р = Р_Δ + Р_А + Р_В + Р_С.